Give One Application Of P
P-N junction diodes are used as rectifiers in numerous electric circuits. They are also used as voltage-controlled oscillators in varactors.
Stay tuned with BYJUS to learn more physics concepts with the help of engaging video lessons.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
What Is $n$ In $e=nhf$ Is It The Number Of Photons Or Energy State Of Atom
I’ve been searching for the answer all over the internet, and all I found is two different answers and I need to know what answer is right.
1st answer
$E=nhf$ is an equation to find the ‘total energy’ for a group of photons in the same frequency for a single photon $E= hf$, is often expressed as $E= h\nu$ $n$ being the total number of photons. Because photons tend to travel in large groups, be better using this one: $$E = n\cdot N_A \cdot h\cdot f$$ In this equation $n$ is the number of moles, and $N_A$ is Avogadros number.
2nd answer
The $n$ refers to the nth state of vibration, $f$ is the frequency of the lowest energy state, $h$ is a constant called the Planck constant, and $E_n$ is the energy of the $n-$th level of vibration.
So who’s right?
What Is The Difference Between Balanced And Unbalanced Forces
Balanced forces have the same magnitude but opposite direction. They balance each other, and so cancel each other out. A classic example of balanced forces would be the gravitational force and the normal force acting on an object placed on a horizontal surface. Balanced forces cause no change in the direction or speed of an object.
Unbalanced forces don’t have the same magnitude. If an unbalanced force acts on an object, it impacts the object’s motion. For example, if something falls, it’s because of gravitational force. Air resistance force counteracts gravity, but it doesn’t balance it out if the object is too heavy.
Also Check: Formula To Find Half Life
Metric Units That Are Not Recognised By The Si
Although the term metric system is often used as an informal alternative name for the International System of Units, other metric systems exist, some of which were in widespread use in the past or are even still used in particular areas. There are also individual metric units such as the sverdrup and the darcy that exist outside of any system of units. Most of the units of the other metric systems are not recognised by the SI.
Here are some examples. The centimetregramsecond system was the dominant metric system in the physical sciences and electrical engineering from the 1860s until at least the 1960s, and is still in use in some fields. It includes such SI-unrecognised units as the gal, dyne, erg, barye, etc. in its mechanical sector, as well as the poise and stokes in fluid dynamics. When it comes to the units for quantities in electricity and magnetism, there are several versions of the CGS system. Two of these are obsolete: the CGS electrostatic ” rel=”nofollow”> statampere, etc.) and the CGS electromagnetic system ” rel=”nofollow”> maxwell, abhenry, gilbert, etc.). A ‘blend’ of these two systems is still popular and is known as the Gaussian system ” rel=”nofollow”> gauss as a special name for the CGS-EMU unit maxwell per square centimetre).
Overview Of The Units
SI base units
The SI selects seven units to serve as base units, corresponding to seven base physical quantities. They are the second, with the symbol s, which is the SI unit of the physical quantity of time the metre, symbol m, the SI unit of length kilogram ampere kelvin mole and candela . All units in the SI can be expressed in terms of the base units, and the base units serve as a preferred set for expressing or analysing the relationships between units.
SI derived units
The system allows for an unlimited number of additional units, called derived units, which can always be represented as products of powers of the base units, possibly with a nontrivial numeric multiplier. When that multiplier is one, the unit is called a coherent derived unit. The base and coherent derived units of the SI together form a coherent system of units . Twenty-two coherent derived units have been provided with special names and symbols. The seven base units and the 22 derived units with special names and symbols may be used in combination to express other derived units, which are adopted to facilitate measurement of diverse quantities.
Why SI kept the distinction between base and derived units
SI metric prefixes and the decimal nature of the SI
Like all metric systems, the SI uses metric prefixes to systematically construct, for the same physical quantity, a set of units that are decimal multiples of each other over a wide range.
Coherent and non-coherent SI units
New units
Recommended Reading: Mcdougal Littell Geometry Teacher Edition Answers
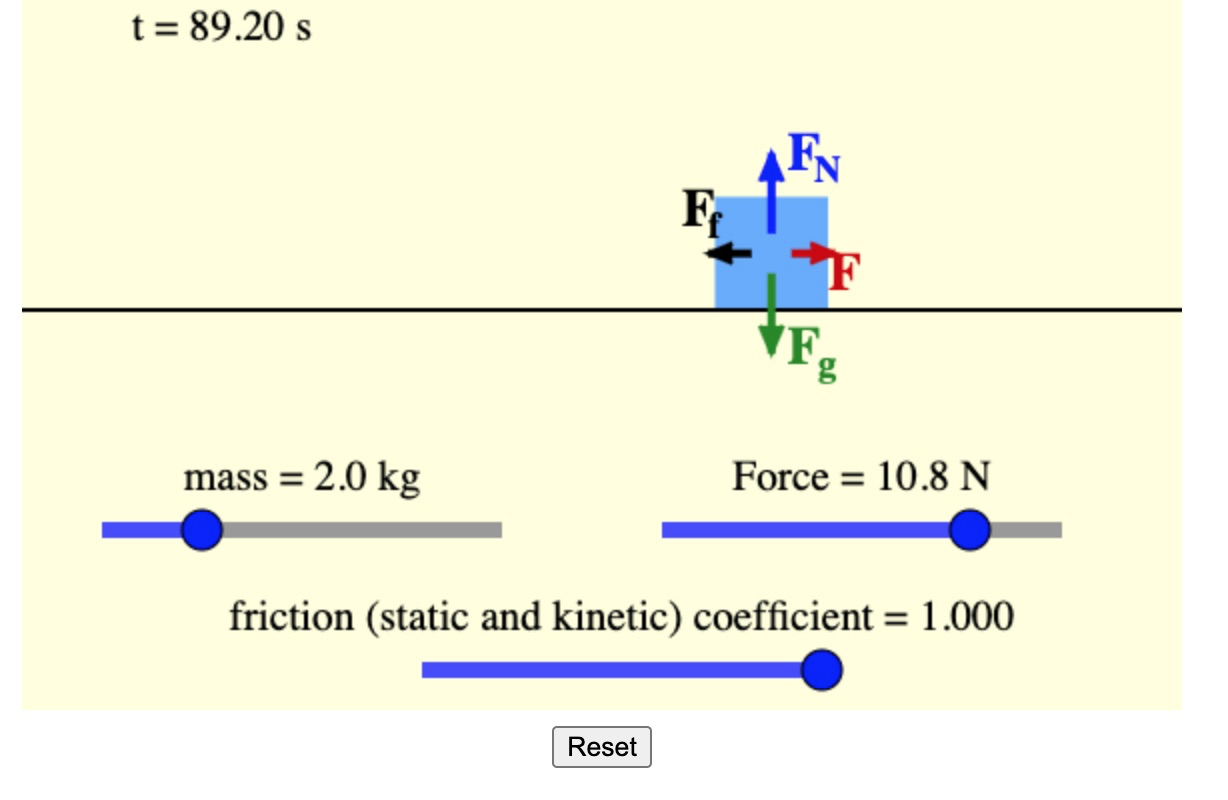
Force Definition And The Force Equation
What is force?
Force is any interaction that, if unopposed, can change the motion of an object.
If asked, “What is force?” a non-physicist would probably think about pushing and pulling. A physicist would think about the change in the velocity of an object. To understand why let’s look at the force equation:
- a is the acceleration of the object expressed in metre per second squared
- m is the mass of an object in kilograms and
- F is the force measured in Newtons .
Acceleration is the change of velocity over time. And, as you see from the force formula, the greater the force, the greater the acceleration. So, if something is speeding up, for example, a car, it can impart a significant force if it crashes on another car. This force is proportional to the car’s mass and its acceleration.
To use the force calculator, input two of these variables: mass, acceleration, or force in any unit and get the missing number in a blink of an eye.
If you’re calculating force on your own, always use the SI system to avoid mistakes. What is the SI unit of force? It’s Newton – named after Isaac Newton – mathematician, physicist, and discoverer of gravity. In SI base units, one Newton is equal to:
To learn more about force units go to our force converter.
International System Of Units
| 6.62607015×1034 Js | |
| e | |
|---|---|
| luminous efficacy of 540 THz radiation | 683 lm/W |
The International System of Units, known by the international abbreviation SI in all languages:125:iii and sometimes pleonastically as the SI system, is the modern form:117 of the metric system and the world’s most widely used system of measurement.:123 Established and maintained by the General Conference on Weights and Measures , it is the only system of measurement with an official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce.
The SI comprises a coherent system of units of measurement starting with seven base units, which are the second , metre , kilogram , ampere , kelvin , mole , and candela . The system can accommodate coherent units for an unlimited number of additional quantities. These are called coherent derived units, which can always be represented as products of powers of the base units. Twenty-two coherent derived units have been provided with special names and symbols.
Also Check: Sample Space Definition Math
Biasing Conditions For The P
There are two operating regions in the P-N junction diode:
- P-type
- N-type
There are three biasing conditions for the P-N junction diode, and this is based on the voltage applied:
- Zero bias: There is no external voltage applied to the P-N junction diode.
- Forward bias: The positive terminal of the voltage potential is connected to the p-type while the negative terminal is connected to the n-type.
- Reverse bias: The negative terminal of the voltage potential is connected to the p-type and the positive is connected to the n-type.
How To Calculate Force
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 30 people, some anonymous, worked to edit and improve it over time. This article has been viewed 1,273,522 times.Learn more…
Force is the “push” or “pull” exerted on an object to make it move or accelerate. Newton’s second law of motion describes how force is related to mass and acceleration, and this relationship is used to calculate force. In general, the greater the mass of the object, the greater the force needed to move that object.XResearch source
Also Check: Who Is Khloe Kardashian’s Real Father
The Discovery Of The Neutron Makes Z The Proton Number
All consideration of nuclear electrons ended with James Chadwick‘s discovery of the neutron in 1932. An atom of gold now was seen as containing 118 neutrons rather than 118 nuclear electrons, and its positive nuclear charge now was realized to come entirely from a content of 79 protons. Since Moseley had previously shown that the atomic number Z of an element equals this positive charge, it was now clear that Z is identical to the number of protons of its nuclei.
Newton’s Laws Of Motion
Newton came up with three laws of motion that explain the movement of all physical objects. They are the basics of all classical mechanics, which is also known as Newtonian mechanics.
An object will remain at rest or continue to move in uniform motion unless acted upon by an external force.
Force exerted by an object equals mass times acceleration of that object: F = m * a.
When one body exerts a force on a second body, the second body exerts a force equal in magnitude and opposite in direction on the first body .
Recommended Reading: Math Nation Independent Practice Answer Key
Commonly Seen As Kilonewtons
It is common to see forces expressed in kilonewtons , where 1 kN = 1000 N. For example, the tractive effort of a Class Y steam train locomotive and the thrust of an F100 jet engine are both around 130 kN.
One kilonewton, 1 kN, is equivalent to 102.0 kgf, or about 100 kg of load under Earth gravity.
- 1 kN = 102 kg × 9.81 m/s2.
So for example, a platform that shows it is rated at 321 kilonewtons , will safely support a 32,100-kilogram load.
Specifications in kilonewtons are common in safety specifications for:
- the holding values of fasteners, Earth anchors, and other items used in the building industry
- working loads in tension and in shear
The Cgs And Mks Systems

In the 1860s, James Clerk Maxwell, William Thomson and others working under the auspices of the British Association for the Advancement of Science, built on Gauss’s work and formalised the concept of a coherent system of units with base units and derived units christened the centimetregramsecond system of units in 1874. The principle of coherence was successfully used to define a number of units of measure based on the CGS, including the erg for energy, the dyne for force, the baryefor pressure, the poise for dynamic viscosity and the stokes for kinematic viscosity.
In 1879, the CIPM published recommendations for writing the symbols for length, area, volume and mass, but it was outside its domain to publish recommendations for other quantities. Beginning in about 1900, physicists who had been using the symbol “” for “micrometre” or “micron”, “” for “microlitre”, and “” for “microgram” started to use the symbols “m”, “L” and “g”.
In the late 19th and early 20th centuries, a number of non-coherent units of measure based on the gram/kilogram, centimetre/metre, and second, such as the Pferdestärke for power, the darcy for permeability and “millimetres of mercury” for barometric and blood pressure were developed or propagated, some of which incorporated standard gravity in their definitions.
Don’t Miss: Is Physics Easier Than Chemistry
Kinetic Theory Of Gases
Based on the primary assumptions that the volume of atoms or molecules is negligible, compared to the container volume and the attractive forces between molecules are negligible, the kinetic theory describes the properties of ideal gases. Here are the most important physics formulas related to the kinetic theory of monatomic gases.
Pressure = 1/3
Here, P is pressure, N is the number of molecules and v2 is the mean squared particle velocity.
Internal Energy = 3/2
Momentum And Energy Transformations In Relativistic Mechanics
Consider the same two frames as in case of Lorentz coordinate transformations above. S is moving at a velocity v along the x-axis. Here again is the Lorentz factor. In S frame and in S frame are momentum components. Now we consider formulas for momentum and energy transformations for a particle, between these two reference frames in relativistic regime.
Recommended Reading: Punchline Bridge To Algebra 2nd Ed Answers
The Proton And The Idea Of Nuclear Electrons
In 1915, the reason for nuclear charge being quantized in units of Z, which were now recognized to be the same as the element number, was not understood. An old idea called Prout’s hypothesis had postulated that the elements were all made of residues of the lightest element hydrogen, which in the Bohr-Rutherford model had a single electron and a nuclear charge of one. However, as early as 1907, Rutherford and Thomas Royds had shown that alpha particles, which had a charge of +2, were the nuclei of helium atoms, which had a mass four times that of hydrogen, not two times. If Prout’s hypothesis were true, something had to be neutralizing some of the charge of the hydrogen nuclei present in the nuclei of heavier atoms.
How Are Force And Motion Related
Force is any interaction that, if unopposed, can change the motion of an object. Without external force, a moving object will keep moving at a constant speed and direction, and an object at rest will stay at rest. If an external, unbalanced force is applied, an object will change the motion by changing its speed and/or direction.
The relationship between force and motion is defined by Newton’s laws of motion.
Don’t Miss: Jonathan Thomas Beth Thomas
Example 2 Soap Bubbles: More Than One Thickness Can Be Constructive
Strategy and Concept
nnn
Discussion
Physical Formulas For Quantities In Relativistic Dynamics
All the known quantities in classical mechanics get modified, when we switch over to relativistic mechanics which is based on the special theory of relativity. Here are formulas of quantities in relativistic dynamics.
Relativistic momentum p = m0v where m0 is the rest mass of the particle.
Rest mass energy E = m0c2
Total Energy E = )
Also Check: Equilateral Geometry Definition
The Practical System Of Units
In 1948, the 9th CGPM commissioned a study to assess the measurement needs of the scientific, technical, and educational communities and “to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention”. This working document was Practical system of units of measurement. Based on this study, the 10th CGPM in 1954 defined an international system derived from six base units including units of temperature and optical radiation in addition to those for the MKS system mass, length, and time units and Giorgi‘s current unit. Six base units were recommended: the metre, kilogram, second, ampere, degree Kelvin, and candela.
The 9th CGPM also approved the first formal recommendation for the writing of symbols in the metric system when the basis of the rules as they are now known was laid down. These rules were subsequently extended and now cover unit symbols and names, prefix symbols and names, how quantity symbols should be written and used, and how the values of quantities should be expressed.:104,130
The Periodic Table And A Natural Number For Each Element

Loosely speaking, the existence or construction of a periodic table of elements creates an ordering of the elements, and so they can be numbered in order.
Dmitri Mendeleev claimed that he arranged his first periodic tables in order of atomic weight . However, in consideration of the elements’ observed chemical properties, he changed the order slightly and placed tellurium ahead of iodine . This placement is consistent with the modern practice of ordering the elements by proton number, Z, but that number was not known or suspected at the time.
A simple numbering based on periodic table position was never entirely satisfactory, however. Besides the case of iodine and tellurium, later several other pairs of elements were known to have nearly identical or reversed atomic weights, thus requiring their placement in the periodic table to be determined by their chemical properties. However the gradual identification of more and more chemically similar lanthanide elements, whose atomic number was not obvious, led to inconsistency and uncertainty in the periodic numbering of elements at least from lutetium onward .
You May Like: Geometry Basics Unit 1 Answers