How To Do Elimination In Math

S For Solving Equations Through The Elimination Method

Lets look at how equations can be solved through the elimination method math step by step.

• If you get a true statement with no variable, then it means that the original equations have infinite solutions.

• If you get a false statement with no variable, then it means that the original equations do not have any solution and are inconsistent.

This will help you to solve the elimination method problems.

To make it Simpler for you, Consider the Following Example:

Solve this set of equations 2x + y = -4 and 5x 3y = 1 using elimination method..

The equations given are:;

Then the solution is x=5 and y=-1.

Two Ideal Cases Of The Elimination Method

I can summarize the big ideas about the elimination method when solving systems of linear equations using the illustrations below. Here I present two ideal cases that I want to achieve during the solving process. Take a look at them and hopefully, it makes sense. Otherwise, go directly to the six worked examples to see how actual problems are being solved.

Case 1: By Adding the Two Equations, the Variable x is Eliminated

The coefficients of variablex are opposites.

Case 2: By Adding the Two Equations, the Variable y is Eliminated

The coefficients of variabley are opposites.

What Is The Elimination Method In Algebra 1

In the elimination method you either add or subtract the equations to get an equation in one variable. When the coefficients of one variable are opposites you add the equations to eliminate a variable and when the coefficients of one variable are equal you subtract the equations to eliminate a variable.

Don’t Miss: When Was Geometry Dash Made

What Is The Formula Of Eliminate

The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation. So if you have a system: x 6 = 6 and x + y = 8, you can add x + y to the left side of the first equation and add 8 to the right side of the equation.

How To Solve Word Problems With The Elimination Method

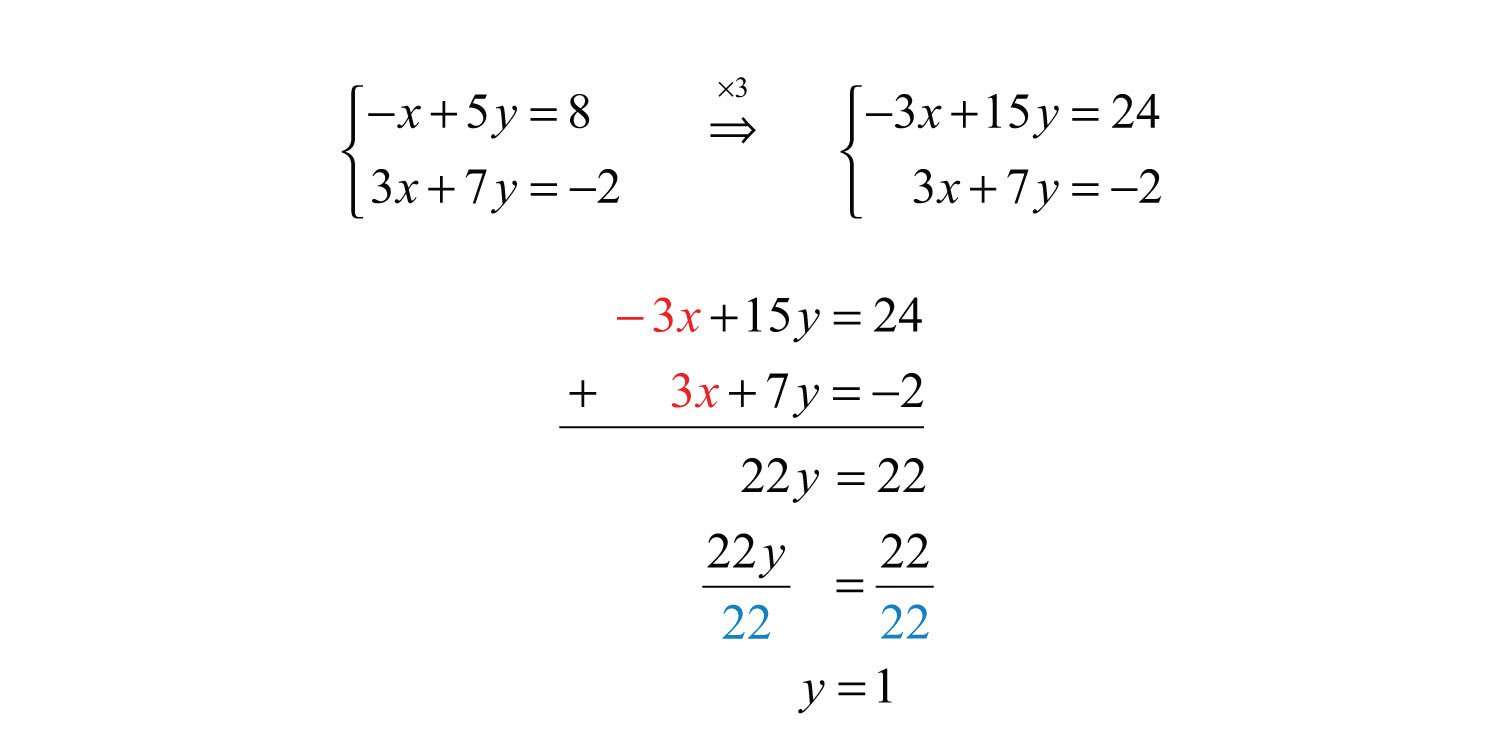
Suppose you are given a word problem without the equations. How do you solve the problem with the help of the elimination method? Well, the solution is simple. Take a look at the following example:

The charges of a park are \10 for adults and \5 for kids. How many adult tickets and kids tickets were sold if 548 tickets were sold for a total of \3750?

First step:

Consider the variable to x be the number of adult tickets and the variable y to be the number of kids tickets.

According to the problem, you can form two different equations.

x + y = 548 ———

Dividing both the sides by 5, you get,

2x + y = 750 ——–

Second step:

The next step is to eliminate one of the variables for getting the value of the other variable.

In the equations and , variable y is having the same coefficient. But it has the same sign in both the equations.;

For changing the sign of y in equation , multiply both sides of by the negative sign. This will give you,

– = – 548

– x – y = – 548 ——–

Third step:

Now, the step is eliminating the variable y in both the equations and as given below and finding the value of x. When you do so, you get,

2x + y = 750

__________

Fourth step:

Next, substitute the value 202 for x in equation to get the value of the variable y. After doing so, you get,

202 + y = 548;

Subtracting 202 from both the sides, you get,;

y = 346

Therefore, the number of tickets sold for adults is 202 and the number of tickets sold for kids is 346.

1. What is Elimination Method?

x – y = -6

Read Also: How Do You Find The Difference In Math

How To: Given A System Of Equations Solve Using The Elimination Method

How Do You Solve An Equation With 2 Variables

In a two- variable problem rewrite the equations so that when the equations are added, one of the variables is eliminated, and then solve for the remaining variable. Step 1: Multiply equation by -5 and add it to equation to form equation with just one variable.

You May Like: What Is Energy In Quantum Physics

S To Use Elimination Method

The elimination method is useful to solve linear equations containing two or three variables. We can solve three equations as well using this method. But it can only be applied to two equations at a time. Let us look at the steps to solve a system of equations using the elimination method.

• Step-1: The first step is to multiply or divide both the linear equations with a non-zero number to get a common coefficient of any one of the variables in both equations.
• Step-2: Add or subtract both the equations such that the same terms will get eliminated.
• Step-3: Simplify the result to get a final answer of the left out variable such that we will only get an answer in the form of y=c, where c is any constant.
• Step-4: At last, substitute this value in any of the given equations to find the value of the other given variable.

These are the elimination method steps to solve simultaneous linear equations. Let us take an example of two linear equations x+y=8 and 2x-3y=4 to understand it better.

Let, x+y=8 ___ and 2x-3y=4 ___

Step 1: To make the coefficients of x equal, multiply equation by 2 and equation by 1. We get,

× 2 ___

× 1 ___

So, the two equations we have now are 2x+2y=16 __ and 2x-3y=4 __ .

Step 2: Subtract equation 2 from 1, we get, y=12/5.

Step 3: Substitute the value of y in equation 1, we get, x + 12/5 = 8

x = 8 – 12/5

x = 28/5

Therefore, x = 28/5 and y=12/5.

How Do You Solve Linear Equations Using The Elimination Method

Simultaneous linear equations can be solved using the elimination method. First of all, make sure that the equations are written in the standard form either Ax+By=C or Ax+By+C=0. In this method, we multiply both the equations with a non-zero number to make the coefficients of any one variable equal. Then we add or subtract the equations to eliminate one of the variables to find the value of the other variable. This is how we solve linear equations by the elimination method.

Don’t Miss: What Is Standardization In Chemistry

How To Solve A System Using The Elimination Method

Example

To solve the system by elimination, what would be a useful first step?

???x+3y=12???

???2x-y=5???

When we use elimination to solve a system, it means that were going to get rid of one of the variables. So we need to be able to add the equations, or subtract one from the other, and in doing so cancel either the ???x???-terms or the ???y???-terms.

Any of the following options would be a useful first step:

Multiply the first equation by ???-2???;or ???2???. This would give us ???2x???;or ???-2x???;in both equations, which will cause the ???x???-terms to cancel when we add or subtract.

Multiply the second equation by ???3???;or ???-3???. This would give us ???3y???;or ???-3y???;in both equations, which will cause the ???y???-terms to cancel when we add or subtract.

Divide the second equation by ???2???. This would give us ???x???;or ???-x???;in both equations, which will cause the ???x???-terms to cancel when we add or subtract.

Divide the first equation by ???3???. This would give us ???y???;or ???-y???;in both equations, which will cause the ???y???-terms to cancel when we add or subtract.

Lets re-do the last example, but instead of the elimination method, use a graph to find the solution.

How Do You Solve By Elimination

The Elimination Method

Don’t Miss: Which Founding Contributors To Psychology Helped Develop Behaviorism

Solving Linear Equations By Elimination Method

The elimination method is one of the techniques to solve the system of linear equations. In this method, either add or subtract the equations to get the equation in one variable. If the coefficients of one of the variables are the same, and the sign of the coefficients are opposite, we can add the equation to eliminate the variable. Similarly, if the coefficients of one of the variables are the same, and the sign of the coefficients are the same, we can subtract the equation to get the equation in one variable.

In case, if we do not have the equation to directly add or subtract the equations to eliminate the variable, you can begin by multiplying one or both the equations by a constant value on both sides of an equation to obtain the equivalent linear system of equations and then eliminate the variable by simply adding or subtracting equations.

Also, read:

Can The Elimination Method Be Used To Solve The System Of Equations In Three Variables

Yes, the elimination method can be used to solve linear equations with three variables. With three equations, we take any two equations and select the variable to be eliminated. Then we repeat the same process by taking another pair of equations and eliminate the same variable. In this way, we will be left with two equations in two variables only that can be solved using the elimination method. At last, we put the values of those two variables in any of the given equations to find the value of the third variable.

Read Also: What Is Copulation In Biology

Solve A System Of Equations When Multiplication Is Necessary To Eliminate A Variable

Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.

\begin3x+4y=52\\5x+y=30\end

If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So lets now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will allow you to eliminate;the same variable in the other equation.

We do this with multiplication.;;Notice that the first equation contains the term 4y, and the second equation contains the term y. If you multiply the second equation by 4, when you add both equations the y variables will add up to 0.

The following example takes you through all the steps to find a solution to this system.

Answer

The solution is .

Elimination Method: Infinitely Many Solutions

Two equations of coincident lines have infinitely many solutions possible. So, if by the elimination method we solve a system of equations of coincident lines, we get a consistent system with infinite solutions. In such cases, we get an answer in the form of 0=0 if we apply the elimination method. For example, try to solve equations x+y=2 and 2x+2y-4=0. If you multiply any non-zero constant with both equations, you will find that every time x-variable terms and y-variable terms are getting canceled or eliminated. So, in the elimination method when there are infinitely many solutions possible, we get the result in the form of 0=0. It is advisable to check whether the given linear equations are of intersecting lines, parallel lines, or coincident lines before trying to solve them. Check this article to know about the solutions of linear equations.

Also Check: Geometry Lesson 1.7 Answers

Elimination Method: No Solutions

As we know that equations of two parallel lines have no solutions. So, if we solve any such equations using the elimination method we get the answer as two unequal numbers on both sides of the unequal sign. For example, 08, -20, etc. In such cases, we cannot eliminate only one variable. Both the variables get eliminated. For example, let us solve two equations 2x-y=4 __ and 4x-2y=7 __ by the elimination method. In order to make the x coefficients equal in both the equations, we multiply equation by 2 and equation by 1. By doing so we get, 4x-2y=8 __ and 4x-2y=7 __ . Now, if we try to subtract equation 4 from equation 3, we get, 0=1 as both the variables are getting eliminated. There is no other way to solve these equations as the solutions are inconsistent. So, in the elimination method when there is no solution, we get the result in this form.

What Are The Steps Involved In The Elimination Method

The steps involved in the elimination method are given below:

• Choose any one variable to eliminate. Multiply or divide both the equations with a non-zero constant to make the coefficients of that variable equal.
• Add or subtract the resultant equations such that the chosen variable gets eliminated.
• Simplify and find the value of the other variable.
• Substitute that value in any of the given equations to find the value of the eliminated variable.

You May Like: What Does Abiotic Mean In Biology

How Do You Know When To Use Elimination Or Substitution

If the coefficient of any variable is 1, which means you can easily solve for it in terms of the other variable, then substitution is a very good bet. If all the coefficients are anything other than 1, then you can use elimination, but only if the equations can be added together to make one of the variables disappear.

Solve Systems Of Equations By Elimination

• Publisher: OpenStax CNX

• Solve a system of equations by elimination
• Solve applications of systems of equations by elimination
• Choose the most convenient method to solve a system of linear equations

Note

Before you get started, take this readiness quiz.

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what well do with the elimination method, too, but well have a different way to get there.

Also Check: Why Biology Is The Best Science

How Do You Do Elimination With 3 Variables

To use elimination to solve a system of three equations with three variables, follow this procedure:

Solving A Set Of Linear Equations By The Elimination Method

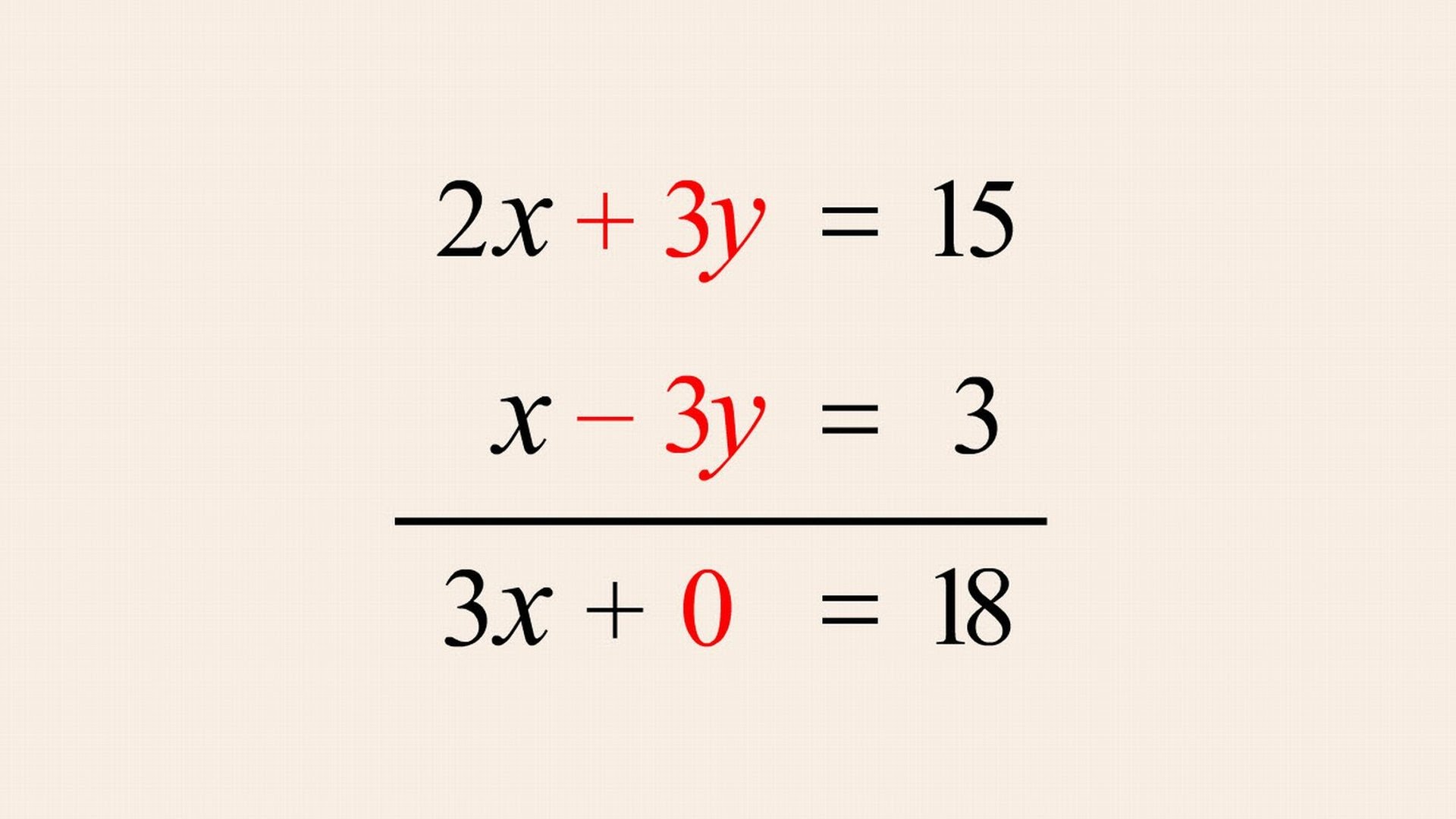
For solving the simultaneous linear equations, you reduce the pair of the equations to one linear equation in one variable. You then solve it normally. Solving equations through the elimination method would require you to multiply the coefficients of the given equations and make the coefficients of one variable the same amongst both the equations. Lastly, just one variable would remain in the end which you can solve easily. Given below are the steps to solve by elimination method.

Recommended Reading: What Is E Called In Math

Is The Addition Method The Same As Elimination

Solving Systems of Equations in Two Variables by the Addition Method. A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero.

Systems Of Linear Equations:

A system of is just a set of two or more linear equations.

In two variables y ) , the graph of a system of two equations is a pair of lines in the plane.

There are three possibilities:

• The lines intersect at zero points.
• The lines intersect at exactly one point.
• The lines intersect at infinitely many points.

How to Solve a System of Linear Equations Using The Elimination Method

• Step 1 : Add a multiple of one equation to the other equation, in such a way that either the x
• y , whichever’s left) and substitute back to get the other coordinate.

Now, how do we know that a linear equation obtained by the addition of the first equation with a scalar multiplication of the second is equivalent to the first?

Let us take an example. Consider the system

Consider the equation obtained by multiplying the second equation by a constant m and then adding the resultant equation with the first one.

That is,

What we need to prove is that this equation is equivalent to the equation 3

from the left side and from the right side of the equation ( which will retain the balance.

Cancelling common terms we get, 3 which is equivalent to the first equation.

Therefore, the systems of equations 3

In general, for any system of equations K , it ca be shown that K

Multiply the first equation by and add the result to the second equation.

in either of the original equations and solve for x

Don’t Miss: How Do Noise Cancelling Headphones Work Physics