What Are The Different Kinds Of Reasoning In Geometry

What Is Logical Reasoning Geometry

Logical reasoning is a useful tool in many areas, including solving math problems. Logical reasoning is the process of using rational, systemic steps, based on mathematical procedure, to arrive at a conclusion about a problem. You can draw conclusions based on given facts and mathematical principles.

As A Description Of The Structure Of Space

Euclid believed that his axioms were self-evident statements about physical reality. Euclid’s proofs depend upon assumptions perhaps not obvious in Euclid’s fundamental axioms, in particular that certain movements of figures do not change their geometrical properties such as the lengths of sides and interior angles, the so-called Euclidean motions, which include translations, reflections and rotations of figures. Taken as a physical description of space, postulate 2 asserts that space does not have holes or boundaries; postulate 4 says that space is isotropic and figures may be moved to any location while maintaining congruence; and postulate 5 that space is flat .

As discussed in more detail below, Albert Einstein‘s theory of relativity significantly modifies this view.

The ambiguous character of the axioms as originally formulated by Euclid makes it possible for different commentators to disagree about some of their other implications for the structure of space, such as whether or not it is infinite and what its topology is. Modern, more rigorous reformulations of the system typically aim for a cleaner separation of these issues. Interpreting Euclid’s axioms in the spirit of this more modern approach, axioms 1-4 are consistent with either infinite or finite space , and all five axioms are consistent with a variety of topologies .

Analogical Reasoning Explained With Examples

Analogical reasoning is reasoning from the particular to the particular . It is often used in case-based reasoning, especially legal reasoning.

Ex 1.

• Premise 1: Socrates is human and mortal.
• Premise 2: Plato is human.

Since Socrates is human and mortal, and since Plato is human, it stands to reason that Plato is also mortal.

This is a sort of inductive reasoning that produces weak arguments in many cases due to its structure. Consider the next example which produces an invalid result.

Ex 2.

• Premise 1: Socrates is human and male.
• Premise 2: Cleopatra is human.

Just because Socrates has two properties and shares one with Cleopatra doesnt mean he shares all properties with Cleopatra, if he did, he wouldnt be the unique person Socrates, he would be a categorical term.

Don’t Miss: Pre Algebra Order Of Operations Help

Deductive Reasoning Explained With Examples

Deductive reasoning;is the process of reasoning from one or more statements to reach a logically certain conclusion . This sort of reasoning results in absolute truth-values.

Ex 1.

1. 25% of beans are red, 2. 75% are blue, 3. the bag has a mix of beans of different types, 4. therefore there are red and blue beans in the bag.

We deduced that the bag must contain both red and blue beans for sure given the facts.

Ex 2.

• Premise 1: All humans are mortal.
• Premise 2: All Greeks are human.

Since all Greeks alive today are human , we can know with 100% certainty that all Greeks are mortal .

TIP: Deductive reasoning can also be probable, this is because it is only certain when the argument is 100% valid. If we were unaware of an immortal Greek, then our conclusion would be false, even though our logic was sound. If our logic isnt sound . One can arrive at a true conclusion using unsound logic and invalid reasoning by luck, but that is not the main point here.

Th Century And Relativity

Einstein’s theory of special relativity involves a four-dimensional space-time, the Minkowski space, which is non-Euclidean. This shows that non-Euclidean geometries, which had been introduced a few years earlier for showing that the parallel postulate cannot be proved, are also useful for describing the physical world.

However, the three-dimensional “space part” of the Minkowski space remains the space of Euclidean geometry. This is not the case with general relativity, for which the geometry of the space part of space-time is not Euclidean geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees due to gravity. A relatively weak gravitational field, such as the Earth’s or the Sun’s, is represented by a metric that is approximately, but not exactly, Euclidean. Until the 20th century, there was no technology capable of detecting these deviations in rays of light from Euclidean geometry, but Einstein predicted that such deviations would exist. They were later verified by observations such as the slight bending of starlight by the Sun during a solar eclipse in 1919, and such considerations are now an integral part of the software that runs the GPS system.

You May Like: What Does I Stand For In Physics

Why Does My Brain Not Understand Math

We have recently recognised a condition in the brain called dyscalculia, which is for numbers what dyslexia is for words. It’s a learning difficulty that makes it difficult to process numbers and perform arithmetical tasks. … It’s thought that about 5% of the population may have some degree of dyscalculia.

Iv The History And Importance Of Logical Reasoning

Logic is a universal part of the human experience agriculture would be impossible without inductive reasoning about weather and sunlight, and construction would be impossible without mathematics and deductive reasoning about what makes a structure sturdy.

Formalized logic has appeared in several places with more or less similar results. The Greek philosopher Aristotle is credited with being the first to develop a formal system of logical reasoning, but there were already people in India and China working on formal logic long before Aristotle was born. The Indian, Chinese, and Greek systems were all remarkably similar in their rules, which suggests that there may have been some mutual influence despite the distance. Traders and travelling scholars may have brought ideas about logical reasoning with them all over the world, allowing for rapid development of new ideas.

Logic may seem like a stuffy, abstract discipline used only by philosophers and lawyers, but it has had a profound influence on the history of science and technology as well. Alan Turing, the inventor of the modern computer, was a logician rather than a tinkerer or engineer, and his famous Turing Machine was a product of his rigorous training in formal logical reasoning.

Recommended Reading: What Is Biomass In Biology

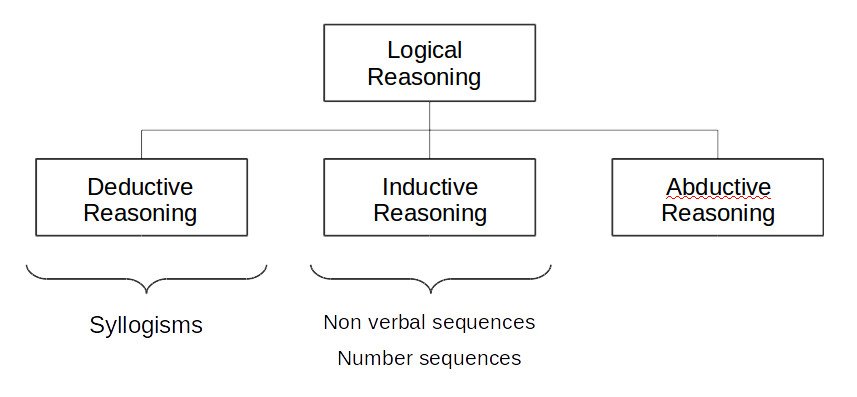
Types Of Reasoning In Maths

In terms of mathematics, reasoning can be of two major types which are:

The other types of reasoning are intuition, counterfactual thinking, critical thinking, backwards induction and abductive induction. These are the 7 types of reasoning which are used to make a decision. But, in mathematics, the inductive and deductive reasoning are mostly used which are discussed below.

Note: Inductive reasoning is non-rigorous logical reasoning and statements are generalized. On the other hand, deductive reasoning is rigorous logical reasoning, and the statements are considered true if the assumptions entering the deduction are true. So, in maths, deductive reasoning is considered to be more important than inductive.

Examples Of Logic: 4 Main Types Of Reasoning

In simple words, logic is the study of correct reasoning, especially regarding making inferences. Logic began as a philosophical term and is now used in other disciplines like math and computer science. While the definition sounds simple enough, understanding logic is a little more complex. Use logic examples to help you learn to use logic properly.

Don’t Miss: Geometry Dash Practice Song Hack

Scaling Of Area And Volume

In modern terminology, the area of a plane figure is proportional to the square of any of its linear dimensions, A 3 } . Euclid proved these results in various special cases such as the area of a circle and the volume of a parallelepipedal solid. Euclid determined some, but not all, of the relevant constants of proportionality. E.g., it was his successor Archimedes who proved that a sphere has 2/3 the volume of the circumscribing cylinder.

Synthetic Reasoning Explained With Examples

Synthetic reasoning is a form of reasoning where one compares the difference and similarities between propositions and attempts to synthesize them to draw an inference . It is essentially a hybrid form of analogical and abductive reasoning.

Ex 1.

• Conclusion: Perhaps the political left and right are naturally occurring and are a reflection of the archetype male and female ?

And with that we have grounds to formulate a hypothesis and begin the process of speculation. Here our hypothesis is based on the synthesis of two ideas. Thus, synthetic reasoning is really just a flavor of abduction.

Ex 2.

• Premise 1: All humans are mortal.
• Premise 2: All Greeks are human.
• Synthetic Reasoning: But wait, oddly we find that the flat worm is , so what if there is a sub-class of humans who break this rule under special circumstances? < Again, with that we have grounds to formulate a hypothesis and begin the process of speculation.

In other words,;synthetic reasoning is just a term that speaks to looking at the spaces in between, the relations of things. It could easily be considered as a part of induction and abduction and is generally talked about alongside abduction, or even as a synonym for abduction, if at all.

NOTE: Synthetic reasoning is not widely accepted as a form of reasoning.

Also Check: How Do Noise Cancelling Headphones Work Physics

What Is Mathematical Reasoning

Mathematical reasoning is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman’s words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual’s opinion. Derivations and proofs require a factual and scientific basis.;

Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.;

When we learn literature, we follow certain rules of grammar. Likewise, there are certain rules and parts of a scientific hypothesis. It is important to note that most books and texts written on mathematical reasoning follow scientific grammar or relevant terminologies and notations.

Sample Mathematical Reasoning Questions With Answers

Now that we have an understanding of Mathematical Reasoning and the various terminologies and reasoning associated, we will go through two sample questions with an explanation to understand maths and reasoning in depth.

Q1. Look at this series: 12, 10, 13, 11, 14, 12, What number should come next?

A. 15

D. CIRCUMFERENCE

Answer: D.CIRCUMFERENCE.;

Explanation:;The boundary of a square is given by its perimeter just as the boundary of a circle is given by circumference.

Most kids study mathematics for the sake of grades. That will improve grades temporarily but cause great damage in the longer run. Kids need to ask questions to understand how a particular concept is being used. If children do not understand the concepts in their initial days, they will struggle at a later stage.

You May Like: What Is Energy In Quantum Physics

What Did Egyptians Invent

Therefore, the Egyptians had to invented mathematics, geometry, surveying, metallurgy, astronomy, accounting, writing, paper, medicine, the ramp, the lever, the plough, mills for grinding grain and all the paraphernalia that goes with large organised societies. So how do we define Egyptian inventions today?

Comparing Induction And Deduction To Illustrate The Basics

Consider the following deductive argument consisting of an if..then statement as the major premise, an observation as the second premise, and a logical conclusion .

Deduction Ex. Premise 1: If its raining then its cloudy. Premise 2: Its raining. Conclusion: Its cloudy.

That above argument is deductive, because it deduced a necessarily certain truth that logically and necessarily followed from the premises .

Now lets make that same argument inductive.

Induction Ex. Premise 1: If its raining then its probably cloudy. Premise 2: Its raining. Conclusion: Its probably cloudy.

That argument is inductive, because it deduced a probable truth from premises that contained probable truth even though the conclusion didnt necessary follow the premises .

Now, lets make that same argument abductive.

Abduction Ex. Premise 1: Its raining. Premise 2: Its cloudy. Conclusion: Perhaps if its raining then its likely cloudy as a general rule?

That argument is abductive, because it outputs a hypothesis rather than a likely or certain conclusion.

Above we could have made both of the deductive premises about universally true rules , and for the inductive argument we could have used two or more probable rules and/or facts about specific things. Likewise, we could have compared any interesting observation with a probable or certain rule or another observation and formulated a hypothesis in our abduction example.

Here are other examples of what the above arguments could look like:

Don’t Miss: What Is Gradualism In Biology

Abductive Reasoning Explained With Examples

Abductive reasoning is like educated guessing or reasoning by hypothesis. In other words, abductive reasoning is a form of inductive reasoning which starts with an observation then seeks to find the simplest and most likely explanation . The reason it is distinguished from inductive reasoning is because it tries to find the best conclusion by attempting to falsify alternative explanations or by demonstrating the likelihood of the favored conclusion.;Abductive reasoning is one reasoning method used in the scientific method .

Ex 1.

1. there is a bag with 1,000 beans in it which are either 99% red and 1%blue or 1% red and 99% blue, 2. we randomly pull out ten beans and they are all blue 3. therefore it is very likely that the bag contains 1% red and 99% blue beans.

We hypothesized that this was the bag with mostly blue beans because we pulled 10 beans from the bag at random, and that would have been very unlikely if only 1% of the thousand beans in the bag were blue.

Ex 2.

The surprising fact, C, is observed;

But if A were true, C would be a matter of course,

Hence, there is reason to suspect that A is true.

Ex 3.

Socrates didnt die like the rest of the Greeks;

If some Greeks werent mortal, this could explain why Socrates didnt die,

Hence, we can can suspect that not all humans are mortal.

Here;the hypothesis is framed, but not asserted, in a premise, then asserted as rationally suspect-able in the conclusion.

Why Is Mathematical Reasoning Important

Students have the potential to solve higher-order thinking questions which are frequently asked in competitive examinations. But a lack of mathematical reasoning skills may render their potential. Encouragement is needed to develop a student’s natural inclination to strive for purpose and meaning.

The reasoning is the most fundamental and essential tool of mathematics. It helps one understand and justify mathematical theorems. A good grip in reasoning will help students apply the concepts they learn in the classroom.;

You May Like: What Is Copulation In Biology

More On Abductive Reasoning

As noted above, the rest of the reasoning types are essentially names for specific forms, flavors, or mixes of deduction and induction .

Of these forms, flavors, and mixes the most notable is;abductive reasoning. Abductive reasoning is defined simply as finding the best explanation for a given observation.

In other words, abduction speaks to conceptualizing a speculative hypothesis based on an interesting observation using guesswork.

Here is one way to illustrate the difference between deduction, induction, and abduction, this time using the terms rule, case, and fact to describe the parts of the argument .

TIP: Abduction is all about generating a hypothesis, that hypothesis can then be checked via induction .

Rule, Case, Fact: Above we used the terms rule , case , fact . From this perspective, the reasoning types are at least partly defined by where rules, cases, and facts appear in the conclusions or premisses . With that in mind, abductive reasoning is unique because it tries to connect an observation with a general rule to formulate a hypothesis about what could have happened in this case. Abductive is therefore like a mix or bridge between deductive and inductive reasoning . To help wrap your mind around the difference between these three, see;an interesting take on the matter from;inquiryintoinquiry.com.

The Laws Of Thought And Probability

The general rules behind;the nature of what we can know by deductive reasoning are reducible to a;few;axioms, these are;the;Classical Three Fundamental Laws of Thought. To this we only need to add the laws of probability to have the general rules behind what we can know through any reasoning method.

Read Also: What Does Abiotic Mean In Biology

Deductive Reasoning Vs Inductive Reasoning

The structure of a syllogism works for both inductive and deductive arguments, but these two types have a key difference.

Deductive reasoning produces constant truth-values, inductive doesnt .

With that in mind, an inductive syllogism might look like this:

With deductive reasoning we can know whether an argument is true or not based on figure . That means we can create a logic rule-set that always works.

It doesnt work the same way with inductive reasoning .

In other words, there are different metrics that apply to deductive and inductive reasoning respectively. So lets cover those now to further illustrate the difference between these two main logic types.