What Is E Called In Math

What About Different Rates

Good question. What if we grow at 50% annually, instead of 100%? Can we still use e?

Lets see. The rate of 50% compound growth would look like this:

Hrm. What can we do here? Remember, 50% is the total return, and n is the number of periods to split the growth into for compounding. If we pick n=50, we can split our growth into 50 chunks of 1% interest:

Sure, its not infinity, but its pretty granular. Now imagine we also divided our regular rate of 100% into chunks of 1%:

Ah, something is emerging here. In our regular case, we have 100 cumulative changes of 1% each. In the 50% scenario, we have 50 cumulative changes of 1% each.

What is the difference between the two numbers? Well, its just half the number of changes:

This is pretty interesting. 50 / 100 = .5, which is the exponent we raise e to. This works in general: if we had a 300% growth rate, we could break it into 300 chunks of 1% growth. This would be triple the normal amount for a net rate of $e^3$.

Even though growth can look like addition , we need to remember that its really a multiplication . This is why we use exponents and square roots .

Although we picked 1%, we could have chosen any small unit of growth . The key is that for any rate we pick, its just a new exponent on e:

Common Mathematical Symbols And Terminology: Maths Glossary

Mathematical symbols and terminology can be confusing and can be a barrier to learning and understanding basic numeracy.

This page complements our numeracy skills pages and provides a quick glossary of common mathematical symbols and terminology with concise definitions.

Are we missing something? Get it touch to let us know.

Example: How Many Different Ways Can 7 People Come 1st 2nd And 3rd

The list is quite long, if the 7 people are called a,b,c,d,e,f and g then the list includes:

abc, abd, abe, abf, abg, acb, acd, ace, acf, … etc.

The formula is 7!! = 7!4!

Let us write the multiplies out in full:

7 × 6 × 5 × 4 × 3 × 2 × 14 × 3 × 2 × 1; = ;7 × 6 × 5

That was neat. The 4 × 3 × 2 × 1 “cancelled out”, leaving only 7 × 6 × 5. And:

7 × 6 × 5; = ;210

There are 52! ways to shuffle a deck of cards.

That is 8.0658175… × 1067

Just shuffle a deck;of cards and it is likely that you are the first person ever with that particular order.

There are about 60! atoms in the observable Universe.

60! is about 8.320987… × 1081 and the current estimates are between 1078 to 1082 atoms in the observable Universe.

70! is approximately 1.197857… x 10100, which is just larger than a Googol .

100! is approximately 9.3326215443944152681699238856 x 10157

200! is approximately 7.8865786736479050355236321393 x 10374

Recommended Reading: What Is Gradualism In Biology

Ways To Express Eulers Number

Since Eulers number is irrational, there is no way to express it as a fraction of integers, or as a finite or periodic decimal number. It comes up so often in both pure and applied math, however, there are many other ways it can be expressed. Some of these include:

for any real number x, or.Or using limits:Or as a sum of trig functions:

Derivatives And Differential Equations

PhbxPhhb

The importance of the exponential function in mathematics and the sciences stems mainly from its property as the unique function which is equal to its derivative and is equal to 1 when x = 0. That is,

d 1. }e^=e^\quad }\quad e^=1.}

Functions of the form cex for constant c are the only functions that are equal to their derivative . Other ways of saying the same thing include:

• The slope of the graph at any point is the height of the function at that point.
• The rate of increase of the function at x is equal to the value of the function at x.
• The function solves the differential equationy = y.
• exp is a fixed point of derivative as a functional.

If a variable’s growth or decay rate is proportional to its sizeas is the case in unlimited population growth , continuously compounded interest, or radioactive decaythen the variable can be written as a constant times an exponential function of time. Explicitly for any real constant k, a function f: R R satisfies f = kf if and only if f = cekx for some constant c. The constant k is called the , disintegration constant,rate constant, or transformation constant.

Furthermore, for any differentiable function f, we find, by the chain rule:

d

t 0 ^}|\gamma ‘|dt=\int _^}|i\exp|dt=t_} ,

The complex exponential function is periodic with period 2i and exp

The third and fourth images show how the graph in the second image extends into one of the other two dimensions not shown in the second image.

) b =\left^=\left^=e^}

You May Like: Exponential Growth And Decay Common Core Algebra 1 Homework Answers

What Is The Value Of E In Maths

As discussed earlier, Jacob Bernoulli discovered the mathematical constant e. The expression, given as the sum of infinite for Eulers constant, e, can also be expressed as;

Therefore, the value of n reaches e when n reaches . If we put the value of n in the above expression, we can calculate the approximate the number e value. So, lets start putting the value of n =1 to higher digits.

e = 1/1 + 1/1 + 1/2+ 1/6 + 1/24 + 1/120 +

Now, taking the first few terms only.

e = 1/1 + 1/1 + 1/2+ 1/6 + 1/24 + 1/120

e = 2.71828

Therefore, the value of e is equal to 2.71828 or e 2.72.

Learn more about different mathematical constant and get the values for them to solve mathematical problems. Also, download BYJUS-The Learning App to get learning videos and other learning materials.

Unlock This Answer Now

Start your 48-hour free trial to unlock this answer and thousands more. Enjoy eNotes ad-free and cancel anytime.

Already a member? Log in here.

The letters R, Q, N, and Z refers to a set of numbers such that:

R = real numbers includes all real number

Q= rational numbers

N = Natural numbers

z = integers

Recommended Reading: What Are Dyes In Chemistry

What Does <> Mean In Math

means not equal. For example, 2 + 2 5 2. In computer applications the symbols <> mean not equal. means approximately equal to, or almost equal to. The two sides of a relationship indicated by this symbol will not be accurate enough to manipulate mathematically.

History Of Eulers Number

The number e was discovered in the 1720s by Leonard Euler as the solution to a problem set by Jacob Bernoulli. He studied it extensively and proved that it was irrational. He was also the first to use the letter e to refer to it, though it is probably coincidental that that was his own last initial.

The equation most commonly used to define it was described by Jacob Bernoulli in 1683:The equation expresses compounding interest as the number of times compounding approaches infinity. With the binomial theorem, he proved this limit we would later call e.

We can actually follow the history of e even further back than Bernoulli. It turns out that e is the base for natural logarithms, and since these were studied extensively by John Napier one hundred years before Eulerin 1614e is sometimes also called Napiers constant. Napier published a table of natural logarithms, but didnt include in his publication the constant they were calculated from.

You May Like: Algebra Road Trip Project Answer Key

+ Addition Plus Positive

The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.

The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.

See our page on Addition for more.

An Intuitive Guide To Exponential Functions & E

e has always bothered me not the letter, but the mathematical constant. What does it really mean?

Math books and even my beloved Wikipedia describe e using obtuse jargon:

The mathematical constant e is the base of the natural logarithm.

And when you look up the natural logarithm you get:

The natural logarithm, formerly known as the hyperbolic logarithm, is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718281828459.

Nice circular reference there. Its like a dictionary that defines labyrinthine with Byzantine: its correct but not helpful. Whats wrong with everyday words like complicated?

Im not picking on Wikipedia many math explanations are dry and formal in their quest for rigor. But this doesnt help beginners trying to get a handle on a subject .

No more! Today Im sharing my intuitive, high-level insights about what e is and why it rocks. Save your rigorous math book for another time. Heres a quick video overview of the insights:

Recommended Reading: What Is Energy In Quantum Physics

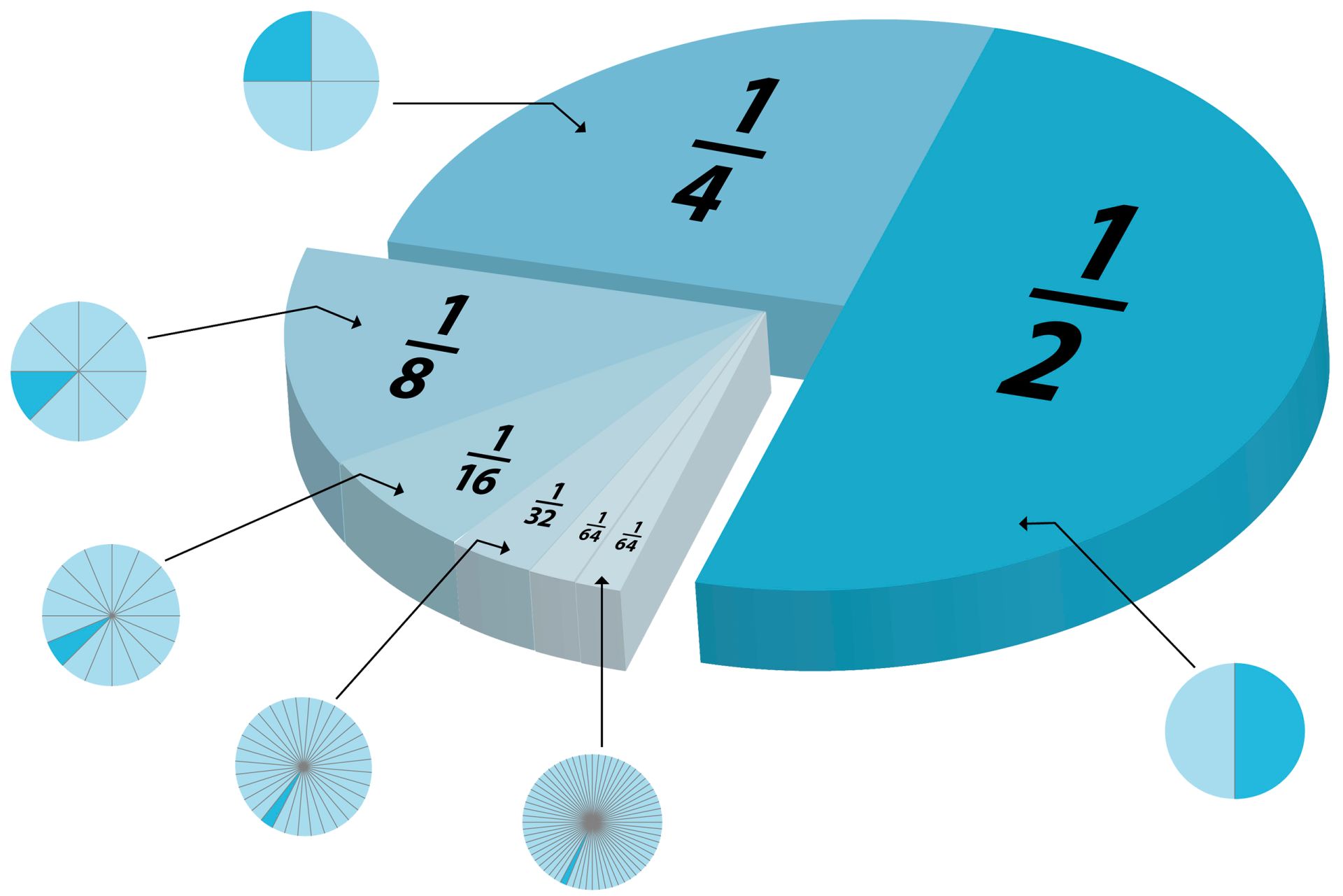
Diving Into Compound Growth

Its time to step it up a notch. Instead of splitting growth into two periods of 50% increase, lets split it into 3 segments of 33% growth. Who says we have to wait for 6 months before we start getting interest? Lets get more granular in our counting.

Charting our growth for 3 compounded periods gives a funny picture:

Think of each color as shoveling money upwards towards the other colors , at 33% per period:

• Month 0: We start with Mr. Blue at \$1.
• Month 4: Mr. Blue has earned 1/3 dollar on himself, and creates Mr. Green, shoveling along 33 cents.
• Month 8: Mr. Blue earns another 33 cents and gives it to Mr. Green, bringing Mr. Green up to 66 cents. Mr. Green has actually earned 33% on his previous value, creating 11 cents . This 11 cents becomes Mr. Red.
• Month 12: Things get a bit crazy. Mr. Blue earns another 33 cents and shovels it to Mr. Green, bringing Mr. Green to a full dollar. Mr. Green earns 33% return on his Month 8 value , earning 22 cents. This 22 cents gets added to Mr. Red, who now totals 33 cents. And Mr. Red, who started at 11 cents, has earned 4 cents on his own, creating Mr. Purple.

Phew! The final value after 12 months is: 1 + 1 + .33 + .04 or about 2.37.

Take some time to really understand whats happening with this growth:

Make sense? Its tough at first I even confused myself a bit while putting the charts together. But see that each dollar creates little helpers, who in turn create helpers, and so on.

Other Differences Between British And American English

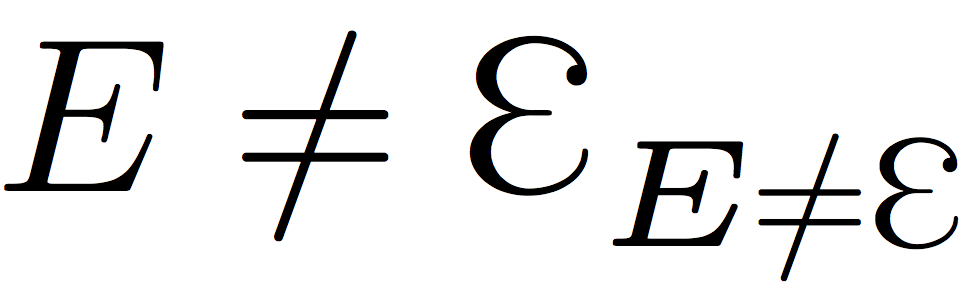
In some cases, British and American English use different words for the same concept. For example, American English speakers use the words truck, shopping cart, and sweater;;British English speakers say lorry, trolley, and jumper to mean the same things.

In other cases, the differences between British and American English words are much more subtle. For instance, American English uses the term racecar, while British English uses the word racing car.

In still other cases, British and American English words differ by just one letter, as in the case of math and maths. British English includes U;in the spelling of French-derived words, such as colour or favourite, which American English omits.

This also happens with the words sport and sports. In American English, youd say, I enjoy playing sports, and I also like watching sports. In British English, this sentence would be I enjoy playing sport, and I also like watching sport. This time, its American English that likes the s!

Don’t Miss: Pre Algebra Order Of Operations Help

How To Remember The Number E

To remember the first ten places of the number e memorizes the saying below. If you count the letters of each of the words, you will get the first ten decimals of the number e. Let’s take a look at some learning fun in this fun math quote to learn complex numbers like the number e.

Remembering the first 9-12 digits with a pattern

You can break the number up to remember the first 9 decimals.

• 7
• 1828

This is easy to remember as the 2.7 is simple and 1828 repeats twice.

Add to these 9 digits and move up to 12 digits easily by remembering the angles of an Isosceles Right Triangle.

• 45

This gives you = 2.71828182845

Raising A Number To A Complex Power

Asked by Wei-Nung Teng, student, Stella Matutina Girl’s High School on June 17, 1997

How do you define a^?a, b, c are real numbers.

example: 5^=?

Thanks

The ordinary definition of exponentiation of real numbers only makes sense when x is rational. To extend the definitionto irrational and then to complex values of x, you need to rewritethe definition in a way that makes sense even when r is complex.

One way to do this is to use the fact that e^x can be expressed asthe infinite sum

It makes perfectly good sense to add and multiply complex numbers, andthe theory about infinite sums can also be extended to complex numbers,so this formula can be used as a definition of what e^x means whenx is complex.

If x is a “purely imaginary” number, that is, if x=ci where c isreal, the sum is very easy to evaluate, using the fact that i^2=-1,i^3=-i, i^4=1, i^5=i, etc. When you do this and split the sum intoits real and imaginary parts, you find that the real part is the sameas the infinite sum expression for cos c, and the imaginary part isthe same as the infinite sum expression for sin c. This gives riseto de Moivre’s formula:

e^ = + i

exxx

Now we know what e raised to an imaginary power is. One can also show thatthe definition of e^x for complex numbers x still satisfies the usualproperties of exponents, so we can find e to the power of any complex numberb + ic as follows:

e^ = ) = + i)

aaa eNavigation Panel:

Don’t Miss: What Does I Stand For In Physics

From Napier Tables To Bernoullis Compounding Interest

In math there are a few, select, magical constants that transverse all branches. These constants, steadily discovered throughout our collective history, provide the numerical infrastructure to our everyday lives; like chemical elements in the periodic table, special constants in math are foundational. To name a few, we have zero , circular-darling pi , square-root of negative one & of course, the exponential king, Eulers constant e .

The focus of this piece, as accurately articulated by the title, is a deep dive into Eulers number, also known as Napiers number or more commonly, simply e. For the uninitiated, the number e is at the very crux of exponential relationships, specifically pertinent to anything with constant growth.

Just like every number can be considered a scaled version of 1 & every circle can be considered a scaled version of the unit circle , every rate of growth can be considered a scaled version of e . E is the base rate of growth shared by all continually growing processes; it shows up whenever systems grow exponentially & continuously: population, radioactive decay, interest calculations, etc E represents the idea that all continually growing systems are scaled versions of a common rate.

Below, were going to visit the three individuals that contributed to its discovery: John Napier, Jacob Bernoulli & Leonard Euler.

What Is An Irrational Number

An irrational number is a number which can not be made into a fraction and whose decimals go on infinitely.

Rational numbers can be written as a fraction as you can see 1.5 can be written as 3/2 and 7 can be written as 7/1. These are rational numbers which can be converted into a fraction and whose decimals do not continue. Thus as the name suggests rational numbers are opposite to irrational numbers. Rational numbers also have a decimal development which is called periodic.

For example,

The digits after the decimal point are a logical and recurring sequence of decimals.

Don’t Miss: What Is Three Dimensional Geometry

Where Does Euler’s Number E Come From

The number represented by e was discovered by mathematician Leonard Euler as a solution to a problem posed by another mathematician, Jacob Bernoulli, 50 years earlier. Bernoulli’s problem was a financial one.

Suppose you put $1,000 in a bank that pays 100% annual compound interest and leave it there for a year. You’ll have $2,000. Now suppose the interest rate is half that, but the bank pays it twice a year. At the end of a year, you’d have $2,250. Now suppose the bank paid only 8.33%, which is 1/12 of 100%, but paid it 12 times a year. At the end of the year, you’d have $2,613. The general equation for this progression is:

where r is 1 and n is the payment period.

It turns out that, as n approaches infinity, the result gets closer and closer to e, which is 2.7182818284 to 10 decimal places. This is how Euler discovered it. The maximum return you could get on an investment of $1,000 in one year would be $2,718.