What Is Three Dimensional Geometry

Surface Area And Volume Of 3d Shapes

The two distinct measures used for defining the 3D shapes are:

• Surface Area
• Volume

Surface Area;is defined as the total area of the surface of the three-dimensional object.; It is denoted as SA. The surface area is measured in terms of square units. The three different classifications of surface area are defined below. They are:

• Curved Surface Area is the area of all the curved regions
• Lateral Surface Area is the area of all the curved regions and all the flat surfaces excluding base areas
• Total Surface Area is the area of all the surfaces including the base of a 3D object

Volume;is defined as the total space occupied by the three-dimensional shape or solid object. The volume is denoted as V. It is measured in terms of cubic units.

To Know About Nets Of Solid Shapes, Watch The Below Video:

Cell Lines Cell Culture And Drug Treatments

Mouse ESCs were routinely cultured as described in Mulas et al. on 0.1% gelatin in PBS in N2B27 medium supplemented with 2i+LIF plus penicillin and streptomycin, at a controlled density in Falcon flasks and passaged every other day using Accutase . They were kept in 37°C incubators with 7% CO2. Cells were regularly tested for mycoplasma.

In this study, the cells used were embryonic day 14 wild-type cells and E14 cells stably expressing H2BRFP . The E14 cells stably expressing H2BRFP were tested for contribution to chimeras, to verify that they were indeed pluripotent, by the Francis Crick Institute mouse facility. Cells were injected into C57BL/6 blastocysts and gave rise to a viable mouse with good contribution of the H2BRFP cells as assessed by the color of the mouse , and via dissection under a fluorescent lamp, which confirmed that the H2BRFP cells contributed to tissues. All animal experiments were performed according to approved guidelines.

The culture medium was made in house, using a 1:1 DMEM/F-12 mixture , Neurobasal medium , 2.2mM L-glutamine, in-house N2 , B27 , 3µM Chiron , 1µM PD 0325901 , LIF , 50mM -mercaptoethanol, 12.5ngml1 insulin zinc . The 200× in-house N2 stock was made using 0.791mgml1 apotransferrin , 1.688mgml1 putrescine , 3µM sodium selenite , 2.08µg;ml1 progesterone and 8.8% bovine serum albumin .

Exit from naïve pluripotency was triggered by removing Chiron, PD 0325901 and LIF.

Size Asymmetries At Division Are Not The Result Of Cortical Contractions

We then explored the mechanisms underlying asymmetric division in ESCs. We observed that cells at the colony periphery displayed significant shape instabilities characterized by strong contractions and blebbing . Previously, myosin-driven contractions at the cell poles during cytokinesis have been shown to lead to asymmetric division in neuroblasts . We thus hypothesized that polar surface contractions and instabilities could be responsible for division asymmetries in ESCs. To assess this hypothesis, we first quantified the occurrence of polar shape instabilities in ESCs dividing at different locations in the 3D colonies. Visual assessment of 3D stacks suggested that 57% of dividing cells showed unstable shapes during cytokinesis . To assess shape instabilities in a more unbiased manner, we further analyzed cell curvature dynamics in 2D, focusing on the midplane of each prospective daughter cell . This analysis was consistent with our visual assessment of 3D stacks, with the cells visually classified as unstable displaying significantly more variable contours . Cells dividing radially displayed more shape instabilities , and cells displaying significant shape instabilities also displayed higher division asymmetries .

Also Check: What Are Dyes In Chemistry

Tips That Will Help You In Preparing Three Dimension Geometry In The Best Possible Way:

• As soon as you are done with the concepts and numerical you must do the previous years questions. With the previous year questions, you would totally understand where you are lacking and you will be able to improve accordingly.

• Take online mock test regularly in a time-bound manner to increase your speed and accuracy. This activity will particularly help you in JEE Mains.

• Know your strength and weakness and try to improve both.

• While practicing if you feel that any question which appears to be important then make a note of that. Later while revising this chapter, you must solve that question again, this will help you to brush up your concepts.

• You must create small formula notebook/flashcards for this chapter and then revise them on a weekly basis to keep them in your mind always.

Why Is Three Dimensional Geometry Important

In most board exams, three-dimensional geometry plays a crucial role. Since it is highly scoring, most students who find the remaining questions challenging to answer can find their solace in this one. Also, three-dimensional geometry is relatively simple to understand. That is why those who pay attention from the start have a broad scope of topping their math papers shortly.

Recommended Reading: What Does Abiotic Mean In Biology

Three Dimensional Geometry: Formulas

In 3 dimensional geometry, a coordinate system relates to the process of recognising the position or location of a point in the coordinate plane. Everything in the present environment is in a three-dimensional shape. Even a horizontal piece of paper has some thickness if we look sideways. So, lets start by understanding lines, planes, and angles.

Escs Growing At The Periphery Of 3d Colonies Display Strong Size Asymmetries At Cell Division

ESCs display strong size asymmetries at cell division. Representative time-lapse images of colonies of naïve ESCs expressing H2BRFP and labeled with CellMask Deep Red with a cell dividing inside the colony and a cell dividing at the periphery of the colony . A single Z-plane is shown. Scale bars: 10µm. Cell boundaries are highlighted with yellow dotted line. Images on the right illustrate segmented 3D cell shapes. Dot plot representing the size asymmetry ratio measured in 3D between daughter cells for single ESCs , ESCs dividing inside of a colony and ESCs dividing at the periphery of a colony with the mitotic spindle oriented parallel or perpendicular to the colony border. The mean±s.d. are shown. Datapoints corresponding to isolated ESCs were replotted from Chaigne et al. , data for cells dividing in colonies were obtained by re-analyzing videos acquired for Chaigne et al. . Example plots showing the evolution of the volumes of daughter cells after cell division at the periphery of the colony, in cases where the outside cell is the bigger one or the smaller one . 0 is the time of cytokinesis. The time when the size asymmetry reported in D is measured is highlighted with a dashed line. Dot plot showing the size asymmetry ratio between daughter cells for cells dividing at the periphery of the colony, with the outside-positioned daughter cell being the bigger one or the smaller one . The mean±s.d. are shown . P-values were calculated with a MannWhitney test.

Recommended Reading: Pre Algebra Order Of Operations Help

Direction Cosines Of A Line

The cosines of the angles made by a directed line segment with the coordinate axes are called the direction cosines of that line.

As shown in the figure above, if , , and are the angles made by the line segment with the coordinate axes then these angles are said as direction angles; and the cosines of these directional angles are the direction cosines of the line.;

Also, cos , cos , and cos are called the direction cosines and are denoted by l, m, and n respectively.

l = cos ,;

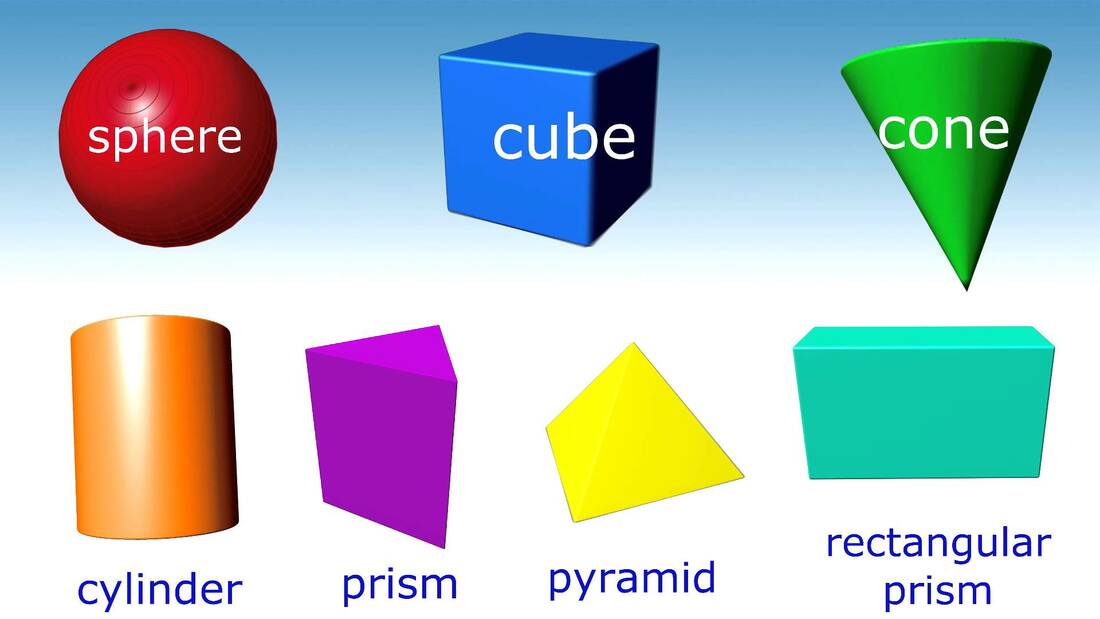
Faces Edges And Vertices Of Three Dimensional Shapes

Three-dimensional shapes have many attributes, such as vertices, faces, and edges. The flat surfaces of the 3D shapes are called faces. The line segment where two faces meet is called an edge. A vertex is a point where three edges meet.

Also, read: Vertices, Edges and Faces

Faces, Edges and Vertices

The list of 3d shapes are given below:

CubeCuboidCylinderConeSpherePrismPyramid

Here, we are going to discuss the list of different three-dimensional shapes with their properties and the formulas of different 3D shapes.

Xem thêm: Integ R Integral Package Computing Integrals With R

Read Also: Eoc Fsa Warm Ups Algebra 1 Answers

Coordinates Of A Point In Space

Consider a point P in space. The position of the point P is given by the coordinates where x, y, z denote the perpendicular distance from YZ-plane, ZX-plane, and XY-plane respectively. If the vectors i, j, k; are assumed to be the unit vectors along OX, OY, OZ respectively, then the position vector of point P is xi + yj + zk or simply .

If O is the origin and P is any point with coordinates from the origin then the distance vector OP by the distance formula is given by OP = x2 + y2 + z2.

Rectangular Coordinate System In Space

The coordinate system defines the position of a vector. In the rectangular coordinate in space, we refer to the three-dimensional space. To demonstrate the position of a vector mark a point as the origin, represented by the point O. The distance of any vector is now measured from this standard point.

Let O be any point in space called origin and XOX, YOY and ZOZ be three lines perpendicular to each other and these three lines denote the coordinate; X, Y, and Z-axis. The planes XY, YZ, and ZX are called the coordinate planes in space.;;;

Also Check: How To Find Biological Grandparents Uk

Variability In The Three

A large database of 3D fault surface geometry from different geologic settings.

Comparison of fault surface geometry based on segmentation characteristics.

Faults typically comprise both bifurcating and unconnected segments.

Fault geometry is controlled by the heterogeneity of the faulted sequence and pre-existing structure.

Best Book For Three Dimensions Geometry :

Maths NCERT Books are one of the most important study material as this book covers all the topics. Start from NCERT book, the example given in NCERT is simple and lucid. Most of the important concepts and theory you will understand by simply solving those given example. And also solve all problems of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the books Vectors & 3D Geometry by Amit M. Agarwal, Cengage Mathematics Vectors & 3D Geometry or RD Sharma. 3D Geometry explained very beautifully in the book Arihant Algebra and there are lots of questions with crystal clear concepts. But again the choice of reference book depends on you, find the book that best suits you the best depending on how well you are clear with the concepts and the difficulty of the questions you require. Rather than referring all the books just stick to one good book but for practicing more problem you can refer to other books.

Also Check: Practice 2 4 Reasoning In Algebra Answer Key

Introduction To Three Dimensional Geometry

Three Dimensional Geometry is the study that deals with the maths of different shapes in a three-dimensional area and this involves three coordinates. The coordinates are x-coordinate, y-coordinate and z-coordinate, respectively. Here, there is a high demand for three parameters to find the specific location of a point.

Although three dimensional geometry is as easy as it can get, some people genuinely have an issue trying to understand it. If you are also one of them, heres an introduction on the same. Make sure you read this to the end so that you can understand the subject without any inconvenience. It will also help you score better grades in your exams next time. So, why not make the most of it?

How To Make 3d Shapes For Maths Project

If you know what three-dimensional shapes are, it would be easy for you to build a 3d shape project for a house or a building. This would be easy for the students to make as they can measure the rooms easily. Rest all they need is cardboard, glue, scissors and art supplies to make it look exactly like a mini house or building.

From Chemical Topology To Three

Editors:Balaban, Alexandru T.

• ebooks can be used on all reading devices
• Immediate eBook download after purchase

Hardcover 207,99

• Free shipping for individuals worldwide
• Institutional customers should get in touch with their account manager
• Usually ready to be dispatched within 3 to 5 business days, if in stock
• The final prices may differ from the prices shown due to specifics of VAT rules

Softcover 166,39

• Free shipping for individuals worldwide
• Institutional customers should get in touch with their account manager
• Usually ready to be dispatched within 3 to 5 business days, if in stock
• The final prices may differ from the prices shown due to specifics of VAT rules

• From Chemical Graphs to 3D Molecular Modeling

  Pages 1-24

• Descriptors of Molecular Shape in 3D

  Pages 25-42

• Use of Graph-Theoretic and Geometrical Molecular Descriptors in Structure-Activity Relationships

  Pages 73-116

• Recognition of Membrane Protein Structure from Amino Acid Sequence

  Pages 117-158

• On Characterization of 3D Molecular Structure

  Pages 159-236

• Chemical Graph Theory of Fullerenes

  Pages 237-262

• Recent Work on Toroidal and Other Exotic Fullerene Structures

  Pages 263-296

• Applications of Topology and Graph Theory in Understanding Inorganic Molecules

  Pages 343-414

Size Asymmetries At Division Correlate With Asymmetrically Distributed E

Since the geometry of the colony was affected when cells were plated on E-cadherin, we sought to verify whether colony spreading could by itself lead to reduced division asymmetries. To do so, we used laminin-coated substrates where ESC colonies adopt spread morphologies similar to cells on E-cadherin . We found that, on laminin, ESCs dividing at colony peripheries displayed asymmetries comparable to those for cells dividing at the periphery of 3D colonies, and higher than in similarly positioned cells dividing on E-cadherin . This suggests that higher cell division symmetry in ESCs plated on E-cadherin is not simply due to the spreading of the colonies. We verified that cells plated on laminin displayed a similar heterogeneity in E-cadherin intensity between inner and outer junctions to cells plated on gelatin .

Coordinate Of A Point In Space

In three-dimensional geometry, the coordinates of a point P, is always written in the form of P, where x, y and z are the distances of the point, from the YZ, ZX and XY-planes.

• The coordinates of any point at the origin is
• The coordinates of any point on the x-axis is in the form of
• The coordinates of any point on the y-axis is in the form of
• The coordinates of any point on the z-axis is in the form of
• The coordinates of any point on the XY-plane is in the form
• The coordinates of any point on the YZ-plane is in the form
• The coordinates of any point on the ZX-plane is in the form

Sign of Coordinates in Different Octants:

The sign of the coordinates of a point determines the octant in which the point lies.

Introduction To Three Dimensional Geometry For Class 11 Notes

Introduction to Three Dimensional Geometry For Class 11 Notes are available for students at BYJUS. These notes will help students to have a quick look at the Chapter 12 Introduction to Three Dimensional Geometry for exams. These notes are provided with reference to NCERT textbooks and the CBSE syllabus .

In Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry Notes, we have given all the important concepts related to 3D geometry explained in the chapter. The topics here include:

• Coordinate axes
• Coordinate of point in space
• Distance between two points

Also check: Equation Of A Line In Three Dimensions

Coordinate System In 3d Geometry

In 3 dimensional geometry, a coordinate system refers to the process of identifying the position or location of a point in the coordinate plane. To understand more about coordinate planes and system, refer to the coordinate geometry lesson which covers all the basic concepts, theorems, and formulas related to coordinate or analytic geometry.

Dot Product Angle And Length

A vector can be pictured as an arrow. The vector’s magnitude is its length, and its direction is the direction the arrow points. A vector in 3 can be represented by an ordered triple of real numbers. These numbers are called the components of the vector.

The dot product of two vectors A = and B = is defined as:

A

\cdot \mathbf =\|\mathbf \|\,\|\mathbf \|\cos \theta ,}

where is the angle between A and B.

The cross product or vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ×. The cross product a × b of the vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, and engineering.

The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.

One can in n dimensions take the product of n 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.

t . \mathbf \cdot \,d\mathbf =\int _^\mathbf )\cdot \mathbf ‘\,dt.}

where · is the dot product and r: C is a bijectiveparametrization of the curve C such that r and r give the endpoints of C.

d t f\,\mathrm S=\iint _f)\left\| \over \partial s}\times \over \partial t}\right\|\mathrm s\,\mathrm t}

Angle Between Two Lines

The angle between two lines whose direction cosines are l1, m1, n1 and l2, m2, n2 is given by:;cos = l1 l2 + m1 m2 + n1 n2

The angle within two lines whose direction ratios are proportional to a1, b1, c1 and a2, b2, c2 respectively is furnished by: \

Points to Recognize

• The two lines are said to be perpendicular if and only if l1 l2 + m1 m2 + n1 n2 = 0
• The same two lines are said to be parallel if and only if: \
• The two lines are said to be perpendicular if and only if a1 a2 + b1 b2 + c1 c2 = 0
• The same two lines are said to be parallel if and only if: \

Moving towards the next important concept, i.e planes. We will be covering the equation of a plane in a different form, distance measurement from point and line as well.