What Is Kinetic Energy In Physics

Can A Collision Conserve Kinetic Energy Without Conserving Momentum

GCSE Science Revision Physics “Kinetic Energy”

In general, it is not possible for a collision to conserve kinetic energy without conserving momentum as the law of momentum conservation prohibits this. This can, however, occur the other way around, meaning that a collision can conserve momentum without conserving kinetic energy.

The collisions in which momentum is conserved but kinetic energy is not are again called inelastic collisions. However, there does not exist a collision type in which momentum would not be conserved.

Examples Of Kinetic Energy

Lets take a look at a 5 best examples of kinetic energy to make it clearer:

Person on a motorcycle: we see that they experience an increase in both potential energy and in kinetic energy . A heavier person will be able to acquire more kinetic energy if the motorcycle allows him to move faster.

A phone that falls to the ground : This type of example is very important in understanding kinetic energy. Energy builds up in your body as it descends, and is completely released when it breaks free from hitting the ground. This is the first hit that starts generating kinetic energy. The rest of the kinetic energy is acquired by the gravity of the Earth.

Ball hitting : A case similar to what happens with a phone. The ball at rest finds equilibrium, and kinetic energy begins to be released from the moment we hit it. The heavier and larger the ball, the more effort it will take to stop or move it.

When we throw a stone from a slope: As the rock descends the slope, its kinetic energy increases. Energy will depend on the mass and the rate at which it falls. This, in turn, will depend on the bias.

Roller coaster: Amusement parks are the key to explaining kinetic energy. On a roller coaster, the car gains kinetic energy when it falls and increases its speed.

I hope that with these five examples of kinetic energy, the concept and its use will become clearer to you.

Kinetic Energy Examples In Everyday Life

If you think you cant relate to kinetic energy examples in everyday life. Well, here is your chance to think again!

A bullet fired from the gun has kinetic energy.
The kinetic energy of a fast stream of water is used to run water mills.
Any object that is freely falling due to gravity has kinetic energy.
The kinetic energy of air is used to run the windmills.
The earth revolving around the sun has kinetic energy.
An Electron revolving around the nucleus has kinetic energy, etc.

Check out:Top 6 Sources of Mechanical Energy You Should Know

Thats it for this post. If you like this article, You can also find us on Mix, and Hey man, If you have come this far, do give us feedback in the comment section. It would make my day. Cheers!!!

Also Check: Segment Addition Postulate And Midpoint Worksheet Answer Key

Examples Of Energy Of 1 Joule

One joule in everyday life and in science corresponds to approximately:

The kinetic energy of an object with mass 1 kg moving at 2 1.4 m/s.
The kinetic energy of a 50 kg object moving very slowly approximately 0.72 km/h.
The energy required to lift a medium-size apple 1 meter vertically from the surface of the Earth.
The heat required to raise the temperature of 1 g of water by 0.24 °C.
The heat required to evaporate of 0.00044 g of liquid water at 100°C.
The amount of electricity required to light a 1 watt LED for 1 s.
Is released by approximately 3.11010 fissions in a nuclear reactor.

What Is Kinetic Energy And Potential Energy Formula

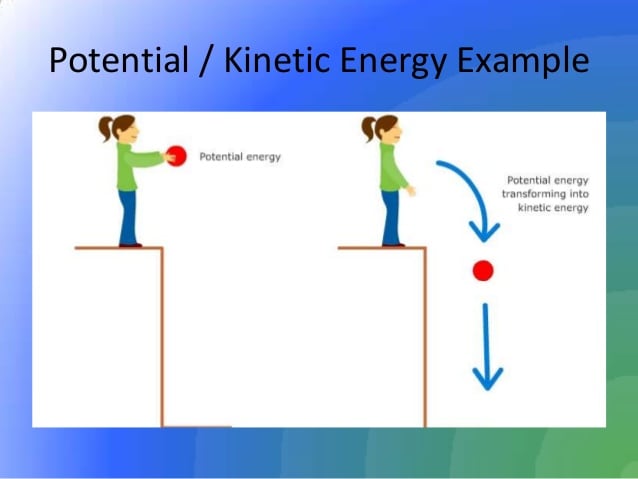
Potential energy and kinetic energy are both measured in joules , named after the English mathematician, James Prescott Joule. But they have different formulas with respect to their different attributes.

Potential energy depends on the force acting on the two objects, so its formula is:

Potential Energy = mgh

m is the mass measured in kilograms
g is the acceleration due to gravity
h is the height in meters

Kinetic energy is directly proportional to an objects mass and the square of its velocity. Putting it in a formula we get:

Kinetic Energy = 1/2 m v²

m is the mass measured in kilograms
v is the velocity of meters per second

Also Check: What Does Abiotic Mean In Biology

Odd Vs Even Powers Of Velocity

There is also another, arguably more fundamental way to see why momentum has a linear velocity-dependence and kinetic energy has a quadratic one and this comes from special relativity.

I actually have a whole section later in the article discussing both momentum and kinetic energy in special relativity , but for the short summary, momentum and kinetic energy in special relativity are given by the following equations:

This -factor is called the Lorentz factor and it is defined as follows:

These formulas are actually more fundamental definitions than the typical ones youre probably used to from ordinary mechanics.

The interesting thing is that this Lorentz factor can be expanded in something called a Taylor series as follows:

If we now insert this to the formulas for the momentum and kinetic energy, we then get:

From this, we can see an interesting fact momentum contains terms with v, v3, v5 and so on, while kinetic energy has terms with v2, v4, v6 etc.

In other words, a more accurate statement of momentum depends linearly on velocity and kinetic energy quadratically would actually be that momentum depends on odd powers of velocity, while kinetic energy depends on even powers of velocity.

Now, the significance of this is that kinetic energy will always be positive, while momentum can be either positive or negative. This is because any even power of velocity has to be positive.

Momentum Conservation Vs Conservation Of Kinetic Energy

An important distinction between momentum and kinetic energy is that, in certain situations, their conservation properties may be different.

Momentum is always a conserved quantity, while kinetic energy is not. Kinetic energy may be converted to other forms of energy, but total momentum in a system always remains the same. Examples of this are collisions in which momentum is conserved, but kinetic energy gets converted into heat and sound.

This really comes down to how we define these two quantities. Kinetic energy is only one form of energy and the conservation of energy only applies to total energy.

Now, the total energy in any system will always be conserved , but there is no conservation law specifically for kinetic energy. Therefore, it can always get converted to other forms of energy.

In contrast, there is no such thing as momentum being converted to other forms of momentum. Therefore, momentum is always conserved in a given system .

This is, however, a little more technical than it may first appear. Momentum actually comes in two forms: linear momentum and angular momentum.

The first one, linear momentum, is the usual form of momentum given by the formula p=mv. Angular momentum, on the other hand, is the momentum associated with rotating or spinning motion.

Also Check: What Is The Molecular Geometry Of Ccl4

Momentum Vs Kinetic Energy In Quantum Mechanics

In quantum mechanics, the relation between kinetic energy and momentum is defined as:

This is essentially the same as in classical mechanics, but the difference is that kinetic energy and momentum are operators in quantum mechanics, not actual physical quantities by themselves. These are represented by putting a hat over them.

But what are these operators used for? Essentially, in quantum mechanics there is something called the wave function, which describes any quantum system. These operators can then act on the wave function to obtain a physical quantity.

In the case of kinetic energy, the kinetic energy operator can act on a wave function to obtain the physical quantity T :

Or written in terms of the momentum:

Also, the definitions of these operators can be expressed in terms of gradients as follows:

Anyway, the point here is that in quantum mechanics, both momentum and kinetic energy are operators, which can act on a wave function to obtain the actual physical values of these. This means that neither momentum or kinetic energy are real physical quantities unless a wave function is specified.

By the way, if youre interested, here are some of my all-time favorite physics books that I know youll enjoy and learn a lot from:

more advanced physics topicsstep-by-step guideintroduction to general relativity

Does Zero Momentum Mean Zero Kinetic Energy

GCSE Physics – Kinetic Energy #2

For a single object, zero momentum always means zero kinetic energy as well. However, for systems of multiple objects, it is possible to have zero total momentum but non-zero kinetic energy in the case that the momenta of each object is exactly equal but in opposite directions.

In the case of a single object, this is easy to see directly from the formula T=p2/2m. If the momentum of this object is zero, the kinetic energy will be as well.

However, the case with multiple objects is easiest to understand through an example. Lets say we have two objects of the same mass moving in opposite directions with the same velocity . This means that they have equal but opposite momentum:

In this case, the kinetic energy will be the sum of the kinetic energies of each object:

Since p1=-p2 and the masses are the same, this becomes:

We can also insert p1=mv1 so that this becomes:

This is clearly non-zero and we therefore have an example of a case where the total momentum is zero, but kinetic energy is not.

Also Check: Practice And Homework Lesson 1.7 Answers

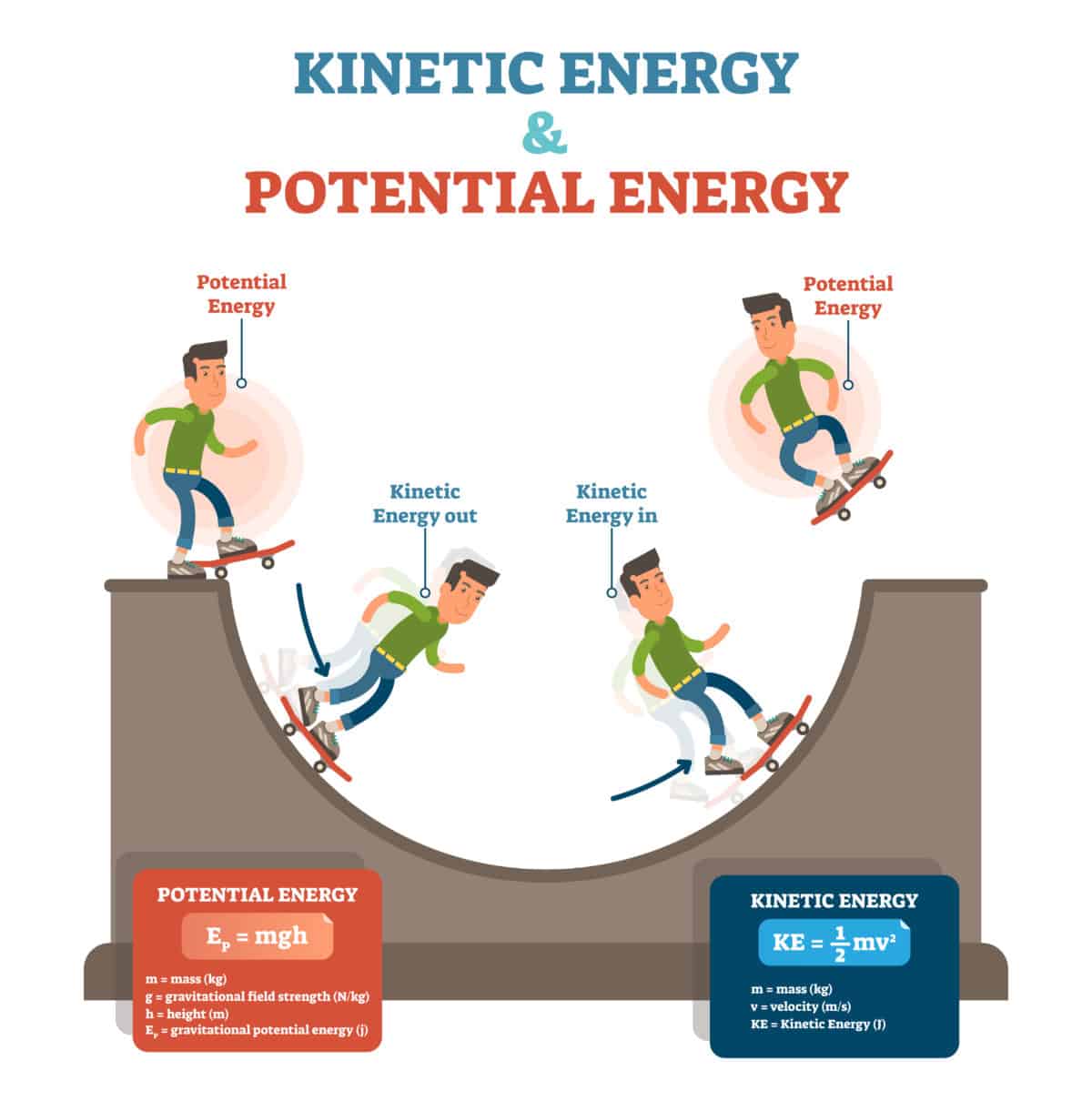
Relationship Between Potential And Kinetic Energy

All objects have potential energy in them. When these objects move, this energy changes into kinetic energy. For example, let us look at a big rock sitting on top of a mountain. When it is just sitting, it has potential energy.

If the rock falls from the mountain slope, it will keep rolling down causing a lot of damage. This potential energy is now changed into kinetic energy. In contrast, if we have a very small rock and it falls down the mountain slope, it will stop after going a few metres and would also not cause any damage or destruction. Thus, heavier objects have more kinetic energy.

Kinetic energy is the reason why any fast moving object cannot stop all of a sudden. So, a fast moving bus cannot immediately stop, or if you are riding a bicycle, you cannot immediately put brakes. Kinetic energy can be passed from one object to another by collision. A good example is a bowling game, where the pins begin moving when the moving ball collides with them.

Looking for more Physics articles and videos? Go to: Physics for Kids.

Is Electrical Energy Potential Or Kinetic

Electrical energy is classified as potential energy before its released and used in the form of power, which is most commonly harnessed and used as electricity. However, once it is converted from its potential state, electrical energy can become one of the subtypes of kinetic energy, including motion or sound, among others.

Kinetic Energy Of Rigid Bodies

In classical mechanics, the kinetic energy of a point object , or a non-rotating rigid body depends on the mass of the body as well as its speed. The kinetic energy is equal to 1/2 the product of the mass and the square of the speed. In formula form:

12.96 kJ }=}\cdot 80\,}\cdot \left^=12,960\,}=12.96\,}}

When a person throws a ball, the person does work on it to give it speed as it leaves the hand. The moving ball can then hit something and push it, doing work on what it hits. The kinetic energy of a moving object is equal to the work required to bring it from rest to that speed, or the work the object can do while being brought to rest: net force × displacement = kinetic energy, i.e.,

is the speed of the center of mass of the body.

The kinetic energy of such systems depends on the choice of reference frame: the reference frame that gives the minimum value of that energy is the center of momentum frame, i.e. the reference frame in which the total momentum of the system is zero. This minimum kinetic energy contributes to the invariant mass of the system as a whole.

Derivation

Without vectors and calculus

The work W done by a force F on an object over a distance s parallel to F equals

) . \cdot d=}d=}dv^=d\left.}

E 2 . }=\int _^\mathbf \cdot d\mathbf =\int _^\mathbf \cdot d=\int _^d\left=}}.}

Momentum Vs Kinetic Energy In Lagrangian Mechanics

Typically in mechanics, things are described by forces and Newtons laws. However, in more advanced classical mechanics, the same concepts are most often described by energies. This is what Lagrangian mechanics is all about.

In Lagrangian mechanics, everything is described by energies and it is always done by defining a Lagrangian for any given system.

Generally, for any system, the Lagrangian is the difference between the kinetic and potential energies of each object in the system:

Now, if youre interested to learn more about this, Id recommend reading my introductory article on Lagrangian m echanics.

Anyway, the point here is that kinetic energy in Lagrangian mechanics is the exact same as it is in ordinary mechanics.

Momentum, on the other hand, has a different definition. Momentum in Lagrangian mechanics is defined as the derivative of the Lagrangian with respect to velocity:

This is actually not quite the correct definition yet, but from this, you can clearly see the similarity to what I explained earlier about momentum as the derivative of kinetic energy.

In Lagrangian mechanics, it is typical to use generalized coordinates . By using these, the definition for momentum is a little different, but the basic idea is the same. You can read more about this as well in my introductory article .

Anyway, in most cases, the above definition is simply just momentum equals the derivative of kinetic energy, however, not always.

The Lagrangian is then :

Don’t Miss: What Is An Example Of Movement In Geography

What Is The Relationship Between Potential And Kinetic Energy

Although these primary forms of energy are very different, they are complementary to one another.

Potential energy always leads to kinetic energy when it is released, and kinetic energy is needed to allow an object to store energy as potential, in one way or another. For example, a rock on the edge of a cliff does not directly need kinetic energy to store the potential energy that will send it down the eroding cliff face. But the act of erosion to get the rock to the edge requires kinetic energy. Therefore, the rock requires it for its potential energy.

Given that these are the two main forms of energy in the world, especially on the human scale, theres a constant push and pull between potential energy and kinetic energy in everyday life.

Kinetic Energy As The Integral Of Momentum

If momentum is the derivative of kinetic energy, does this mean that kinetic energy is then the integral of momentum?

In short, kinetic energy is indeed the integral of momentum with respect to velocity. More accurately, the line integral of momentum with respect to the velocity vector at each point along a path gives the total change in kinetic energy. Physically, this represents the work done along the path.

The change in kinetic energy is mathematically defined as:

Technically, this is actually a line integral, which simply means an integral along a specific path.

Now, the physical meaning of this is that between the end points of the path .

Also, the mathematical proof you can use to verify that this works is extremely easy just plug in p=mv and calculate the integral. You can see this quite easily by simply writing out the dot product and splitting out the integrals component by component:

Read Also: My Hrw Com Algebra 1

Is Momentum Proportional To Kinetic Energy

In short, momentum is proportional to the square root of kinetic energy since momentum is directly proportional to velocity, while kinetic energy is proportional to velocity squared. This means that if kinetic energy becomes four times as big, the momentum will only double.

This can also be seen from the relationship between momentum and kinetic energy if we solve for p:

From this, its easy to see that momentum is proportional to the square root of kinetic energy, while kinetic energy is proportional to the square of momentum:

Different Types Of Potential Energy

Physics – What is Kinetic Energy – Work and Energy – Part 4 English

Electrical potential energy is the energy stored between the plates of a charged capacitor.
Chemical energy, the ability of a substance to work or to produce heat from a change in structure, may be considered as potential energy arising from the reciprocal forces between its molecules and atoms.
Nuclear energy is a form of potential energy as well.

You May Like: Elton John Children Biological

What Is The Potential Energy Of An Electron

Electrons are in motion, so they contain kinetic energy. This is one of the best examples of a nonphysical object carrying kinetic energy.

However, its still possible to discern the potential energy that an electron has stored. To find this potential energy, it requires a complicated formula:

U = -qeV = -keqe2/r

The total energy is the sum of the electrons kinetic energy and its potential energy, which is represented by an even more complicated formula:

KE+PE=-½keqe2/r=/ J = -2.18*10-18 J

Phet: Energy Skate Park

The University of Colorado has graciously allowed us to use the following PhET simulation. Explore this simulation to see how gravitational potential energy and kinetic energy go back and forth but keep mechanical energy the same. Notice how mechanical energy can be lost and turned into thermal energy, but the total amount of energy still stays the same: