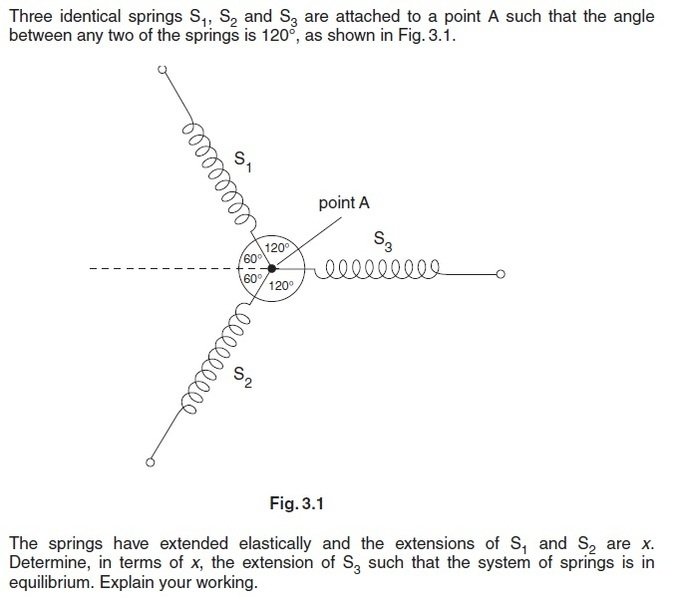
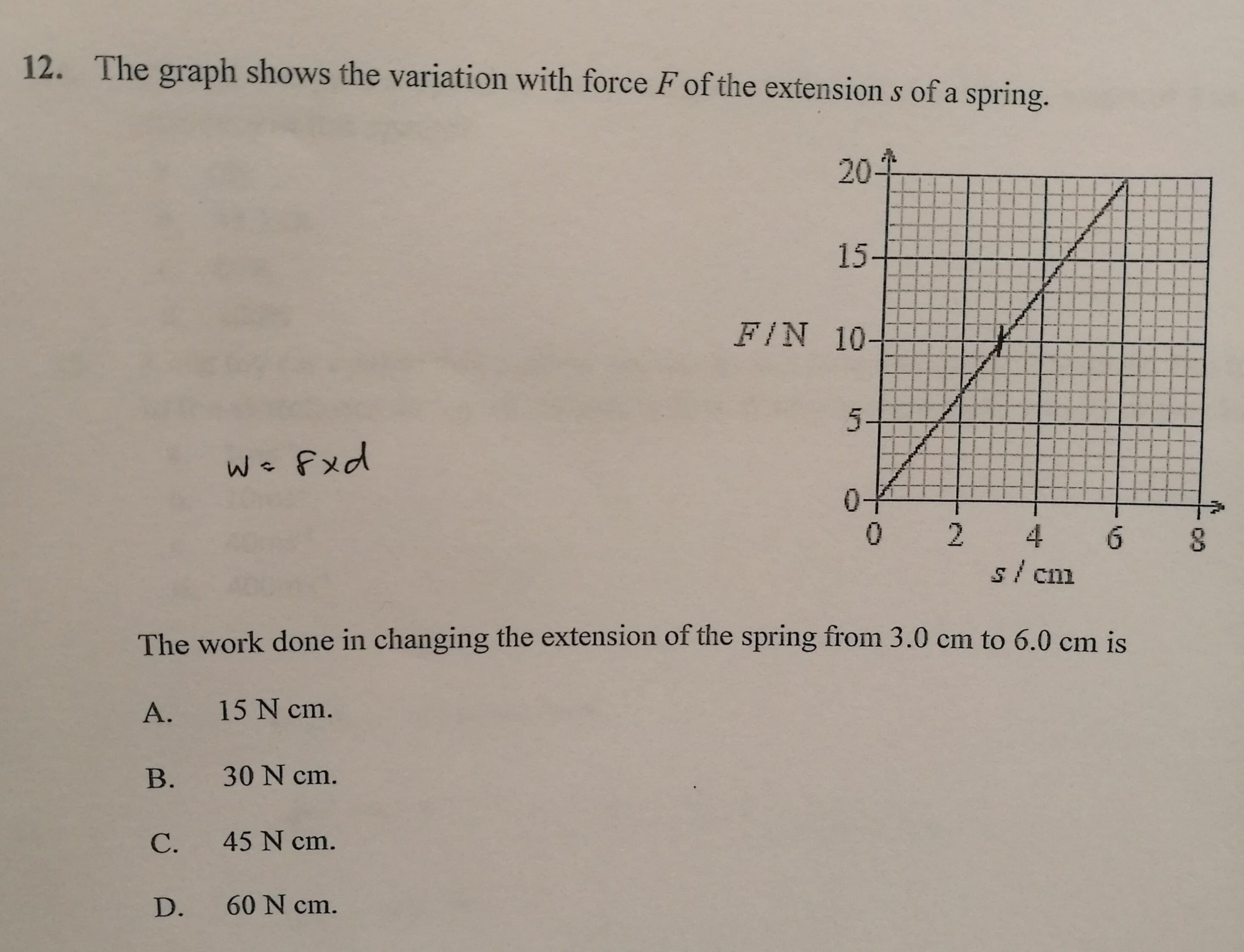
How To Calculate Extension In Physics

How To Calculate Tension In Physics

This article was co-authored by Bess Ruff, MA. Bess Ruff is a Geography PhD student at Florida State University. She received her MA in Environmental Science and Management from the University of California, Santa Barbara in 2016. She has conducted survey work for marine spatial planning projects in the Caribbean and provided research support as a graduate fellow for the Sustainable Fisheries Group.There are 7 references cited in this article, which can be found at the bottom of the page.wikiHow marks an article as reader-approved once it receives enough positive feedback. This article has 15 testimonials from our readers, earning it our reader-approved status. This article has been viewed 1,633,307 times.

In physics, tension is the force exerted by a rope, string, cable, or similar object on one or more objects. Anything pulled, hung, supported, or swung from a rope, string, cable, etc. is subject to the force of tension.XResearch source Like all forces, tension can accelerate objects or cause them to deform. Being able to calculate tension is an important skill not just for physics students but also for engineers and architects, who, to build safe buildings, must know whether the tension on a given rope or cable can withstand the strain caused by the weight of the object before yielding and breaking. See Step 1 to learn how to calculate tension in several physical systems.

Example 2 Parallel Springs

Two springs are attached to a block as shown. Calculate the force required to compress both by 10 cm.

Solution : In this case, the overall spring constant k is just the sum of the individual spring constants:

$$k = k_1 + k_2$$

So $k = 120 \; N/m + 80 \; N/m = 200 \; N/m$.

Now it’s a straightforward calculation of the force using Hooke’s law and the displacement, |x| = 10 cm.

$$F = k|\Delta x| = 200 \; N/m = 2 \; N$$

The force required to compress or extend multiple springs is just the sum of the forces to compress/extend each spring individually. In this arrangement, the springs are said to work in parallel.

Example 1: The Stretch Of A Long Cable

Suspension cables are used to carry gondolas at ski resorts. Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is 3.0 × 106 N.

Figure 4.

Strategy

The force is equal to the maximum tension, or F = 3.0 × 106 N. The cross-sectional area is ;r2 ;= ;2.46 × 10-3 m2. The equation \boldsymbol = \frac\fracL_0} can be used to find the change in length.

Solution

All quantities are known. Thus,

Discussion

This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.

Figure 5.

You May Like: What Is Energy In Quantum Physics

Torque Wrench Extension Example

How to calculate the torque setting on a wrench extension?

Example 3 Springs In Series

A mass is attached to two springs as shown. The spring on the right is compressed 20cm from its natural length. Calculate the force required to move the mass 10 cm to the left, at constant velocity.

Solution : In this situation, the spring on the left needs to be compressed, and because the spring on the right is compressed, it will provide some of the force needed to move the mass. We aren’t accelerating the mass, so we don’t have to exert a net force just to move it.

The force required to compress the spring on the left is

$$F_1 = – = 1.2 \; N$$

The force toward the left produced by the spring on the right is

$$F_2 = – = -0.8 \; N$$

Now the net force required to make the move is the sum of these two forces,

$$F_1 + F_2 = 1.2 \; N – 0.8 \; N = 0.4 \; N$$

You May Like: What Is Said To Be The Origin Of Chemistry

Maximum Spring Extension Equation

Definition: The maximum spring extension of a tension spring is the elastic limit the spring is able to achieve due to the proportion of its physical dimensions.

Our spring calculator, Spring Creator, is able to calculate your tension springs elastic limit using a maximum spring extension equation which has been added into its calculating software. This value on our calculator is known as Maximum Safe Travel Considering Hook Stress . By making the distance traveled of your spring longer than this value, thus exceeding its elastic limit, you will cause the extension spring to take a set.

Get our New Free Spring Creator App for Android and iOS Devices

Maximum Spring Extension

Besides the Maximum Safe Travel Considering Solid Height, there is an additional value called Maximum Safe Travel. The difference between the two is that one of the values considers the stress being applied on the hooks as your spring is extended while the other value is the amount of travel you would be able to achieve out of your spring if you were to remove the hooks.

Assisting Diagrams

The amount stated in Maximum Safe Travel Considering Hook Stress is calculated by considering the tightness of the coil forming the hook as well as the tensile strength of the material selected. These values amongst others are what makes our extension spring calculator automatically calculate the stress one the hook after a certain amount of load.

What Is Hooke’s Law

by Matt Williams, Universe Today

The spring is a marvel of human engineering and creativity. For one, it comes in so many varieties the compression spring, the extension spring, the torsion spring, the coil spring, etc. all of which serve different and specific functions. These functions in turn allow for the creation of many man-made objects, most of which emerged as part of the Scientific Revolution during the late 17th and 18th centuries.

As an elastic object used to store mechanical energy, the applications for them are extensive, making possible such things as an automotive suspension systems, pendulum clocks, hand sheers, wind-up toys, watches, rat traps, digital micromirror devices, and of course, the Slinky.

Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play which together are known as Hooke’s Law.

This can be expressed mathematically as F= -kX, where F is the force applied to the spring ; X is the displacement of the spring, with a negative value demonstrating that the displacement of the spring once it is stretched; and k is the spring constant and details just how stiff it is.

There are also some great resources online, such as this lecture on Hooke’s Law that you can watch on academicearth.org. There is also a great explanation of elasticity on howstuffworks.com.

Also Check: Why Are There Different Branches Of Chemistry

Tensional Stress Of A Uniform Bar

A rod of any elastic material may be viewed as a linear spring. The rod has length L and cross-sectional area A. Its tensile stress is linearly proportional to its fractional extension or strain by the modulus of elasticityE:

2 }=}kx^}

which comes from adding up the energy it takes to incrementally compress the spring. That is, the integral of force over displacement. Since the external force has the same general direction as the displacement, the potential energy of a spring is always non-negative.

This potential Uel can be visualized as a parabola on the Ux-plane such that Uel = 1/2kx2. As the spring is stretched in the positive x-direction, the potential energy increases parabolically . Since the change in potential energy changes at a constant rate:

d . U_ }}}}=k\,.}

Note that the change in the change in U is constant even when the displacement and acceleration are zero.

The Force Produced By Springs

Hooke’s law says that the force produced by a spring is proportional to the displacement of that spring:

F = -kx

where k is called the force constant or spring constant of the spring. Each spring has its own force constant.

The diagram defines all of the important dimensions and terms for a coil spring. For each mass hung on it , a spring has some natural length, at which it is neither compressed or extended . At that point, the upward force produced by the spring is exactly balancing the gravitational force on the mass and spring .

We define the coordinate x so that it is negative when the spring is compressed, zero at the natural length and positive when the spring is extended. The minus sign in F = -kx is there by convention; we think of F as the restoring force. When the spring is compressed, a positive force is required to extend it, and when it is extended, a negative force is required to shorten it, or restore it to its natural length.

If the spring is strong or stiff, k will be large, and k will be small for a weak spring.

Hooke’s law is applicable not only to coil springs like the one shown here, but also to the bending of metal and some other materials, the stretching of wires like guitar strings, the stretching of rubber bands, and the stretching and compressing of chemical bonds.

Also Check: What Is Ap Biology In High School

Calculating Extension A Block Of Mass Being Pulled

A block of mass $m$ and length $l$, kept on a frictionless surface, is being pulled towards right with constant force $F$. How can we calculate the total extension in block? It is given that Young’s modulus of the material is $Y$.

I tried drawing freebody-diagrams but with that, I get net extension as zero!

According to my method, we take elementary slice dx, and make freebody diagram. Balancing forces, we get $$\dfrac = F_$$

Now, we let elementary extension be $dl$, Then:

$$dl = \dfrac}dx\\\Delta l = \int_0^l\dfracdx = 0$$

This seems quite incorrect. What is the correct way to understand and solve this problem?

Answer given was $\Delta l = \dfrac$

You have the right idea to think about slices of thickness $dx$. Let’s remember what happens if the left hand side is fixed. Then each slice experiences a force $F$, and the slice of thickness $dx$ gets an extension of $\dfrac * dx$. Then the total extension is the sum of the extensions of each slice: $\int_0^l \dfrac * dx = \dfrac$.

Now let’s consider the case where the left side is free to move. Then the force in the far left most slice is actually zero, and in general the force at any slice is proportional to the mass to the left of it . So the force in the slice at $x$ is $F\cdot \dfrac$. Therefore the extension of this slice is $\dfrac \dfrac * dx$, and so the total extension is $\int_0^l \dfrac \dfrac* dx = \dfrac.$

Example 2: Calculating Deformation: How Much Does Your Leg Shorten When You Stand On It

Calculate the change in length of the upper leg bone when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 40.0 cm long and 2.00 cm in radius.

Strategy

The force is equal to the weight supported, or

and the cross-sectional area is ;r2; = ;1.257;× 10-3 m2. The equation \boldsymbol = \frac\fracL_0} can be used to find the change in length.

Solution

All quantities except;L are known. Note that the compression value for Youngs modulus for bone must be used here. Thus,

Discussion

This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 3 have larger values of Youngs modulus Y. In other words, they are more rigid.

The equation for change in length is traditionally rearranged and written in the following form:

The ratio of force to area, \boldsymbol},; is defined as stress, and the ratio of the change in length to length,\boldsymbol}},is defined as strain . In other words,

In this form, the equation is analogous to Hookes law, with stress analogous to force and strain analogous to deformation. If we again rearrange this equation to the form

we see that it is the same as Hookes law with a proportionality constant

Don’t Miss: How To Do Elimination In Math

What Is Tension Force

Imagine that you pick up a basketball from the ground. You would feel the ball’s weight in your hands because of the force of gravity acting on the ball’s mass. Now imagine tying a rope around the ball, which you then use to lift the ball again. You would still feel the ball’s weight through the rope. In this situation, the rope is now in tension. What keeps the rope together is called the tension force. Cutting the rope will release the tension force and would put the ball in free fall.

Tension force is an axial force that passes through an object that pulls, like a rope, string, or chain. We can also observe tension force in other materials, like rods and bars, given that they are subjected to external pulling or tensile loads. Materials with high tensile strength make the best rods and bars as they don’t break easily when subjected to tension forces. You can check our stress-strain calculator which discusses about elasticity to learn more about tensile strength.

Tension force is also a great example of Newton’s Third Law of Motion. Newton’s Third Law of Motion states that when a body exerts a force on a second body, the second body exerts an equal force in the opposite direction back onto the original body. Tension force is a reactive force that counteracts an external pulling force. This characteristic of tension force is the reason why it is, in a way, quite similar to normal force, which you can learn more about by visiting our normal force calculator.

Hooke’s Law For Continuous Media

The stresses and strains of the material inside a continuous elastic material are connected by a linear relationship that is mathematically similar to Hooke’s spring law, and is often referred to by that name.

However, the strain state in a solid medium around some point cannot be described by a single vector. The same parcel of material, no matter how small, can be compressed, stretched, and sheared at the same time, along different directions. Likewise, the stresses in that parcel can be at once pushing, pulling, and shearing.

In order to capture this complexity, the relevant state of the medium around a point must be represented by two-second-order tensors, the strain tensor and the stress tensor . The analogue of Hooke’s spring law for continuous media is then

=\sum _^\sum _^c_\varepsilon _}

where i,j = 1,2,3.

All three tensors generally vary from point to point inside the medium, and may vary with time as well. The strain tensor merely specifies the displacement of the medium particles in the neighborhood of the point, while the stress tensor specifies the forces that neighboring parcels of the medium are exerting on each other. Therefore, they are independent of the composition and physical state of the material. The stiffness tensor c, on the other hand, is a property of the material, and often depends on physical state variables such as temperature, pressure, and microstructure.

Recommended Reading: What Does Mole Mean In Chemistry

Finding The Maximum Extension Of A Spring

I have solved that after the body m1 hits m2, the velocity of m2 is going to be *v0. I did this by using the law of conservation of momentum and using the coefficient of restitution . I do not know how to proceed to get the max extension in the spring.

You have found the velocity of body 2 after it is hit by the body 1 absolutely correctly. So let’s consider the second part of the process, lasting from the moment of the hit until the moment of the maximum extension of a spring.Let’s put that at initial time, velocity of the body 2 was: $$v_ = \fracv_0$$Appropriately, velocity of the body 3 was zero: $v_ = 0$.

We need to determine somehow when the maximum spring extension would happen. The extension of the spring would be maximum, at the moment when the distance between the bodies is maximum. If the distance is maximum, then the separation speed is zero, it means that the angular velocity of the two bodies would be equal.

Let’s denote the initial and the final angular velocities of the bodies as follows:

$$\omega_ = \frac} = \fracv_0\tag$$$$\omega_ = 0$$$$\omega_ = \omega_ = \omega_$$

$$x=\fracv_0\sqrt}$$So, the correct answer is B

Newton’s Second Law Of Motion

To calculate the tension that acts in a rope, we first need to understand Newton’s Second Law of Motion. Newton’s Second Law of Motion states that the sum of the forces acting on an object of constant mass is equal to the mass of that object multiplied by its acceleration. We can also express this statement as an equation:

F = m * a

• denotes the summation of forces F;
• m is the mass of the object; and
• a is the acceleration.

For an object suspended by a rope, we can use gravitational acceleration, g, as its acceleration. Gravitational acceleration gives us the value of its weight in terms of force, like in Newtons or pound-force. If the object is moving at a different acceleration, we should use its actual acceleration for the calculation. However, this tension calculator only determines the tension forces in cases of static equilibrium.

This statement means that this tool only considers objects at rest in a given system. In this tension calculator, we also assume that ropes are massless and, therefore, do not contribute anything to the tension forces. We also assume that the masses or objects are in a vacuum and do not experience friction or air resistance towards their surroundings.

Read Also: What Is Mean Median Mode And Range In Math