What Is The Formula For Half
The formula for half-life in chemistry depends on the order of the reaction. For a zero order reaction, the formula is t½ = / 2k. For a first order reaction, t½ = 0.693 / k, and for a second order reaction, t½ = 1 / k . Half-life, or t½, is the time that elapses before the concentration of a reactant is reduced to half its initial value.
If the order of a reaction is unknown, sufficient information to determine it must be deduced in order to calculate its half-life. The rate constant, K, for the chemical process or enough information to determine it must be given. In some reactions, the initial concentration needs to be known.
With a zero order reaction, the substrate concentration does not affect the speed of reaction. Decreasing the substrate concentration of this type of reaction decreases the half-life. The original concentration and rate constant will also affect the half-life. With first order reactions, the length of half-life remains constant even if the substrate concentration changes, and only the reaction rate constant affects it. For second order reactions, a constant decrease in the substrate concentration lengthens the half-life. Original concentration and the rate constant determine the half-life in second-order reactions.
What Is Half Life
Many elements of the periodic table, and specially their isotopes âatoms with the same number of protons as a given element but different number of neutronsâ, have unstable nuclei. Such elements are called radioactive. In a spontaneous process called radioactive decay, unstable nuclei emit subatomic particles like protons, neutrons and electrons, or high amounts of energy in the form of gamma rays. This process can initiate a chain reaction, after which atoms with much more stable nuclei are formed.
Radioactive decay is a random process, which means the time needed for an atom to emit radiation is basically uncertain. Just like when flipping coins, you canât be completely sure about which side they might fall on âeven if you know you have a 50/50 chance. All you can do is throw them in the air over and over again until you get the expected result.
Letâs say we do an experiment where thousands of people flip coins and we count those who get tails as time pases. Even though the probability of that happening in each case is 50%, some people might get tails only after several flips, while others might get them right away.
Radioactive decay follows what we call an exponential behavior. This means, the curve above can be described with an equation like this one:
| N=N0e-t |
Half lifes of some radioactive isotopes
| Radioactive isotope | |
| tellurium-128 | 2.2 x1024 years |
How To Use The Drug Half
In order to use our 1/2 life calculator you’ll need the following data:
The half time of a given drug – this input can be either in minutes, hours, or days. The calculator will set the unit of the result automatically.
If you don’t know the half life of the drug, take a look at our table below.
Dosage – the amount of the drug administered at the very start.
Your results will be shown in a table that consists of at least 5 half-life cycles:
Time – the amount of time that has passed since the first administration of a drug;
Dosage – the amount of drug left in the patient’s body at the given time; and
Concentration – the part of the original concentration still present in the patient’s body.
Recommended Reading: How To Find Mu In Physics
Half Life Formula Derivation
First of all, we start from the exponential decay law which is as follows:
N = N0\
Furthermore, one must set t = \ and N) = ½ N0.
N ) = \ = N0\
Now divide through by N0 and take the logarithm,
½ = \, this leads to In = \
Now solving for \,
\ = \\)
Following the laws of logarithms, one can take the -1 up s an exponent of the logarithm. Finally, this gives
\ = \
What Is The Half

In pharmacology, when we talk about the half life of a drug we usually mean the time it takes a drug’s concentration in the blood plasma to reduce by half.
| The half life of a drug describes the amount of time it will take half of the administered drug to be eliminated. |
Why do we need it?
The half-life of a drug helps us assess the potency and toxicity of a drug over a given amount of time. If we know the elimination time, we can easily evaluate how often the drug should be administered to maximize its effect and minimize its adverse reactions.
The concentration of a drug at a given moment crucial in drugs with narrow tolerance range, e.g., medicines that can prolong the patient’s QT and consequently lead to heart arrhytmias.
The half life of a drug is the complete opposite of its doubling time.
Don’t Miss: Holt Geometry Lesson 4.5 Practice B Answers
Solved Examples On Half Life Formula
Q1. Calculate the half-life of a radioactive substance whose disintegration constant happens to be 0.002 1/years?
Answer:; the quantities available here are, = 0.002 1/yearsConsequently, the half life equation becomes:\ = 0.693/ \ = 0.693/0.002 = 346.5
Hence, the half-life of this particular radioactive substance is 346.5 years.
How To Use Our Half Life Calculator
Calculating half-life using the above calculator is very simple because you just have to input values to get half-life of any element. This calculator not only calculates the half-life, but it can also be used to calculate the other parameters of the half-life equation such as time elapsed, initial and remaining value. You can find the different tabs for calculating each parameter.
To calculate the half-life of an element, go to the half-life tab:
Similarly, you can calculate initial and remaining values as well as the time elapsed by clicking on the respective tabs and entering values in the input boxes. You dont need to put any effort into calculating half life because this calculator does all the complex calculations by only taking values and give the results in a blink of an eye. Moreover, you can use this calculator to solve any type of half-life problems in school or college.
Don’t Miss: Pre Algebra Order Of Operations Help
How Does Radioactivity Works
The atoms of heavier elements do not have an ideal proton to neutron ratio. This makes them unstable. In order to approach the stable ratio, the atoms go through radioactive decay and in the process emit energy or various particles as by-products.
The most common types of materials showing radioactive decay are Uranium, Strontium, Plutonium and Radium. The reason for the instability in these and other radioactive materials is that they have extra neutrons in their atoms. This creates imbalance.
Learn what is the significance of Moles? in radioactivity and how to calculate it using mole fraction formula.
What Is Radioactive Decay
Radioactive decay is a method in which unstable atomic nucleus lose energy by generating radiation such as alpha particles, beta particles with neutrino, or a neutrino in the case of electrons capture, gamma rays or electrons when they are converted internally. Materials containing such unstable nuclei are considered radioactive. Some highly excited short-lived nuclear states can decay through the emission of neutrons or protons
Don’t Miss: What Does Abiotic Mean In Biology
How To Calculate Half Life
Half life of a radioactive substance is calculated by measuring the time it takes for its activity to decrease by half. A practical way to estimate half life is to measure the activity of the substance as a function of time, plot the results, and perform an exponential fit of the resulting curve. Finally, half life can be extracted from the parameters of the derived equation.
The Burden Of Knowledge
The flip side of a half-life is the time it takes to double something. A useful guideline to calculate the time it takes for something to double is to divide 70 by the rate of growth. This formula isnt perfect, but it gives a good indication. Known as the Rule of 70, it applies only to exponential growth when the relative growth rate remains consistent, such as with compound interest.
The higher the rate of growth, the shorter the doubling time. For example, if the population of a city is increasing by 2 percent per year, we divide 70 by 2 to get a doubling time of 35 years. The rule of 70 is a useful heuristic; population growth of 2 percent might seem low, but your perspective might change when you consider that the citys population could double in just 35 years. The Rule of 70 can also be used to calculate the time for an investment to double in value; for example, $100 at 7 percent compound interest will double in just a decade and quadruple in 20 years. The average newborn baby doubles its birth weight in under four months. The average doubling time for a tumor is also four months.
We can see how information changes in the figures for how long it takes for a body of knowledge to double in size. The figures quoted by Arbesman are compelling, including:
Arbesman also gives figures for the time taken for the available knowledge in a particular field to double, including:
- Medicine: 87 years
Also Check: What Is Figure Ground Perception Psychology
Timing Using Radioactive Decay:
The half life equation for calculating the elapsed time from the beginning of the decay process to the current moment, related to the beginning of the decay is calculated by using the half-life formula:;;
$$ T = t_ ln / ln $$
Where,
t1 / 2 = half-life of the particle
N_0 = quantity at the beginning
N_t = quantity t changed over time
This equation is also used by half life calculator to find the time elapsed.
Timing Using Radioactive Decay
The formula for calculating the time elapsed from the beginning of the decay process to the current moment, or a chosen moment in the future, relative to the beginning of the decay is calculated using the formula:
where t is the elapsed time, t1/2 is the half-life of the particle, N0 is the quantity in the beginning, and Nt is the quantity at time t. This is the equation used in our tool as well.
You May Like: How To Find Biological Grandparents Uk
Calculating How Much Radioisotope Has Decayed
If we know:
- how much radioisotope was present in the original sample, No
- how much radioisotope is present in the sample after time t, Nt
we can calculate how much of the radioisotope has undergone nuclear decay :
Nd = No – Nt
For example, the mass of iodine-131 remaining in a sample of iodine-131 after 40 days is 0.0469 g. If the sample originally contained 1.50 g of iodine-131, what mass of iodine-131 has undergone nuclear decay?
No = 1.50 g
Nd = No – Nt = 1.50 – 0.0469 = 1.45 g
You could also express this amount as a percentage.What percentage of the iodine-131 has undergone radioactive decay?
| %Nd |
How To Calculate The Half
Confused by exponential formulas? Try our exponent calculator.
Also Check: What Does Kw Mean In Chemistry
The Discovery Of Half
The discovery of half-lives is credited to Ernest Rutherford, one of the most influential physicists of his time. Rutherford was at the forefront of this major discovery when he worked with physicist Joseph John Thompson on complementary experiments leading to the discovery of electrons. Rutherford recognized the potential of what he was observing and began researching radioactivity. Two years later, he identified the distinction between alpha and beta rays. This led to his discovery of half-lives, when he noticed that samples of radioactive materials took the same amount of time to decay by half. By 1902, Rutherford and his collaborators had a coherent theory of radioactive decay . They demonstrated that radioactive decay enabled one element to turn into another research which would earn Rutherford a Nobel Prize. A year later, he spotted the missing piece in the work of the chemist Paul Villard and named the third type of radiation gamma.
Half-lives are based on probabilistic thinking. If the half-life of an element is seven days, it is most probable that half of the atoms will have decayed in that time. For a large number of atoms, we can expect half-lives to be fairly consistent. Its important to note that radioactive decay is based on the element itself, not the quantity of it. By contrast, in other situations, the half-life may vary depending on the amount of material. For example, the half-life of a chemical someone ingests might depend on the quantity.
Rate Of Radioactive Decay
During natural radioactive decay, not all atoms of an element are instantaneously changed to atoms of another element. The decay process takes time and there is value in being able to express the rate at which a process occurs. A useful concept is half-life ), which is the time required for half of the starting material to change or decay. Half-lives can be calculated from measurements on the change in mass of a nuclide and the time it takes to occur. The only thing we know is that in the time of that substance’s half-life, half of the original nuclei will disintegrate. Although chemical changes were sped up or slowed down by changing factors such as temperature, concentration, etc, these factors have no effect on half-life. Each radioactive isotope will have its own unique half-life that is independent of any of these factors.
The half-lives of many radioactive isotopes have been determined and they have been found to range from extremely long half-lives of 10 billion years to extremely short half-lives of fractions of a second. The table below illustrates half-lives for selected elements. In addition, the final elemental product is listed after the decal process. Knowing how an element decays can allow a person to appropriately shield their body from excess radiation.
| Element | |
|---|---|
| 16 | 740 milliseconds |
Interactive Simulation: Visualizing Half-Life
\ is the number of half-lives.
Example \
Solution
Example \
Solution
Don’t Miss: What Is An Experimental Study In Psychology
Drug Half Life Calculator
Our drug half-life calculator is an easy tool to discover the dosage of a drug that is still present in a patient’s system. The half-life of a drug describes the process of its elimination.
Read on to discover the half-life of a drug and how to calculate the half-life of a medication. We’ll also present plenty of useful examples.
This form of half life is not to be mistaken with the !
How Can I Calculate The Half Life Of An Element
Nuclear half-life expresses the time required for half of a sample to undergo radioactive decay. Exponential decay can be expressed mathematically like this:
#A = A_0 * ^)#
– the amount left after t years; #A_0# – the initial quantity of the substance that will undergo decay; #t_# – the half-life of the decaying quantity.
So, if a problem asks you to calculate an element’s half-life, it must provide information about the initial mass, the quantity left after radioactive decay, and the time it took that sample to reach its post-decay value.
Let’s say you have a radioactive isotope that undergoes radioactive decay. It started from a mass of 67.0 g and it took 98 years for it to reach 0.01 g. Here’s how you would determine its half-life:
Starting from , we know that
#0.01 = 67.0 * ^) -> 0.01/67.0 = 0.000149 = ^)#
#98.0/t_ = log_ = 12.7#
You May Like: Geometry Dash Practice Song Hack
Introduction To Half Life Calculator
Half life is explained as the time required for the decay rate of any substance that might be having an unstable structure by a constant factor 2. Hence, if the initial concentration of a particular sample is known as A then, the decay in this amount after half life will be A/2.
Half life calculator is an online way to calculate half life online. The half life formula calculator is an efficient tool which saves you a lot of time doing manual calculations.
How To Find Half Life
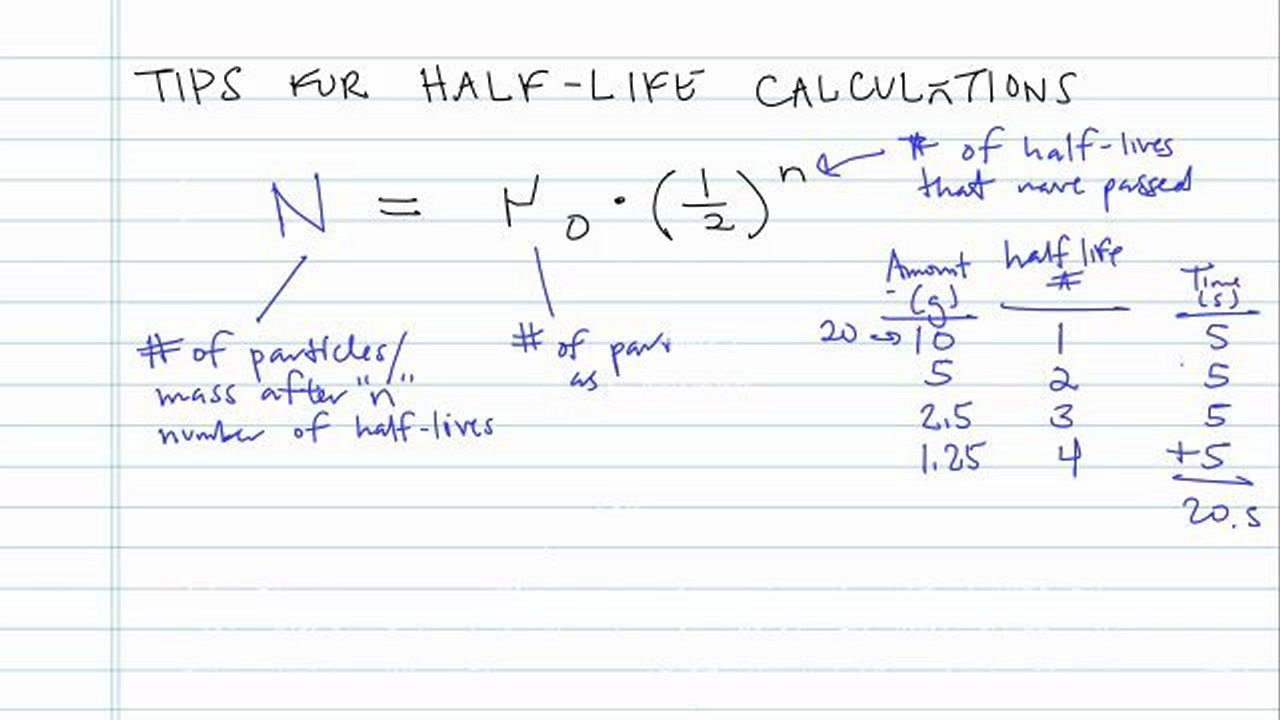
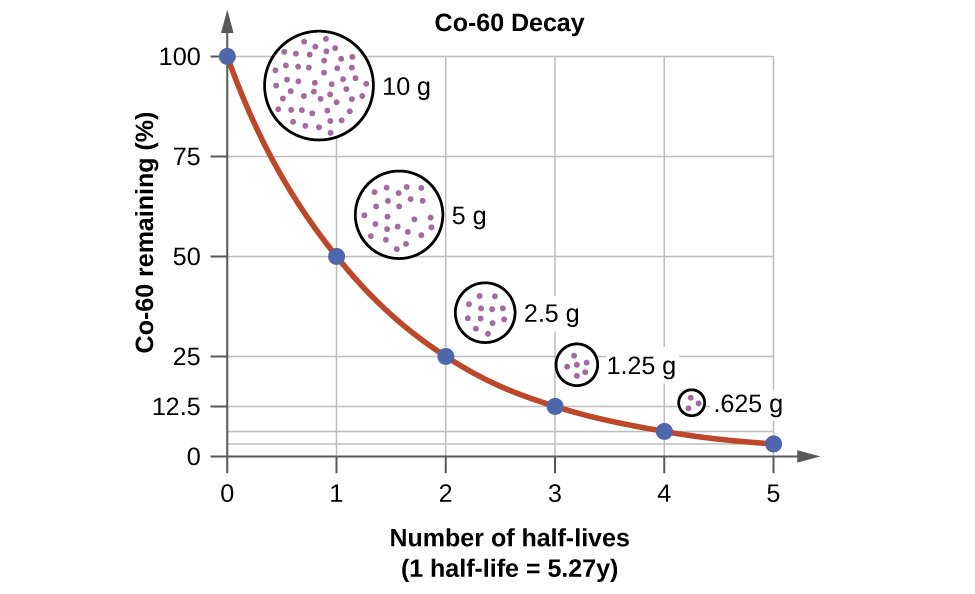
There are 2 ways through which we find half life. The digital method includes the usage of half life equation calculator. And the other is manual way.The time period is associated with half-life, let’s say 7 days means that if you have a considerable number of radioactive atoms with that half-life, then after 7 days, half of them have released their excess energy and decayed into something else.
So if we have 10,000 atoms of Exampelonium-111 with a half-life of 7 days we would only have 5,000 atoms of it. Then 7 days later, we would only have 2,500 atoms, etc. A half life calculator with steps helps you to find the exact time at which a radioactive element need to decay to its half.
You can also learn how to calculate grams to moles? using grams to moles formula.
Also Check: What Is Meant By The Process Of Differentiation In Geography