Theorems Involving Equilateral Triangles
Morley’s theorem states that the three intersection points of adjacent angle trisectors form an equilateral triangle .
In fact, this theorem generalizes: the remaining intersection points determine another four equilateral triangles. Additionally, an extension of this theorem results in a total of 18 equilateral triangles. However, the first is by far the most important.
Napoleon’s theorem states that if equilateral triangles are erected on the sides of any triangle, the centers of those three triangles themselves form an equilateral triangle.
If the triangles are erected outwards, as in the image on the left, the triangle is known as the outer Napoleon triangle. Otherwise, if the triangles are erected inwards, the triangle is known as the inner Napoleon triangle. The difference between the areas of these two triangles is equal to the area of the original triangle.
The inner and outer Napoleon triangles share the same center, which is also the centroid of the original triangle.
Equilateral Triangle Formula To Find Height/altitude
The line segment from a vertex perpendicular to the opposite side is the altitude or height of an equilateral triangle. An equilateral triangles altitude bisects both its base and the opposite angle.
If you draw a height/altitude in an equilateral triangle, we can see that the triangle is divided into two right-angled triangles in which: sides \ are hypotenuses, heigh/altitude is common for both triangles, the other side is equal to \, therefore we can use the Pythagorean theorem.
\^+h^=a^\)\^\)\\\\\\
Hence, \ is the formula to find the height/altitude of an equilateral triangle.
Related Concepts:
Altitude Of An Equilateral Triangle
The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The image below shows an equilateral triangle ABC where BD is the height , AB = BC = AC, ABD = CBD, and AD = CD.
For an equilateral triangle, all angles are equal to 60°.
In triangle ADB,
We know, AB = BC = AC = s
sin 60° = h/s
Recommended Reading: Eoc Fsa Practice Test Algebra 1
Condition On The Sides
The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. That sum can equal the length of the third side only in the case of a degenerate triangle, one with collinear vertices. It is not possible for that sum to be less than the length of the third side. A triangle with three given positive side lengths exists if and only if those side lengths satisfy the triangle inequality.
Basic Properties Of An Equilateral Triangle
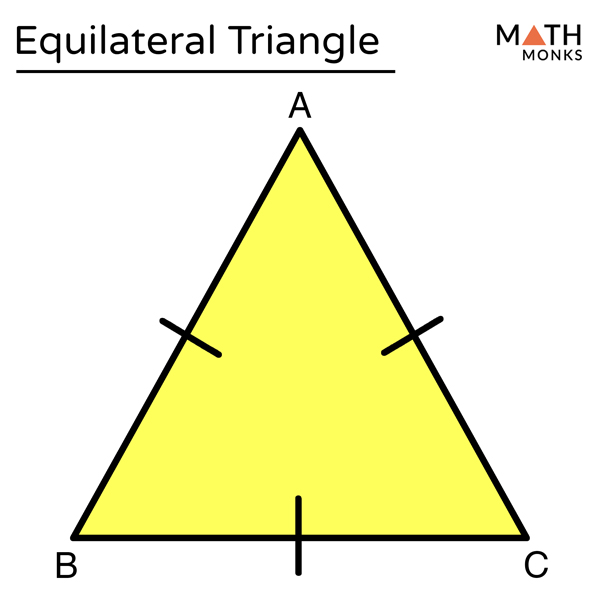
Some of the basic properties of an equilateral triangle are:
Also, Check:
Also Check: K+ Chemistry
Frequently Asked Questions : Equilateral Triangle Formula
Q.1. What is the formula of an equilateral triangle?Ans: Formula to find an area of an equilateral triangle is given by,\^ \,\text \)And, formula to find the perimeter of an equilateral triangle is given by,\, where side \ units.
Q.2. What is the formula of equilateral triangle height?Ans: Formula to find the height of an equilateral triangle is given by,\
Q.3. How do you find the length of one side of an equilateral triangle?Ans: Case -1: We can find the length of an equilateral triangle if the perimeter is given,\Case-2: We can find the length of an equilateral triangle if the area is given,\
Q.4. How to calculate the equilateral triangle height formula?Ans: If we divide the equilateral triangle into two equal parts and give the values \ and \ Consider the hypotenuse as \ and side \ will be equal to half of the side length, and side \ is the height of the equilateral triangle. Then, by using the Pythagoras theorem, we can find the height of an equilateral triangle.\where, \, \
Q.5. What is the area of an equilateral triangle formula when height is given.Ans: The formula to find the area of an equilateral triangle when the height is given is,\}\)\Where \, \
Students can access the following free study materials on Embibe for their preparation:
Different Types Of Triangles
To classify triangles according to their angles, we measure each of its interior angles. Triangles can be classified by angles, as:
|
|
|
An acute triangle has all interior angles acute , a right triangle has one right angle and an obtuse triangle has one obtuse angle .
To classify the triangles according to their sides, we measure the length of each of its sides. Triangles can be classified by their sides, as:
|
|
|
To classify triangles according to both angles and sides, we measure the interior angles and length of the sides of the triangle. Few examples of triangles classified on the basis of both angles and sides are:
|
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
What Is An Equilateral Triangle
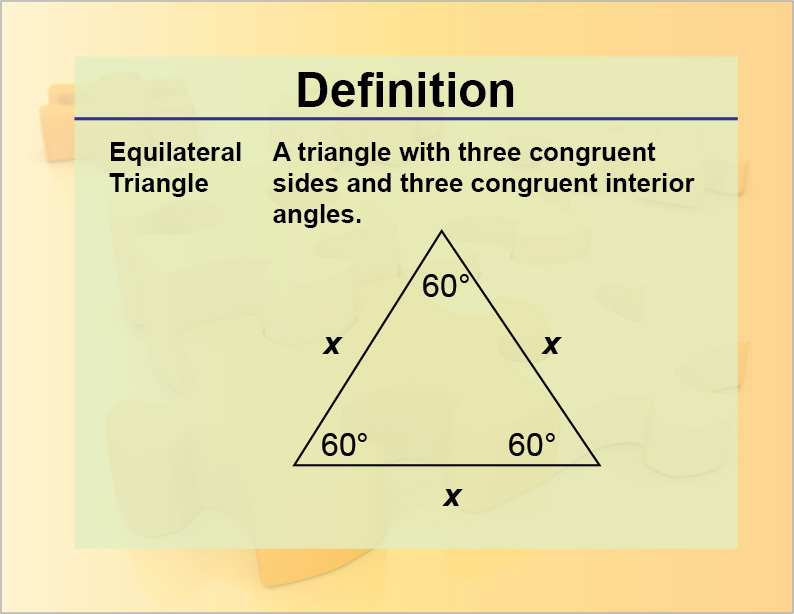
An Equilateral triangle is a triangle in which all three sides are equal and angles are also equal. The value of each angle of an equilateral triangle is 60 degrees therefore, it is also known as an equiangular triangle. The equilateral triangle is considered as a regular polygon or a regular triangle as angles are equal and sides are also equal.
The triangles are categorized into three different types based on their sides. They are isosceles triangle, scalene triangle, and equilateral triangle. The equilateral triangle is different from the isosceles and scalene triangle.
- In the scalene triangle, all the sides of the triangle are not equal and angles are also not equal.
- In the isosceles triangle, two sides are equal and the opposite angles of equal sides are equal.
- In an equilateral triangle, all sides are equal and angles are also equal.
Look at the given figure
In the given figure the sides of triangle ABC are equal i.e.AB=BC=CA = a units.
Also, A, B and, C = 60°Therefore, according to the definition of the equilateral triangle the triangle, ABC is an equilateral triangle.
Difference Between Median And Altitude Of A Triangle
| Median of triangle | Altitude of triangle |
| Median is a line segment drawn from the vertex to the middle of the opposite side of a triangle. | Altitude is drawn from the vertex and is perpendicular to the opposite side of the triangle |
| It bisects the opposite side | It may or may not bisect the opposite side, based on the type of triangle |
| It lies inside the triangle always | It may or may not lie inside the triangle, depending on the type of triangle |
| It divides the triangle into two equal parts | It does not divide the triangle into two equal parts |
| The intersection point of the three medians is called the centroid of the triangle | The intersection point of three altitudes is called the orthocenter of the triangle |
Don’t Miss: Kuta Software Infinite Geometry The Segment Addition Postulate Answer Key
Area Of Equilateral Triangle
The area of an equilateral triangle is the region occupied by it in a two-dimensional plane. The formula for the area of an equiangular triangle is given by:
A = 3a2/4
Let us derive the formula here:
If we see the above figure, the area of a triangle is given by
Area = ½ x base x height
Here Base = a and height = h
Therefore,
Area = ½ x a x h
Now, from the above figure, the altitude h bisects the base into equal halves, such as a/2 and a/2. It also forms two equivalent right-angled triangles.
So, for a right triangle, using Pythagoras theorem, we can write:
a2 = h2 + 2
| 3a/2 |
Altitudes Of Different Triangles
About altitude, different triangles have different types of altitude. Below is an overview of different types of altitudes in different triangles.
For an obtuse-angled triangle, the altitude is outside the triangle. For such triangles, the base is extended, and then a perpendicular is drawn from the opposite vertex to the base. For an obtuse triangle, the altitude is shown in the triangle below.
Read Also: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Equilateral Triangle Formula To Find Area: Herons Formula
Herons formula or Heros formula can be used to derive a special formula applicable to calculate the area of an equilateral triangle only.
In an equilateral triangle, the lengths of all the sides are the same. So, \.
Therefore, \
So, the area \ \times\left \times\left}\)
\, where the length of the side of the triangle is \.
Therefore, the area of an equilateral triangle is \^\).
Figures Circumscribed About A Triangle
The tangential triangle of a reference triangle is the triangle whose sides are on the tangent lines to the reference triangle’s circumcircle at its vertices.
As mentioned above, every triangle has a unique circumcircle, a circle passing through all three vertices, whose center is the intersection of the perpendicular bisectors of the triangle’s sides.
Further, every triangle has a unique Steiner circumellipse, which passes through the triangle’s vertices and has its center at the triangle’s centroid. Of all ellipses going through the triangle’s vertices, it has the smallest area.
The Kiepert hyperbola is the unique conic which passes through the triangle’s three vertices, its centroid, and its circumcenter.
Of all triangles contained in a given convex polygon, there exists a triangle with maximal area whose vertices are all vertices of the given polygon.
Don’t Miss: College Algebra 6th Edition Dugopolski Pdf
Medians Angle Bisectors Perpendicular Side Bisectors And Altitudes
The medians and the sides are related by:p.70
- 3
- 3 T \cdot a=q_\cdot b=q_\cdot c=}T\,}
for area T.
Carnot’s theorem states that the sum of the distances from the circumcenter to the three sides equals the sum of the circumradius and the inradius.:p.83 Here a segment’s length is considered to be negative if and only if the segment lies entirely outside the triangle. This method is especially useful for deducing the properties of more abstract forms of triangles, such as the ones induced by Lie algebras, that otherwise have the same properties as usual triangles.
Euler’s theorem states that the distance d between the circumcenter and the incenter is given by:p.85
- d
- , }+}=},}
where R is the circumradius and r is the inradius. Thus for all triangles R 2r, with equality holding for equilateral triangles.
If we denote that the orthocenter divides one altitude into segments of lengths u and v, another altitude into segment lengths w and x, and the third altitude into segment lengths y and z, then uv = wx = yz.:p.94
The distance from a side to the circumcenter equals half the distance from the opposite vertex to the orthocenter.:p.99
The sum of the squares of the distances from the vertices to the orthocenter H plus the sum of the squares of the sides equals twelve times the square of the circumradius::p.102
- A
- A .
Sine Cosine And Tangent Rules
The law of sines, or sine rule, states that the ratio of the length of a side to the sine of its corresponding opposite angle is constant, that is
- a . }=}=}.}
This ratio is equal to the diameter of the circumscribed circle of the given triangle. Another interpretation of this theorem is that every triangle with angles , and is similar to a triangle with side lengths equal to sin , sin and sin . This triangle can be constructed by first constructing a circle of diameter 1, and inscribing in it two of the angles of the triangle. The length of the sides of that triangle will be sin , sin and sin . The side whose length is sin is opposite to the angle whose measure is , etc.
The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As per the law:
For a triangle with length of sides a, b, c and angles of , , respectively, given two known lengths of a triangle a and b, and the angle between the two known sides , to calculate the third side c, the following formula can be used:
- c
- ] . }=}.}
Read Also: How To Find Ksp Chemistry
Examples Of Equilateral In A Sentence
equilateral Forbesequilateral Quanta Magazineequilateral Quanta Magazineequilateral WSJequilateral Quanta Magazineequilateral Scientific Americanequilateral Popular Mechanicsequilateral oregonlive
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘equilateral.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Properties Of Equilateral Triangle
An equilateral triangle has some properties which define a triangle as an equilateral triangle. Follow the below properties for the identification of an equilateral triangle.
- sides of an equilateral triangle are equal in measurements.
- angles are congruent of an equilateral triangle and are equal to 60 degrees.
- a regular polygon because it has three sides.
- the perpendicular drawn from any of the vertex to the opposite side of an equilateral triangle bisects the side in equal lengths. It also bisects the angle of the vertex into equal halves i.e. 30 degrees each from where the perpendicular is drawn.
- Ortho-centreand centroid are at the same point.
- median, angle bisector,and altitude of an equilateral triangle for all sides are the same.
- area of an equilateral triangle = 3a2/ 4, here a = side of an equilateral triangle
- perimeter of an equilateral triangle = 3a, here a = side of an equilateral triangle
- The sum of all the angles of an equilateral triangle is equal to 180 degrees.
Read Also: Scientific Definition Of Abiotic
Points Lines And Circles Associated With A Triangle
There are thousands of different constructions that find a special point associated with a triangle, satisfying some unique property: see the article Encyclopedia of Triangle Centers for a catalogue of them. Often they are constructed by finding three lines associated in a symmetrical way with the three sides and then proving that the three lines meet in a single point: an important tool for proving the existence of these is Ceva’s theorem, which gives a criterion for determining when three such lines are concurrent. Similarly, lines associated with a triangle are often constructed by proving that three symmetrically constructed points are collinear: here Menelaus’ theorem gives a useful general criterion. In this section just a few of the most commonly encountered constructions are explained.
A perpendicular bisector of a side of a triangle is a straight line passing through the midpoint of the side and being perpendicular to it, i.e. forming a right angle with it. The three perpendicular bisectors meet in a single point, the triangle’s circumcenter, usually denoted by O this point is the center of the circumcircle, the circle passing through all three vertices. The diameter of this circle, called the circumdiameter, can be found from the law of sines stated above. The circumcircle’s radius is called the circumradius.
The center of the incircle is not in general located on Euler’s line.
Definition Of An Equilateral Triangle
As we mentioned in the introduction, an equilateral triangle is a triangle that has all sides of equal lengths. Also, the three interior angles of an equilateral triangle are also congruent and equal to 60 degrees. The following is a diagram of an equilateral triangle:
In the equilateral triangle ABC, we have the following:
where AB, BC, and AC are the sides of the triangle. And we also have:
Don’t Miss: Geometry Segment Addition Postulate Worksheet
Internal Angles Of A Convex Equilateral Pentagon
When a convex equilateral pentagon is dissected into triangles, two of them appear as isosceles while the other one is more general . We assume that we are given the adjacent angles .
According to the law of sines the length of the line dividing the green and blue triangles is:
- a }\right).}
The square of the length of the line dividing the orange and green triangles is:
- b ) . b^& =1+a^-2\cos \left\\& =1+4\sin ^\left-4\sin \left\sin \left.\\\end}}
According to the law of cosines, the cosine of can be seen from the figure:
- cos +1^-b^}}\ .}
Simplifying, is obtained as function of and :
- .
The remaining angles of the pentagon can be found geometrically: The remaining angles of the orange and blue triangles are readily found by noting that two angles of an isosceles triangle are equal while all three angles sum to 180°. Then , and the two remaining angles of the green triangle can be found from four equations stating that the sum of the angles of the pentagon is 540°, the sum of the angles of the green triangle is 180°, the angle is the sum of its three components, and the angle is the sum of its two components.
A cyclic pentagon is equiangularif and only if it has equal sides and thus is regular. Likewise, a tangential pentagon is equilateral if and only if it has equal angles and thus is regular.