Different Types Of Sample Spaces In Probability
In probability, sample space is a set of all possible outcomes of an experiment.
A sample space can be finite or infinite.
A sample space can be discrete or continuous.
A sample space can be countable or uncountable.
From some texts I got that finite sample space is same as discrete sample space and infinite sample space is continuous sample space.
But some texts are saying that countable sample space is discrete sample space and uncountable sample space is continuous sample space.
Which one of the following above is correct?
I got confuse because of the following two statements in this text book
Discrete Probability Law :
If the sample space consists of a finite number of possible outcomes, then theprobability law is specified by the probabilities of the events that consist ofa single element. In particular, the probability of any event $\$is the sum of the probabilities of its elements.
Continuous Models :
Probabilistic models with continuous sample spaces differ from their discretecounterparts in that the probabilities of the single-element events may not besufficient to characterize the probability law.
Discrete probability law deals with finite sample spaces, but continuous probability models deal with continuous sample spaces. So I am confused whether countably finite sample spaces comes under which probabilistic model.
listen this also for accuracy.
Convenient Strategies To Determine A Sample Space
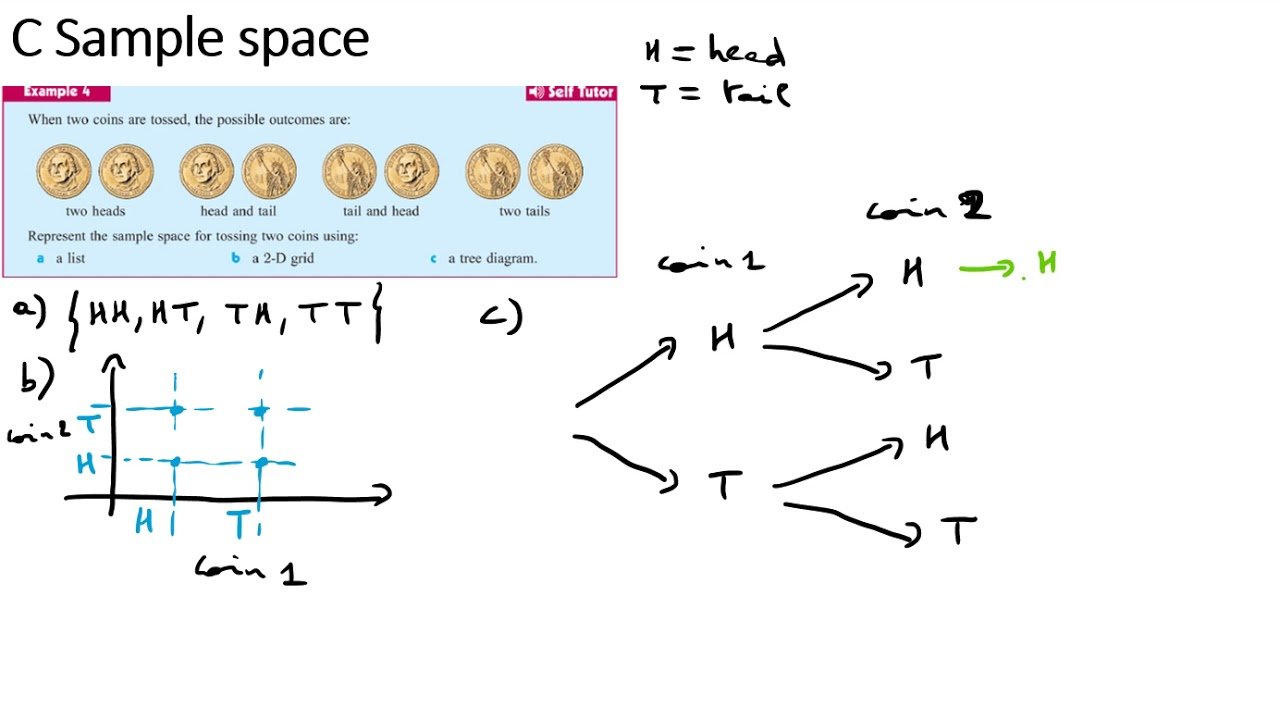
There are strategies that can be used to avoid missing some of the possible outcomes when writing out the sample space. In this section we will look at charts , and tree diagrams.;
Chart
A chart is set up using rows and columns like a table. It is typically used to determine the sample space of an experiment that combines two activities. Observe the example below.
Experiment 4: Simultaneously tossing two dice
| ; |
This chart correctly shows the 36 outcomes in this sample space.
Tree Diagram
We can also use a tree diagram to find the sample space of an experiment. The branches show combinations of results of separate activities that make up an outcome.;
Experiment 5: Flipping a coin and tossing a die
From this diagram we can read off the 12 possible outcomes in the sample space as:
Notice that the order here does not matter. We do not count, for example, H1 as a different outcome from 1H.
Infinitely Large Sample Spaces
In an elementary approach to probability, any subset of the sample space is usually called an event. However, this gives rise to problems when the sample space is continuous, so that a more precise definition of an event is necessary. Under this definition only measurable subsets of the sample space, constituting a -algebra over the sample space itself, are considered events.
An example of an infinitely large sample space is measuring the lifetime of a light bulb. The corresponding sample space would be
Read Also: What Is Copulation In Biology
What Are Equally Likely Events
When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:
- Getting 3 and 5 on throwing a die
- Getting an even number and an odd number on a die
- Getting 1, 2 or 3 on rolling a die
are equally likely events, since the probabilities of each event are equal.
Probability With Binomial Coefficients
The examples given thus far have had relatively small sample spaces. For small sample spaces, it’s a simple exercise to list out all possible outcomes, and then count the size of the sample space and the events in it. However, it is common for sample spaces to be too large to list exhaustively. The binomial coefficient can often be used to count the sizes of large sample spaces and events without having to list out outcomes.
Problems involving a standard playing card deck typically use binomial coefficients to find the size of sample spaces and events.
A standard playing card deck, also called a poker deck, contains 52 distinct cards.
These cards are divided into four suits:
Hearts and Diamonds are the two red suits. These are sometimes abbreviated as H and D.
Clubs and Spades are the two black suits. These are sometimes abbreviated as C and S.
There are 13 ranks in each suit: An Ace, nine cards numbered 2
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Infinite Discrete Sample Spaces
First tail. The experiment is to repeatedly toss a coin until first tail shows up. Possible outcomes are sequences of H that, if finite, end with a single T, and an infinite sequence of H:
As we shall see elsewhere, this is a remarkable space that contains a not impossible event whose probability is 0. One random variable is defined most naturally as the length of an outcome. It draws values from the set of whole numbers augmented by the symbol of infinity:
Discrete Distributions: Probability Mass
When the sample space consists of discrete outcomes, then we can talk about the probability of each distinct outcome. For example, the sample space of a flipped coin has two discrete outcomes, and we talk about the probability of head or tail. The sample space of a six-sided die has six discrete outcomes, and we talk about the probability of 1 dot, 2 dots, and so forth.
For continuous outcome spaces, we can discretize the space into a finite set of mutually exclusive and exhaustive bins. For example, although heights of people are a continuous scale, we can divide the scale into a finite number of intervals, such as < 51, 51 to 53, 53 to 55, 55 to 57, , > 83. Then we can talk about the probability that a randomly selected person falls into any of those intervals. Suppose that we randomly sample 10,000 people and measure the heights very accurately. The top panel of Figure 4.2 shows a scatter plot of the 10,000 measurements, with vertical dashed lines marking the intervals. In particular, the number of measurements that fall within the interval 63 to 65 is 1,473, which means that the probability of falling in that interval is 1,473/10, 000 = 0.1473.
Figure 4.2. Examples of computing probability density. Within each main panel, the upper plot shows a scatter of 10,000 heights of randomly selected people, and the lower plot converts into probability density for the particular selection of bins depicted.
S.J. Garrett, in, 2015
Also Check: Who Are Paris Jackson’s Biological Parents
Probability Definition In Math
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e. how likely they are to happen, using it. Probability can range in from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.
For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible . But if we toss two coins in the air, there could be three possibilities of events to occur, such as both the coins show heads or both show tails or one shows heads and one tail, i.e., ,.
Probability Of An Event
Assume an event E can occur in r ways out of a sum of n probable or possible equally likely ways. Then the probability of happening of the event or its success; is expressed as;
P = r/n
The probability that the event will not occur or known as its failure is expressed as:
P = /n = 1-
E represents that the event will not occur.
Therefore, now we can say;
P + P = 1
This means that the total of all the probabilities in any random test or experiment is equal to 1.
Read Also: What Are Dyes In Chemistry
How Do We Find A Sample Space
To determine the sample space of an experiment, we list ALL the possible outcomes of the experiment.
You may have noticed that the sample space is found by listing all the possible outcomes of the experiment. Lets now look at some cases where the sample space is not as obvious.
Experiment 2: Picking one fruit from a basket with 3 apples, 5 pears, 2 bananas, and 1 orange.
Notice that the number of individual fruits did not affect the total number of possible outcomes. This is because this experiment is one where we pick a single fruit from the basket. Here we can pick either an apple, a pear, a banana, or an orange. We cannot pick a fruit the basket does not contain, and we are only picking one fruit.
What if we now wanted to pick two fruits from the basket?
Experiment 3:Picking two fruits from a basket with 3 apples, 5 pears, 2 bananas, and 1 orange
To simplify our sample space, we will use:
A Apple ;
B Banana
O Orange
Observe that we cannot choose from the basket since there is only one orange in the basket. Additionally, since we are picking the fruits at the same time is the same as . Thus, the outcome of choosing an apple and a pear occurs just once in the sample space.
Determining The Number Of Outcomes In A Sample Space
In experiments 14 and 15, we mapped the possible outcomes of the unique activities with each other on a one-to-one basis. As a result, the number of outcomes of the experiment was the product of the number of outcomes of the two activities. This observation is useful when it is not practical to write out all the elements in a sample space.
For example, flipping a coin has 2 items in its sample space. Rolling a die has 6. Thus, the sample space of the experiment from simultaneously flipping a coin and rolling a die consisted of:
2 × 6 = 12 possible outcomes.
You May Like: How Do Noise Cancelling Headphones Work Physics
Tossing A Fair Coin 2
Consider the experiment of tossing a coin twice. The possible outcomes are as follows:
Event
-
toss .
Thus, the sample space S consists of the simple events A, B, C, and D. Again, using set notation we can write the sample space as follows:
The sample space may be viewed symbolically in terms of the Venn diagram. The sample space of Example 5.3.6 is shown by Figure 5.1.
Figure 5.1. Venn diagram for Example 5.3.6.
Having constructed the sample space, we can formulate additional events by grouping the necessary sample points. That is, in Example 5.3.6 the event of obtaining either two heads or two tails will consist of the simple events A and D. This event is represented on the Venn diagram by circling the sample points A and D, as shown by the enclosed` portion of S in Figure 5.1.
Examples Of Sample Space
Tossing A Coin: When we toss a coin, there can be only two outcomes i.e., either head or tail. So the sample space will be, S = where H is the head and T is the tail.;
Tossing Two Coins Together: When we flip two coins together, we have a total of 4 outcomes. H1 and T1 can be represented as heads and tails of the first coin. And H2 and T2 can be represented as heads and tails of the second coin. So the sample space will be, S = ;
With this, we know that if we have n coins, the possible number of outcomes will be 2n.;;;
Rolling A Dice: On rolling a die, we can have 6 outcomes. So the sample space will be, S = ;;;;
Rolling Two Dice Together: When we roll two dice together, we get double the outcomes than when we roll a single outcome. When we roll 1 dice, we get 6 outcomes and when we roll 2 dice together we get 36 outcomes So the possible sample space will be, S = { , . If we throw three dice together, we should have the possible outcomes of 216. Here n in the experiment will be taken as 3, so it becomes 63 = 216.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;Image will be uploaded
In the same way, there are many events where we use the method of sample space such as while playing cards or even while deciding something. We can use it in many games too.;;
Also Check: People Who Are Always Late Psychology
What Is A Sample Space
There are lots of events like when we toss a coin or toss a die and we cannot predict the outcomes with certainty but we can always say all the possible outcomes. These events are what we call a random phenomenon or a random experiment. Probability theory is usually involved with such random phenomena or random experiments. But what is a sample space?; A sample space is a collection or a set of all such possible outcomes is known as a sample space of the experiment and is normally denoted by S. it may have a number of outcomes that usually depends on ob the experiment but if it has a finite set of numbers, then it is called a discrete or finite sample space.
Now, we have two more questions. First, what is the probability? And what are events? We got you! Here is the answer.;
Definitions Of Key Terms
A probability experiment is something that has an uncertain result. In the context of probability, this is often just referred to as an experiment.
An experiment could be rolling a fair 6-sided die, or flipping a fair coin. In either case, the result is random, and we cannot predict what it will be. In the field of science, we often think of “experiments” as things that we control in a lab. However, in probability theory, an experiment need not be something that we control. For example, a probability experiment could be the weather tomorrow.
Even though it’s not possible to know what the result of an experiment will be, it can be very helpful to analyze and understand what could possibly happen. Something that could possibly happen is called an outcome.
An outcome is a possible result of an experiment.
A possible outcome of rolling a fair 6-sided die is 4 4 4. A possible outcome of flipping a fair coin is “heads.” Both of these experiments have relatively few possible outcomes, and so it is easy to think of all the possible outcomes. However, there are some experiments with relatively massive amounts of potential outcomes. Think of a lottery as a probability experiment. There are millions of potential winners in a lottery, and so there are millions of potential outcomes of the experiment. It would be very difficult to consider every possible winner of the lottery individually.
The set of all outcomes in an experiment is called the sample space of that experiment.
Recommended Reading: Math Caching Algebra 1 Answers
Forming Other Sample Spaces
The above list includes some of the most commonly used sample spaces. Others are out there for different experiments. It is also possible to combine several of the above experiments. When this is done, we end up with a sample space that is the Cartesian product of our individual sample spaces. We can also use a tree diagram to form these sample spaces.
For example, we may want to analyze a probability experiment in which we first flip a coin and then roll a die.;Since there are two outcomes for flipping a coin and six outcomes for rolling a die, there are a total of 2 x 6 = 12 outcomes in the sample space we are considering.
What Is Sample Space
Definition:;The;sample space;of an experiment is the set of all possible outcomes of that experiment.
Experiment 1:;What is the probability of each outcome when a dime is tossed?
Outcomes:;The outcomes of this experiment are head and tail.
Probabilities:;
| 2 |
The sample space of Experiment 1 is: ;;
Experiment 2:;A spinner has 4 equal sectors colored yellow, blue, green and red. What is the probability of landing on each color after spinning this spinner?
Sample Space:;
Probabilities:
| 1 |
| 4 |
Experiment 3:;What is the probability of each outcome when a single 6-sided die is rolled?
Sample Space:;
Probabilities:;
| 1 |
| 6 |
Experiment 4:;A glass jar contains 1 red, 3 green, 2 blue and 4 yellow marbles. If a single marble is chosen at random from the jar, what is the probability of each outcome?
Sample Space:;
Probabilities:;
| 10 | 5 |
Summary:;The sample space of an experiment is the set of all possible outcomes for that experiment. You may have noticed that for each of the experiments above, the sum of the probabilities of each outcome is 1. This is no coincidence.;The sum of the probabilities of the distinct outcomes within a sample space is 1.
The sample space for choosing a single card at random from a deck of 52 playing cards is shown below. There are 52 possible outcomes in this sample space.
The probability of each outcome of this experiment is:
| P |
Recommended Reading: Eoc Fsa Warm Ups Algebra 1 Answers
Sample Spaces And Events
Rolling an ordinary six-sided die is a familiar example of a random experiment, an action for which all possible outcomes can be listed, but for which the actual outcome on any given trial of the experiment cannot be predicted with certainty. In such a situation we wish to assign to each outcome, such as rolling a two, a number, called the probability of the outcome, that indicates how likely it is that the outcome will occur. Similarly, we would like to assign a probability to any event, or collection of outcomes, such as rolling an even number, which indicates how likely it is that the event will occur if the experiment is performed. This section provides a framework for discussing probability problems, using the terms just mentioned.
Definition: random experiment
A random experimentis a mechanism that produces a definite outcome that cannot be predicted with certainty. The sample space associated with a random experiment is the set of all possible outcomes. An event is a subset of the sample space.
Definition: Element and Occurrence
An event \ is said to occur on a particular trial of the experiment if the outcome observed is an element of the set \.
Example \: Sample Space for a single coin
Construct a sample space for the experiment that consists of tossing a single coin.
Solution
The outcomes could be labeled \ for heads and\for tails. Then the sample space is the set: \
Example \: Sample Space for a single die
Solution:
Example \: Sample Spaces for two coines
: