Section22vector Equations And Spans Permalink
Objectives
An equation involving vectors with n coordinates is the same as n equations involving only numbers. For example, the equation
For two vectors to be equal, all of their coordinates must be equal, so this is just the system of linear equations
Definition
A vector equation is an equation involving a linear combination of vectors with possibly unknown coefficients.
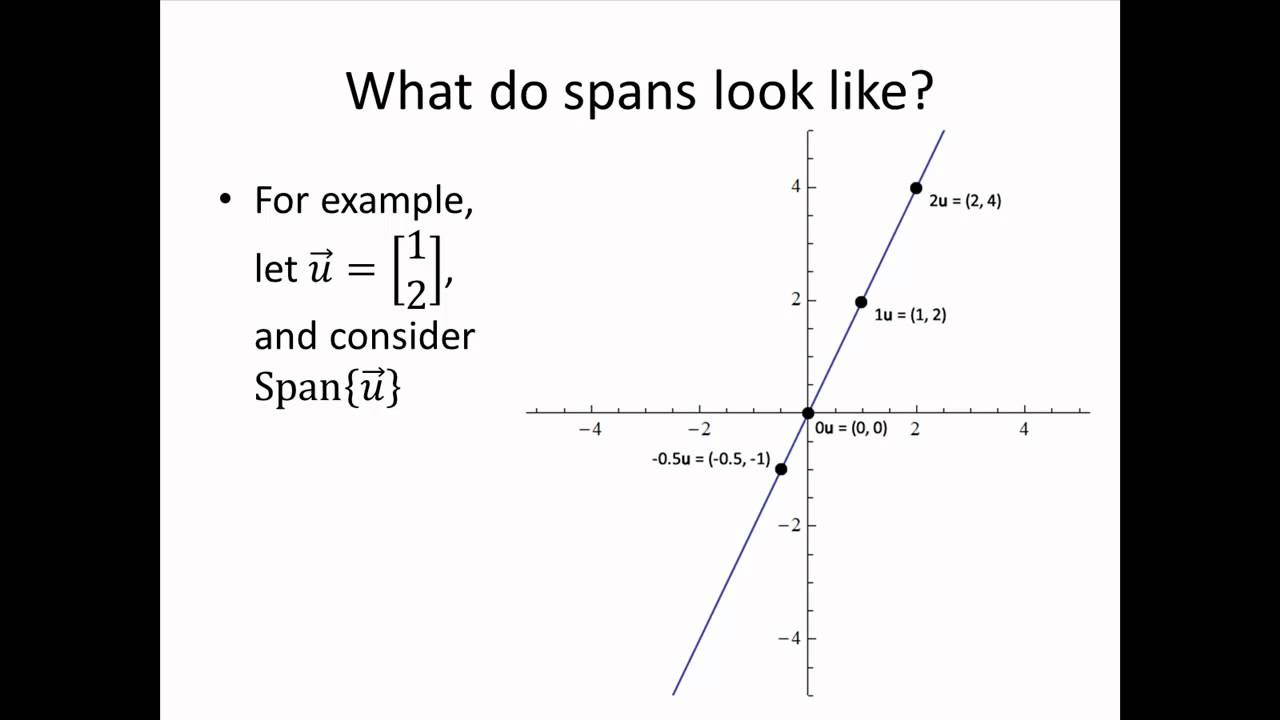
Asking whether or not a vector equation has a solution is the same as asking if a given vector is a linear combination of some other given vectors.
For example the vector equation above is asking if the vector .
The thing we really care about is solving systems of linear equations, not solving vector equations. The whole point of vector equations is that they give us a different, and more geometric, way of viewing systems of linear equations.
A Picture of a Consistent System
In order to actually solve the vector equation
one has to solve the system of linear equations
This means forming the augmented matrix
Recipe: Solving a vector equation
In general, the vector equation
are unknown scalars, has the same solution set as the linear system with augmented matrix
Basis For A Row Space
- Input An m;×;n matrix A.
- Output A basis for the row space of A.
- Use elementary row operations to put A into row echelon form.
- The nonzero rows of the echelon form are a basis for the row space of A.
See the article on row space for an example.
If we instead put the matrix A into reduced row echelon form, then the resulting basis for the row space is uniquely determined. This provides an algorithm for checking whether two row spaces are equal and, by extension, whether two subspaces of Kn are equal.
A Linear Span Is A Linear Space
The following proposition, although elementary, is extremely important.
Proposition The linear span of a set of vectors is a linear space.
be the linear span of vectors is the set of all vectors that can be represented as linear combinationsTake two vectors is a linear space if and only if, for any two coefficients andcan itself be expressed as a linear combination of the vectors with coefficients. As a consequence, it belongs to the span. In summary, we have proved that any linear combination of vectors belonging to the span also belongs to the span. This means that
Below you can find some exercises with explained solutions.
You May Like: Homework 5 Angle Addition Postulate Answer Key
Basis For A Column Space
- Input An m;×;n matrix A
- Output A basis for the column space of A
- Use elementary row operations to put A into row echelon form.
- Determine which columns of the echelon form have pivots. The corresponding columns of the original matrix are a basis for the column space.
See the article on column space for an example.
This produces a basis for the column space that is a subset of the original column vectors. It works because the columns with pivots are a basis for the column space of the echelon form, and row reduction does not change the linear dependence relationships between the columns.
The Definition Of Span

In Linear Algebra by Friedberg, Insel and Spence, the definition of span is given as:
Let $S$ be a nonempty subset of a vector space $V$. The span of $S$, denoted by span$$, is the set containing of all linear combinations of vectors in $S$. For convenience, we definespan$=\$.
In Linear Algebra by Hoffman and Kunze, the definition of span is given as:
Let $S$ be a set of vectors in a vector space $V$. The subspace spanned by $S$ is defined to be intersection $W$ of all subspaces of $V$ which contain $S$. When $S$ is finite set of vectors, $S =\$, we shall simply call $W$ the subspace spanned by the vectors $\alpha_1, \alpha_2, …, \alpha_n$.
I am not able to understand the second definition completely. How do I relate “set of all linear combinations” and “intersection $W$ of all subspaces”? Please help.
Thanks.
- 2$\begingroup$Note that in the first definition $S$ is a nonempty set, and the span of the empty set has to be defined as a special case. The second definition works when $S$ is empty, since every subspace of $V$ considered as a set includes the empty set, and $\$ is the smallest subspace of any vector space. If you use the first definition directly to prove other results, you will probably have to consider that “special case” separately in every proof.$\endgroup$
Let $$,…, \in V\;$$ then we define the space spanned by $$,…,$$ as $$S\left = \left\^n \;|\; \in \mathbb} } \right\}$$ which is the set of all linear combinations of the vectors in this subspace.
Don’t Miss: Segment Addition Postulate Find The Length Indicated
Linearly Dependent & Independent
- Linear dependence: two vectors are COLLINEAR, means on the same line.
- Linear independence: two vectors are NOT COLLINEAR, means they’re not on the same line.
Vectors and are the SAME VECTOR! Because = 2*, so it’s just a scaled version of the first vector.
So we say the vectors and are DEPENDENT, because they’re COLLINEAR.
Other than that, any two vectors are INDEPENDENT, if they’re not NOT COLLINEAR.
Understanding The Difference Between Span And Basis
I’ve been reading a bit around MSE and I’ve stumbled upon some similar questions as mine. However, most of them do not have a concrete explanation to what I’m looking for.
I understand that the Span of a Vector Space $V$ is the linear combination of all the vectors in $V$.
I also understand that the Basis of a Vector Space V is a set of vectors $, v_, …, v_}$ which is linearly independent and whose span is all of $V$.
Now, from my understanding the basis is a combination of vectors which are linearly independent, for example, $$ and $$.
But why?
The other question I have is, what do they mean by “whose span is all of $V$” ?
On a final note, I would really appreciate a good definition of Span and Basis along with a concrete example of each which will really help to reinforce my understanding.
Thanks.
- 2$\begingroup$Here is a lecture from Gilbert Strang about Span and Basis. His explanation is very good, so posting the video here instead of instead of answering it again. All the sessions around Linear Algebra can be found here.$\endgroup$
Span is usually used for a set of vectors. The span of a set of vectors is the set of all linear combinations of these vectors.
So the span of $\1\\0\end, \begin0\\1\end\}$ would be the set of all linear combinations of them, which is $\mathbb^2$. The span of $\2\\0\end, \begin1\\0\end, \begin0\\1\end\}$ is also $\mathbb^2$, although we don’t need $\begin2\\0\end$ to be so.
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Introduction To Linear Algebra
Linear algebra is the study of linear combinations. It is the study of vector spaces, lines and planes, and some mappings that are required to perform the linear transformations.; It includes vectors, matrices and linear functions. It is the study of linear sets of equations and its transformation properties.
Linear Algebra Equations
The general linear equation is represented as
a1x1 + a2x2.+anxn = b
as represents the coefficients
xs represents the unknowns
b represents the constant
There exists a system of linear algebraic equations, which is the set of equations. The system of equations can be solved using the matrices.
It obeys the linear function such as
a1x1 +.+anxn
The most important topics covered in the linear algebra includes:
- Euclidean vector spaces
- Singular value decomposition
- Linear dependence and independence
Here, the three main concepts which are the prerequisite to linear algebra are explained in detail. They are:
- Vector spaces
- Linear Functions
- Matrix
All these three concepts are interrelated such that a system of linear equations can be represented using these concepts mathematically. In general terms, vectors are elements that we can add, and linear functions are the functions of vectors that include the addition of vectors
Basis For A Null Space
- Input An m;×;n matrix A.
- Output A basis for the null space of A
- Use elementary row operations to put A in reduced row echelon form.
- Using the reduced row echelon form, determine which of the variables x1, x2, …, xn are free. Write equations for the dependent variables in terms of the free variables.
- For each free variable xi, choose a vector in the null space for which xi = 1 and the remaining free variables are zero. The resulting collection of vectors is a basis for the null space of A.
See the article on null space for an example.
Read Also: Fsa Algebra 1 Eoc Answer Key
How To Calculate A Linear Combination’s Independency
Its important for knowing if a linear combination can fill out a plane or space. For example, if two vectors aren’t independent, then it’s just one vector, and can only draw a line. If three vectors aren’t independent, then they’re just two vectors, one is redundant, so they can only fill out a 2D plane instead of a 3D space.
A linear combination is independent, iff it could satisfy this equation:
cv + cv + cv .... = 0
c.. means the scalar for each vector, and you could change the scalar to any number, positive or negative.Note that: c 0, and vectors are not all zeros.
Assume that theres a linear combination of two vectors v + v + v, with scalars it could be cv + cv + cv.To verify whether it’s dependent or independent, we assume cv + cv + cv= and solve for c, c, c:
- its independent<=> if c = c = c = 0all are zeros
- its dependent<=> If c, c, cat least one is NON-ZERO number
Independent Example:
Vector Spaces And Linear Combinations
It can be seen from the definition of a vector space thatif \ are vectors from a vector space \,then \ contains every linear combination of \.So \ contains the span of \., let \and let \ and \ be scalars.Since \ is closed under scalar multiplication,we have \.Now using that \ is closed under addition,we get that \.Hence, \ contains the span of \.)
One can check that the span of \is again vector space, giving a subspace of \.
For example, let \ be given by the span of\ with real numbers as scalars.Then \ gives a vector space in which every vector isof the form\ where \ can be any real number.Note that every vector in \ is also a vector in\ but \.So \ is a proper subspace of \.
When a given vector space \is equal to \\) for some \,we have a succinct and concrete description of all the vectors in \because every vector in \ is a linear combination of these \ vectors.This is a rather attractive property that will be explored in more details.However, we will see that not every vector space can be writtenas the span of a finite set of vectors.
Also Check: Geometry Segment Addition Postulate Worksheet
Practice Problems On Linear Algebra
For more related articles on the system of linear equations, register with BYJUS The Learning app and watch interactive videos.
Coordinates For A Vector
- Input A basis for a subspace S of Kn, and a vector v S
- Output Numbers t1, t2, …, tk such that v = t1b1 + ··· + tkbk
- Create an A whose columns are b1,…,bk , with the last column being v.
- Use elementary row operations to put A into reduced row echelon form.
- Express the final column of the reduced echelon form as a linear combination of the first k columns. The coefficients used are the desired numbers t1, t2, …, tk.
If the final column of the reduced row echelon form contains a pivot, then the input vector v does not lie in S.
Don’t Miss: Lesson 1.7 Practice A Geometry Answers
Independence Basis And Dimension
Linear independenceBasis Dimension uvR
In general, a subspace of Kn determined by k parameters has dimension k. However, there are exceptions to this rule. For example, the subspace of K3 spanned by the three vectors , , and is just the xz-plane, with each point on the plane described by infinitely many different values of t1, t2, t3.
In general, vectors v1,;…;,;vk are called linearly independent if
- t v k \mathbf _+\cdots +t_\mathbf _\;\neq \;u_\mathbf _+\cdots +u_\mathbf _}
for; .If v1, …, vk are linearly independent, then the coordinatest1, …, tk for a vector in the span are uniquely determined.
A basis for a subspace S is a set of linearly independent vectors whose span is S. The number of elements in a basis is always equal to the geometric dimension of the subspace. Any spanning set for a subspace can be changed into a basis by removing redundant vectors .
- Example
- . ,t_,5t_,t_)=t_+t_.}
- The subspace S is two-dimensional. Geometrically, it is the plane in R4 passing through the points , , and .
Know If A Vector Is In The Span
How to know if a vector is in the Span ?
Let<math>A =\begin\begin&& \\v_1 & \dots & v_n \\&&\end\end</math>
Using the linear-combinations interpretation of matrix-vector multiplication, a vector x in Span can be written Ax.
Thus testing if b is in Span is equivalent to testing if the matrix equation Ax = b has a solution.
You May Like: How To Login To Imagine Math
Equations For A Subspace
- Input A basis for a subspace S of Kn
- Output An ;×;n matrix whose null space is S.
- Create a matrix A whose rows are b1, b2, …, bk.
- Use elementary row operations to put A into reduced row echelon form.
- Let c1, c2, …, cn be the columns of the reduced row echelon form. For each column without a pivot, write an equation expressing the column as a linear combination of the columns with pivots.
- This results in a homogeneous system of n k linear equations involving the variables c1,…,cn. The × n matrix corresponding to this system is the desired matrix with nullspace S.
- Example