Glossary Of Mathematical Symbols
| It has been suggested that List of mathematical symbols by subject be merged into this article. Proposed since January 2021. |
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.
The most basic symbols are the , and the letters of the Latin alphabet. The decimal digits are used for representing numbers through the HinduArabic numeral system. Historically, upper-case letters were used for representing points in geometry, and lower-case letters were used for variables and constants. Letters are used for representing many other sort of mathematical objects. As the number of these sorts has dramatically increased in modern mathematics, the Greek alphabet and some Hebrew letters are also used. In mathematical formulas, the standard typeface is italic type for Latin letters and lower-case Greek letters, and upright type for upper case Greek letters. For having more symbols, other typefaces are also used, mainly boldface a
Average Rate Of Change
The average rate of change between two input values is the total change of the function values divided by the change in the input values.
Average rate of change = =
Example 7.3 A: Cost Functions
Using the cost-of-gas function from earlier, find the average rate of change between 2007 and 2009.
From the table, in 2007 the cost of gas was $2.64. In 2009 the cost was $2.14.
The input has changed by 2. The output has changed by $2.14 $2.64 = -0.50.
The average rate of change is then dollars per year
1. Using the same cost-of-gas function, find the average rate of change between 2003 and 2008
Notice that in the last example the change of output was negative since the output value of the function had decreased. Correspondingly, the average rate of change is negative.
Example 7.3 B: Average Rate of Change
Given the function
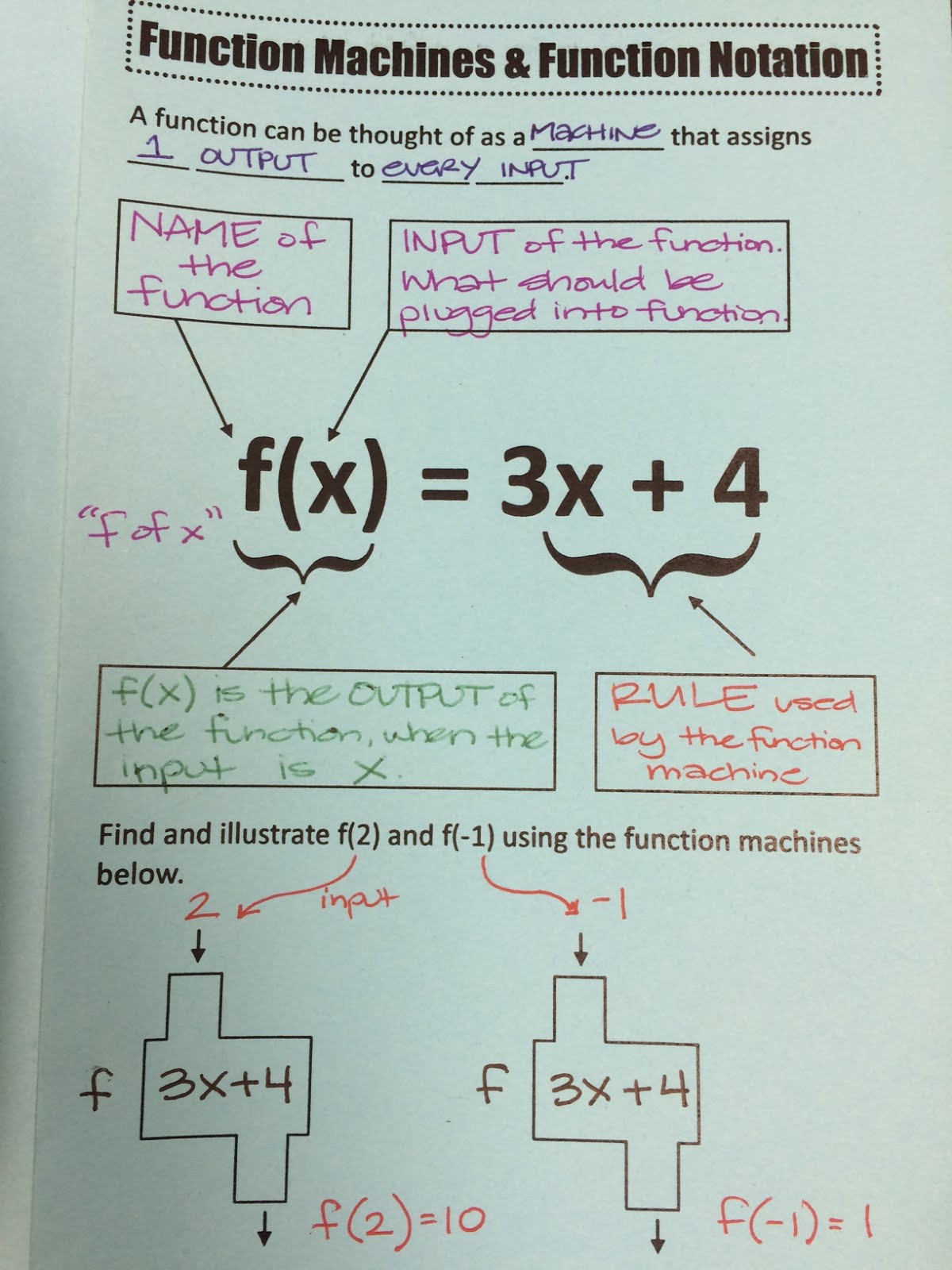
What Is A Function Notation
Notation can be defined as a system of symbols or signs that denote elements such as phrases, numbers, words etc.
Therefore, function notation is a way in which a function can be represented using symbols and signs. Function notation is a simpler method of describing a function without a lengthy written explanation.
The most frequently used function notation is f which is read as f of x. In this case, the letter x, placed within the parentheses and the entire symbol f, stand for the domain set and range set respectively.
Although f is the most popular letter used when writing function notation, any other letter of the alphabet can also be used either in upper or lower case.
Don’t Miss: Geometry Wars 2 Smile Achievement
Function / Map Notation
Please forgive my ignorance, if I’ve phrased my question improperly. I’m not sure what the appropriate terminology is; that’s the basis of my question. So, I’m not sure if I’m even remotely close in my description of this notation:
I’m wondering what is the proper name for the following notation. Is it function notation? Or part of set notation? None of the mathematics courses I’ve taken at my college has used this notation, but I’ve begun to encounter it in some of the calculus & analysis textbooks I’ve looked at, and I see it used here and elsewhere on the web.
The other part of my question is, where can I learn more about the following notation ? It seems like notation like this should be covered in some course, but I haven’t encountered on yet which did cover it:
$$f : \mathbb \to \mathbb \quad \text \quad f : \mathbb \to \mathbb$$
I understand this is a form of function notation, but I wasn’t sure what to call it, and thus what would make a good google query. When I googled “function notation,” of course, the results I got back were about the familiar $y=f$ notation.
Symbols That Do Not Belong To Formulas

In this section, the symbols that are listed are used as some sorts of punctuation marks in mathematical reasoning, or as abbreviations of English phrases. They are generally not used inside a formula. Some were used in classical logic for indicating the logical dependence between sentences written in plain English. Except for the first two, they are normally not used in printed mathematical texts since, for readability, it is generally recommended to have at least one word between two formulas. However, they are still used on a black board for indicating relationships between formulas.
- ,
- Used for marking the end of a proof and separating it from the current text. The initialismQ.E.D. or QED is often used for the same purpose, either in its upper-case form or in lower case.
- Bourbaki dangerous bend symbol: Sometimes used in the margin to forewarn readers against serious errors, where they risk falling, or to mark a passage that is tricky on a first reading because of an especially subtle argument.
- Abbreviation of “therefore”. Placed between two assertions, it means that the first one implies the second one. For example: “All humans are mortal, and Socrates is a human. Socrates is mortal.”
- Abbreviation of “because” or “since”. Placed between two assertions, it means that the first one is implied by the second one. For example: “11 is prime it has no positive integer factors other than itself and one.”
You May Like: How To Calculate Frequency Physics
Using The Vertical Line Test
As we have seen in some examples above, we can represent a function using a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value \ and the output \, and we say \ is a function of \, or \\) when the function is named \. The graph of the function is the set of all points \\) in the plane that satisfies the equation \\). If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. For example, the black dots on the graph in Figure \ tell us that \=2\) and \=1\). However, the set of all points \\) satisfying \\) is a curve. The curve shown includes \\) and \\) because the curve passes through those points
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. See Figure \.
Howto: Given a graph, use the vertical line test to determine if the graph represents a function
Example \: Applying the Vertical Line Test
What Is A Function On A Graph
A function f can be represented on a graph by knowing the values of x. As we know, y = f, so if start putting the values of x we can get the related value for y. Hence, we can plot a graph using x and y values in a coordinate plane. Let us see an example:
Suppose, y = x + 3
- when x = 0, y = 3
- when x = -2, y = -2 + 3 = 1
- when x = -1, y = -1 + 3 = 2
- when x = 1, y = 1 + 3 = 4
- when x = 2, y = 2 + 3 = 5
Thus, with the help of these values, we can plot the graph for function x + 3.
Recommended Reading: How Do Noise Cancelling Headphones Work Physics
Evaluation Of Functions In Algebraic Forms
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function \=53x^2\) can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
How To: Given the formula for a function, evaluate.
Given the formula for a function, evaluate.
What Is Function Notation
Function notation is a method of writing algebraic variables as functions of other variables. Most often, functions are portrayed as a set of x/y coordinates, with the vertical y-axis serving as a function of x. For example, writing “f = 3x” is the same as writing “y = 3x.”
Writing functional notation as “y = f” means that the value of variable y depends on the value of x. In the simple function “f = x + 3”, y intercepts the y-axis at point on the graph, because x is 0 and y is 3. From there, the line is a one-to-one function, with y and x increasing at the same rate. There are also compound functions that are useful in problems requiring more than one set of data. For example, “g)” means the initial function f is taken, then treated as the original x-value with a new line created on the graph.
Domain and range are two other concepts to understand. Domain refers to the set of independent variables for which a function applies. Range refers to the dependent variable, most often y. When writing domain and range, students use curly brackets and write the numbers from least to most, separating them with a comma.
You May Like: How To Teach 4th Grade Math
Determining Whether A Function Is One
Some functions have a given output value that corresponds to two or more input values. For example, in the stock chart shown in the Figure at the beginning of this chapter, the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in Table \.
| Letter Grade | |
|---|---|
| D | 1.0 |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, lets look again at the two simple functions sketched in Figures \ and \. The function in part shows a relationship that is not a one-to-one function because inputs \ and \ both give output \. The function in part shows a relationship that is a one-to-one function because each input is associated with a single output.
One-to-One Functions
A one-to-one function is a function in which each output value corresponds to exactly one input value.
Example \: Determining Whether a Relationship Is a One-to-One Function
Is the area of a circle a function of its radius? If yes, is the function one-to-one?
Solving And Evaluating Functions
When we work with functions, there are two typical things we do: evaluate and solve. ;Evaluating a function is what we do when we know an input, and use the function to determine the corresponding output. ;Evaluating will always produce one result, since each input of a function corresponds to exactly one output.
Solving equations involving a function is what we do when we know an output, and use the function to determine the inputs that would produce that output. ;Solving a function could produce more than one solution, since different inputs can produce the same output.
Example 7.1 G: Calculating Input and Output
Using the table shown, where
| 1 |
Solution:
Looking at the three graphs above, the first two define a function , since for each input value along the horizontal axis there is exactly one output value corresponding, determined by the -value of the graph. ;The 3rd graph does not define a function since some input values, such as , correspond with more than one output value.
You May Like: How To Find Biological Grandparents Uk
Fitting Lines With Technology
While eyeballing a line works reasonably well, there are statistical techniques for fitting a line to data that minimize the differences between the line and data values. This technique is called least-square regression, and can be computed by many graphing calculators, spreadsheet software like Excel or Google Docs, statistical software, and many web-based calculators.
Example 7.7D
Find the least-squares regression line using the cricket chirp data from above.
Using the cricket chirp data from earlier, with technology we obtain the equation:
Notice that this line is quite similar to the equation we eyeballed, but should fit the data better. Notice also that using this equation would change our prediction for the temperature when hearing 30 chirps in 15 seconds from 66 degrees to:
degrees.
Most calculators and computer software will also provide you with the correlation coefficient, a measure of how closely the line fits the data.
Functions And Function Notation
- Publisher: OpenStax CNX
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Read Also: What Is The Formula Of Volume In Physics
Finding Input And Output Values Of A Function
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the functions formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Graphs Of Linear Functions
When we are working with a new function, it is useful to know as much as we can about the function: its graph, where the function is zero, and any other special behaviours of the function.
When graphing a linear function, there are two basic ways to graph it:
- Using the initial value and rate of change
Example 7.5A
These evaluations tell us that the points , , and lie on the graph of the line. Plotting these points and drawing a line through them gives us the graph.
When using the initial value and rate of change to graph, we need to consider the graphical interpretation of these values. Remember the initial value of the function is the output when the input is zero, so in the equation , the graph includes the point . On the graph, this is the vertical intercept the point where the graph crosses the vertical axis.
For the rate of change, it is helpful to recall that we calculated this value as
From a graph of a line, this tells us that if we divide the vertical difference, or rise, of the function outputs by the horizontal difference, or run, of the inputs, we will obtain the rate of change, also called slope of the line.
Notice that this ratio is the same regardless of which two points we use
You May Like: Geometry Segment Addition Postulate Worksheet
Function Notation Explanation & Examples
The concept of functions was developed in the seventeenth century when Rene Descartes used the idea to model mathematical relationships in his book Geometry. The term function was then introduced by Gottfried Wilhelm Leibniz fifty years later after publication of Geometry.
Later, Leonhard Euler formalized the usage of functions when he introduced the concept of function notation; y = f . It was until 1837 when Peter Dirichlet a German mathematician;gave the modern definition of a function.
Advantages Of Using Function Notation
- Since most functions are represented with various variables such as; a, f, g, h, k etc., we use f in order avoid confusion as to which function is being evaluated.
- Function notation allows to identify the independent variable with ease.
- Function notation also helps us to identify the element;of a function which has to be examined.
Consider a linear function y;= 3x;+ 7. To write such function in function notation, we simply replace the variable y with the phrase f to get;
f = 3x;+ 7. This function f = 3x;+ 7 is read as the value of;f;at;x;or as;f;of;x.
You May Like: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Evaluating At A Number
You evaluate “f;” in exactly the same way that you’ve always evaluated “y“. Namely, you take the number they give you for the input variable, you plug it in for the variable, and you simplify to get the answer. For instance:
-
Given f; = x2 + 2x 1, find f;.
To evaluate f; at x = 2, I’ll plug 2 in for every instance of x in the function’s rule:
f; = 2 +2 1
To keep things straight in my head , I’ve put parentheses around every instance of the argument 2 in the formula for f. Now I can simplify:
2 + 2 1
Then my answer is:
f; = 2
If you experience difficulties when working with negatives, try using parentheses as I did above. Doing so helps keep track of things like whether or not the exponent is on the “minus” sign. And it’s just generally a good habit to develop.
Affiliate
An important type of function is called a “piecewise” function, so called because, well, it’s in pieces. For instance, the following is a piecewise function:
As you can see, this function is split into two halves: the half that comes before x = 1, and the half that goes from x = 1 to infinity. Which half of the function you use depends on what the value of x is. Let’s examine this:
-
Given the function f; as defined above, evaluate the function at the following values: x;=;1, x;=;3, and x;=;1.
This function comes in pieces; hence, the name “piecewise” function. When I evaluate it at various x-values, I have to be careful to plug the argument into the correct piece of the function.
f; = 22 1
= 2 1
= 2 1 = 1