Independence Of Horizontal And Vertical Motions
Neglecting the curvature of the earth, horizontal and vertical motions of a projectile moving under gravity are independent of each other. Vertical displacement of a projectile is not affected by the horizontal component of the launch velocity, and, conversely, the horizontal displacement is unaffected by the vertical component. The notion dates at least as far back as Galileo.
When the curvature of the earth is taken into account, the independence of the two motion does not hold. For example, even a projectile fired in a horizontal direction may leave the surface of the spherical earth and indeed escape altogether.
The Flat Earth Approximation
In the flat earth scenario, where the earth is notionally a large flat surface with gravitational field at a right angle to the surface, the earth surface is vertical and any plane parallel to the earth surface is also vertical. Horizontal planes, e.g., walls, may be parallel to each other or they may intersect at a vertical line. Horizontal surfaces do not intersect. Furthermore, a plane cannot both be a horizontal plane at one place and a vertical plane somewhere else. This Euclidean Three Space is measured with Right Line Geometry also known as Surveying.
What Does Square Mean
Square refers to perfect corners. Corners should be at exactly 90 degrees, which means they consist of two perpendicular lines: one straight horizontal line and one straight vertical line. Perpendicular lines meet to create a right angle, which is what you should have at every corner.
To ensure that a corner is square, you can use a tool known as a steel square, carpenter square or framing square. This tool helps you measure and mark perfect 90-degree angles, also known as right angles.;
You May Like: Geometry Segment Addition Postulate Worksheet
What Is The Difference Between Vertical And Adjacent Angles
Identifying the difference between adjacent angles and vertical angles is an important skill to master in geometry. The best way to visualize the difference between these two types of angles is to imagine two straight lines intersecting each other to form a cross.
When a cross is formed, four angles are formed. We know how to identify the adjacent angles, because they have a common side and a common vertex. But how do we identify a vertical angle? Identifying a vertical angle is equally as easy as finding an adjacent angle. Similarly to adjacent angles, a set of vertical angles will share a vertex point. However, they do not need to share a common side.
When thinking about a cross, the vertical angles are the angles that are opposite each other. This is why they are sometimes called vertically opposite angles.
What Is A Vertical Angle
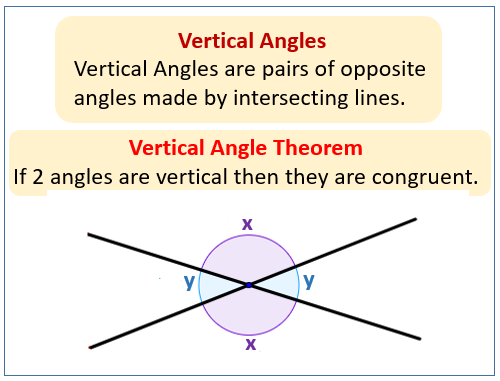
Vertical Angle Definition: In Mathematics, two;straight;lines;intersect;a point to;form;angles. The opposite pair of angles;after;the intersection of;two;straight;lines;are;known;as;vertically;opposite angles.;;
The vertical angle and its adjacent angles make supplementary angles, which means they are always 180 degrees.
Also Check: What Is The Molecular Geometry Of Ccl4
Vertically Opposite Angles Faqs
The frequently asked questions on vertical angles are given below:
| Q. Do all vertical angles equal 180? A. When two lines intersect at a point, two pair of vertical angles are created. Both pairs forms full angle that is 360 degree. Also, each pair of vertical angles are equal. Now, an angle from each pair of vertical angles are adjacent angle so they are supplementary and add up to 180 degree. |
| Q. Are vertical angles equal to each other?A. Yes, vertically angles or vertically opposite angles are always equal. |
| Q. Do vertical angles share a vertex? A. Yes, Vertical angles are always seen in pairs and they share a common vertex. |
What Did We Learn
Read Also: How To Login To Imagine Math
Vertical Angles: Theorem And Proof
Theorem: In a pair of intersecting lines the vertically opposite angles are equal.
Proof: Consider two lines \ and \ which intersect each other at \. The two pairs of vertical angles are:
i) AOD and COB
ii) AOC and BOD
It can be seen that ray \ stands on the line \ and according to Linear Pair Axiom, if a ray stands on a line, then the adjacent angles form a linear pair of angles.
Therefore, AOD + AOC = 180°
Similarly, \ stands on the line \.
Therefore, AOC + BOC = 180°
From and ,
Thus, the pair of opposite angles are equal.
Hence, proved.
Consider the figure given below to understand this concept.
In the given figure AOC = BOD and COB = AOD
BOD = 105° and AOD = 75°
To explore more, download BYJUS-The Learning App.
Properties Of Vertical Lines
- The equation of a vertical line in the graph, which is parallel to y-axis is x = a.
- The slope of a vertical line is infinity or undefined as it has no y-intercept and the denominator in the slope formula is zero.
- To check whether the relation is a function in maths, we use a vertical line. It would be a function if all vertical lines intersect it minimum once. This is also called a vertical line test. A graph will be considered as a function if it has only one output y for each input x. Therefore, a vertical line cannot be a function.
You May Like: What Is Figure Ground Perception Psychology
Solid Vertical Bar Vs Broken Bar
Many early video terminals and dot-matrix printers rendered the vertical bar character as the allographbroken bar¦. This may have been to distinguish the character from the lower-case ‘L’ and the upper-case ‘I’ on these limited-resolution devices, and to make a vertical line of them look more like a horizontal line of dashes. It was also part of the ASCII standard.
It may be desirable to employ distinctive styling to facilitate their use for specific purposes as, for example, to stylize the graphics in code positions 2/1 and 5/14 to those frequently associated with logical OR and logical NOT respectively.
X3.2 document X3.2/475
The original vertical bar encoded at 0x7C in the original May 12, 1966 draft was then broken as ¦, so it could not be confused with the unbroken logical OR. In the 1967 revision of ASCII, along with the equivalent ISO 464 code published the same year, the code point was defined to be a broken vertical bar, and the exclamation mark character was allowed to be rendered as a solid vertical bar. However, the 1977 revision undid the changes made in the 1967 revision, enforcing that the circumflex could no longer be stylised as a logical NOT symbol, the exclamation mark likewise no longer allowing stylisation as a vertical bar, and defining the code point originally set to the broken bar as a solid vertical bar instead; the same changes were also reverted in ISO 646-1973 published four years prior.
What Does True Mean
In construction, true is about everything being lined up correctly. Your lines should be perfectly vertical and horizontal , and your corners should be exactly 90 degrees .;
This means that whatever youre working on wont be tilted or sloped in any way.;
Every element of your orientation must be exact. Nothing should lean in any direction. If just one corner or one line of what youre building isnt straight, then what youre doing wont be true.
MT Copeland offers video-based online classes that give you a foundation in construction fundamentals with real-world applications. Classes include professionally produced videos taught by practicing craftspeople, and supplementary downloads like quizzes, blueprints, and other materials to help you master the skills.
Read Also: Fsa Algebra 1 Eoc Review Functions And Modeling Answer Key
When To Use The Theorem
If we are solving a geometry problem that has intersecting lines and we are given one of the angles, we can find the other three angles by using the vertical angles theorem. This is extremely useful for intersecting shapes and other angle-based problems. It works for triangles, rectangles, etc. It is the basis of the relationship between internal and external angles of shapes.
The Vertical Angles Theorem
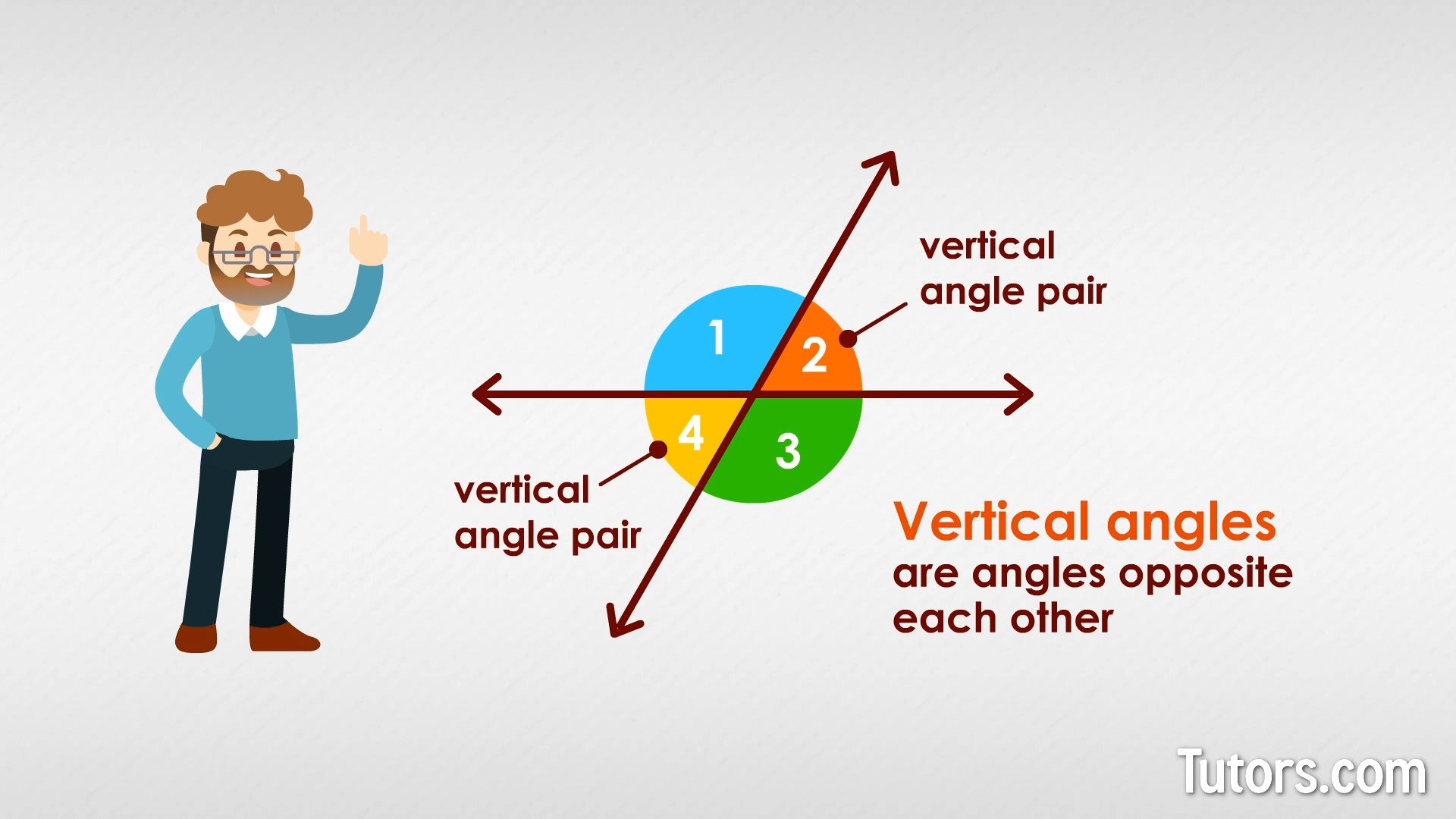
The vertical angles theorem tells us that angles opposite each other where two lines cross are congruent .In the image below, and are vertical and equal angles.
; ; ; ; ; A pair of vertical angles.
The vertical in vertical angles should not be confused with lines or angles being oriented up and down, as the word vertical implies. In this context, vertical means that the two angles are opposite each other about a shared apex.
Another name for vertical angles is vertically opposite angles. This name is very intuitive because it describes that the angles are opposite each other where two lines cross.
Read Also: How Many Questions Can You Miss On The Ged Math Test To Pass
Are Adjacent Angles Equal To 180
This is TRUE in some cases! Supplementary adjacent angles always add up to 180. This is because the two angles sit next to each other on a straight line and all angles on a straight line add up to 180.
However, if the adjacent angles are not linear pairs and another angle is in the mix, the two adjacent angles will not add up to 180.
Basic Mathematical Symbols With Name Meaning And Examples
The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.
| Symbol |
|---|
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Vertical Bar Sign In Discrete Mathematics
I am little bit confused about the sign ” | “. Some people call it the division sign and some call it “such that”. In computer programming, it’s known as pipe.
| => Such that sign| => Division sign| => Pipe sign
- 1$\begingroup$It has all three meanings, depending on context. In the second one, $a|b$ is often read verbally as “$a$ divides $b$”.$\endgroup$;coffeemathNov 27 ’14 at 12:52
- $\begingroup$LaTeX also offers a number of ways to evoke such a symbol. You can just put “|” inside MathJax delimiters, or use \mid or \vert, etc. See this Q at TeX.SE for details of what differences there are. The vertical stroke is also used as a delimiter in absolute values and in norms.$\endgroup$Nov 27 ’14 at 17:28
- 1
The sign $|$ has a few uses in mathematics
$$\text\$$
Here it the sign means “such that”, the colon also means “such that” in this context
Note that in this case it is written \mid in LaTeX, and not with the symbol |.
$$a\mid b$$
In this case the $\mid$ sign means that $a$ divides $b$, or that $\frac ba$ is an integer
Note that in this case it is written \mid in LaTeX, and not with the symbol |.
$$|x|$$
Here it means the absolute value of $x$, ie. $|x|=\left\x\quad&\textx\ge0\\-x&\textx<0\end\right.$
In this case it is written with just the | symbol. Note that sometimes you need to put around the contents to get the correct spacing, ie.
- |-2| gives $|-2|$
- || gives $||$
$ ls -l | grep "Aug"
Note that this last one isn’t really mathematics but I included it as you mentioned it.
Can Adjacent Angles Be Linear Pairs
YES! Adjacent angles can be linear pairs. As linear pairs share both a common side and a common vertex, they can be considered adjacent angles. However, not all adjacent angles are linear pairs.
This was a quick run through of adjacent angles to help you get to grips with this integral part of the geometry syllabus. However, theres always more that you can do to ensure you achieve the grade you want.
You May Like: Lesson 9.5 Geometry Answers
What Is A Spirit Or Bubble Level
A spirit levelsometimes known as a bubble level, carpenter level, or a torpedo level is a tool that uses gravity to measure if something is level.;;
These levels have a vial of liquid with an air bubble inside that runs parallel to the body of the tool. When the tool is level with the earth, the bubble is exactly in the middle of the vial, often marked with a line. If the tool is sloped or slanted in one direction, the bubble floats to the higher side.;
How To Use The Theorem
There are four angles where two lines cross . These four angles are labeled as A, B, C, and D in the image below. Congruent angles are marked with a like number of dashes as shown in the image below.
; ; ; ; ;Two pairs of vertical angles.
These four angles are make the two pairs of vertical angles. A = B and C = D. Because of what the vertical angles theorem tells us, we only need to know the value of one of these angles to determine all the others. The sum of angles around the crossing of two lines is always 360°.
The rules of geometry tell us that A + B + C + D = 360°. With simple arithmetic, we can find the other three angles from only knowing one angle. This is what makes the vertical angles theorem so powerful.
You May Like: Write The Segment Addition Postulate For The Points Described
Angles And Parallel Lines
When two lines intersect they form two pairs of opposite angles, A + C and B + D. Another word for opposite angles are vertical angles.
Vertical angles are always congruent, which means that they are equal.
Adjacent angles are angles that come out of the same vertex. Adjacent angles share a common ray and do not overlap.
The size of the angle xzy in the picture above is the sum of the angles A and B.
Two angles are said to be complementary when the sum of the two angles is 90°.
Two angles are said to be supplementary when the sum of the two angles is 180°.
If we have two parallel lines and have a third line that crosses them as in the ficture below – the crossing line is called a transversal
When a transversal intersects with two parallel lines eight angles are produced.
The eight angles will together form four pairs of corresponding angles. Angles 1 and 5 constitutes one of the pairs. Corresponding angles are congruent. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs e.g. 3 + 7, 4 + 8 and 2 + 6.
Angles that are in the area between the parallel lines like angle 2 and 8 above are called interior angles whereas the angles that are on the outside of the two parallel lines like 1 and 6 are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. 1 + 8.
Example
6 and 8 are vertical angles and are thus congruent which means angle 8 is also 65°.
The Plumb Line And Spirit Level
In physics, engineering and construction, the direction designated as vertical is usually that along which a plumb-bob hangs. Alternatively, a spirit level that exploits the buoyancy of an air bubble and its tendency to go vertically upwards may be used to test for horizontality. A water level device may also be used to establish horizontality.
Modern rotary laser levels that can level themselves automatically are robust sophisticated instruments and work on the same fundamental principle.
You May Like: Fsa Algebra 1 Eoc Review Functions And Modeling-answer Key
But Here It Has More To Do With The Word Vertex
What does vertical angles mean in geometry. They are also called vertically opposite angles. The angles opposite each other when two lines cross. Technically these two lines need to be on the same plane vertical angles are congruent in other words they have the same angle measuremnt or size as the diagram below shows.
A and b are vertical angles. Vertical angles are the angles opposite each other when two lines cross vertical in this case means they share the same vertex corner point not the usual meaning of up down. Vertical angles are a pair of non adjacent angles formed when two lines intersect.
Vertical angles are the angles that are opposite each other when two straight lines intersect. We see intersecting lines all the time in our real world. In this example a and b are vertical angles.
Vertical has come to mean upright or the opposite of horizontal. Here we see two vapor trails that intersect. They are always equal.
Try moving the points below.
Pin By Christiana Emory On Georgia Standards Math Quotes Middle School Math Math Geometry
Geometry Angles Frayer Model Vocabulary Vocabulary They Will Like And Use Geometry Angles Vertical Angles Vocabulary
Vertical Angles Definition Illustrated Examples And An Vertical Angles Angles Vertical
Vertically Opposite Angles And Around A Point Angles Math Formulas Opposites
Angles Relationships Complementary Adjacent Supplementary Vertical Congruent Math Anchor Charts Math Methods Teaching Math
Pin On Math Geometry
English Books Relating To Vertical Angles
vertical anglesvertical anglesVertical angles2011vertical angles1999vertical anglesVertical anglesvertical anglesvertical angles2012vertical anglesvertical anglesvertical angles2009Vertical anglesVertical angles2010vertical anglesVertical anglesverticalanglesvertical anglesVertical angles2008Vertical Anglesvertical anglesvertical anglesverticalanglesvertical anglesvertical anglesVertical2013
Recommended Reading: What Does Abiotic Mean