Elastic Force And The Factors Affecting It
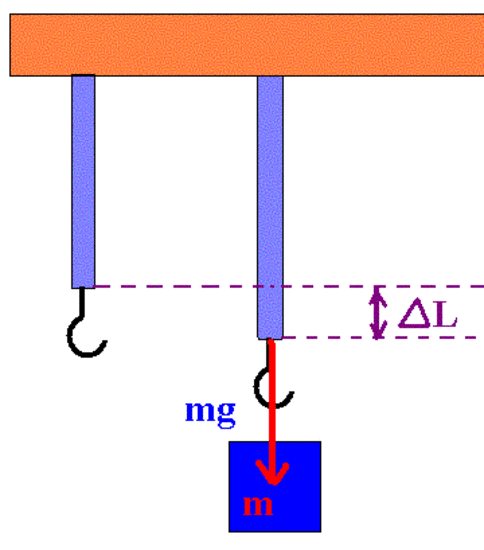
Suppose you have a perfectly elastic spring hanged in the vertical position as shown in the figure.
The original length of the spring is denoted by L0. If we hook an object of mass m on it, as shown in the figure below, the final length of the stretched spring becomes L.
We denote by x the difference between the actual position L and the original position L0 of the spring. It represents the linear deformation of the spring. Therefore, we have
Look at the figure below.
Figure 2. An elastic spring before and after hanging an object on it
Even during the compression, we use the same reasoning as well. The only difference is that in compression, the linear deformation x is negative because L < L0. Therefore, we say the linear deformation x is a vector quantity as it involves direction.
Since the object m is in equilibrium, it is clear that there are two equal and opposite forces acting on it. One is the gravitational force which acts downwards as it tries to send the object on the Earth surface, while the other is the resistive force of the spring which acts upwards as the spring tries to resist to any deformation caused by external factors . This resistive force is known as Elastic Force, Fe as it tries to restore the spring’s original length .
Since there is equilibrium, the resultant force acting on the object m is zero. Therefore, we have
The restoring force, also known as the Elastic Force is in the opposite direction to the deformation x. Its equation is
What Are The Applications Of The Elastic Collision
If you wish to learn more physics concepts with the help of interactive video lessons, download BYJUS The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Forces In Quantum Mechanics
The notion “force” keeps its meaning in quantum mechanics, though one is now dealing with operators instead of classical variables and though the physics is now described by the Schrödinger equation instead of Newtonian equations. This has the consequence that the results of a measurement are now sometimes “quantized”, i.e. they appear in discrete portions. This is, of course, difficult to imagine in the context of “forces”. However, the potentials V or fields, from which the forces generally can be derived, are treated similarly to classical position variables, i.e., V }} .
This becomes different only in the framework of quantum field theory, where these fields are also quantized.
Thus the notion “force” loses already part of its meaning.
The utility of Feynman diagrams is that other types of physical phenomena that are part of the general picture of fundamental interactions but are conceptually separate from forces can also be described using the same rules. For example, a Feynman diagram can describe in succinct detail how a neutron into an electron, proton, and neutrino, an interaction mediated by the same gauge boson that is responsible for the weak nuclear force.
The four fundamental forces of nature
| Property/Interaction |
|---|
, is the unit vector directed outward from the center of the Earth.
- E
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Experiment To Measure Hookes Law
| Scale reading |
| 500 |
| 600 |
The result will show that the extension of the load is directly proportional to the load added. Plotting a graph of extension against mass, a straight line graph that pass through the origin is obtained.
Development Of The Concept
Philosophers in antiquity used the concept of force in the study of stationary andmoving objects and simple machines, but thinkers such as Aristotle and Archimedes retained fundamental errors in understanding force. In part this was due to an incomplete understanding of the sometimes non-obvious force of friction, and a consequently inadequate view of the nature of natural motion. A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Galileo Galilei and Sir Isaac Newton. With his mathematical insight, Sir Isaac Newton formulated laws of motion that were not improved for nearly three hundred years. By the early 20th century, Einstein developed a theory of relativity that correctly predicted the action of forces on objects with increasing momenta near the speed of light, and also provided insight into the forces produced by gravitation and inertia.
Aristotelian physics began facing criticism in medieval science, first by John Philoponus in the 6th century.
In the early 17th century, before Newton’s Principia, the term “force” was applied to many physical and non-physical phenomena, e.g., for an acceleration of a point. The product of a point mass and the square of its velocity was named vis viva by Leibniz. The modern concept of force corresponds to the Newton’s vis motrix .
Don’t Miss: What Classes Do 11th Graders Take
Examples Of Elasticity In Physics
The elasticity of materials is a property that we test daily. Some examples are:
- Springs The springs that are under certain buttons, or that push the bread from the toaster up when it is ready, operate on the basis of elastic tension: they are compressed and accumulate potential energy, then they are released and regain their shape by throwing the bread up. toasted.
- Buttons. The buttons on the TV remote control operate thanks to the elasticity of the material that compose them, since they can be compressed under the force of our fingers, activating the circuit underneath, and then recovering their initial position , ready to be pressed again.
- The gum. The resin from which the gum or chewing gum is made is extremely elastic, to the point that we can compress it between the teeth or expand it by filling it with air and making a bomb, assuming that it will retain its more or less original shape.
- The tires. Of an airplane, a car, a motorcycle, they operate based on the elasticity of rubber, which once inflated with air, can withstand the enormous weight of the complete vehicle and deform slightly, but without losing its shape memory, so it exerts resistance and keeps the vehicle suspended.
Physics Tutorial: Types Of Forces Iii
In this Physics tutorial, you will learn:
- What are elastic objects?
- How to determine whether an object is elastic or not?
- What happens when an object is not elastic?
- What are the factors affecting the elasticity of objects?
- Where does the elastic force depend on?
- How to represent graphically a situation involving the elastic behaviour of matter?
- What is limit of elasticity and breaking point?
- What is tension?
- Where does the tension differ from elastic force?
Also Check: What Is The Molecular Geometry Of Ccl4
What Is Elasticity In Physics
When in physics we talk about elasticity, we refer to the property of certain materials to be deformed under an external force that acts on them and then recover their original shape when said force disappears. These types of behaviors are known as reversible deformations or shape memory.
Not all materials are elastic and those that break, fragment or remain deformed after the action of external force are simply not elastic at all.
The principles of elasticity are studied by the mechanics of deformable solids, according to the Theory of Elasticity, which explains how a solid deforms or moves in response to external forces that affect it.
Thus, when these deformable solids receive said external force, they deform and accumulate a quantity of elastic potential energy inside them and, therefore, also of internal energy.
Said energy, once the deforming force has been removed, will be the one that forces the solid to regain its shape and is transformed into kinetic energy, causing it to move or vibrate.
The magnitude of the external force and the coefficients of elasticity of the deformed object will be those that allow calculating the size of the deformation, the magnitude of the elastic response and the stress accumulated in the process.
See also: Inertia
What Is Elastic Limit
Elastic limit, maximum stress or force per unit area within a solid material that can arise before the onset of permanent deformation. When stresses up to the elastic limit are removed, the material resumes its original size and shape. Stresses beyond the elastic limit cause a material to yield or flow.
You May Like: Lewis Dot Structure Of Ccl4
What Is Hooke’s Law
by Matt Williams, Universe Today
The spring is a marvel of human engineering and creativity. For one, it comes in so many varieties the compression spring, the extension spring, the torsion spring, the coil spring, etc. all of which serve different and specific functions. These functions in turn allow for the creation of many man-made objects, most of which emerged as part of the Scientific Revolution during the late 17th and 18th centuries.
As an elastic object used to store mechanical energy, the applications for them are extensive, making possible such things as an automotive suspension systems, pendulum clocks, hand sheers, wind-up toys, watches, rat traps, digital micromirror devices, and of course, the Slinky.
Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play which together are known as Hooke’s Law.
This can be expressed mathematically as F= -kX, where F is the force applied to the spring ; X is the displacement of the spring, with a negative value demonstrating that the displacement of the spring once it is stretched; and k is the spring constant and details just how stiff it is.
There are also some great resources online, such as this lecture on Hooke’s Law that you can watch on academicearth.org. There is also a great explanation of elasticity on howstuffworks.com.
Elastic Force And Elastic Potential Energy Calculator
The Elastic Force and Elastic Potential Energy Calculator is provided in support of our Physics Tutorials on Kinematics and Work, Energy and Motion which explores Motion, the different types of energy, kinetic energy, gravitational potential energy, elastic potential energy. power and efficiency with practical working examples and formula. A list of the supporting Work and Energy Physics Tutorials is available at the bottom of this page. This calculator will calculate:
| Normal View |
| Initial length of the spring m |
| Final length of the spring m |
| Deformation m |
| Elastic Force N |
| Elastic Potential Energy J |
Note: If the question you are looking to answer provides the value of deformation x, please write two random values for the initial and final length of the spring that fit the description. For example, if the question says, “the spring is stretched by 20 cm”, you can insert the values 0.5 for L0 and 0.7 for L as x = L – L0 = 0.7 m – 0.5 m = 0.2 m = 20 cm.
Read Also: Why Am I Always Late Psychology
Is Gravity An Elastic Force
The universal law of Gravitation states that the force of gravity acts between all objects in the universe. compression and tension are two types of elastic forces. Compression is an elastic force that squeezes or pushes matter together and tension is an elastic forcce that stretches or pulls matter.
Applications Of Elastic Collision
- The collision time affects the amount of force that an object experiences during a collision. The greater the time over which the collision occurs, the smaller the force acting upon the object. Thus, to maximize the force experienced by an object during a collision, the collision time must be decreased.
- Likewise, to minimize the force, the collision time must be increased. There are several real-world applications of these phenomena. The airbags in automobiles increase the collapse time and minimize the effect of force on objects during a collision. Airbag accomplishes this by extending the time required to stop the momentum of the passenger and the driver.
Watch the video to learn about Coefficient-of-Restitution.
Don’t Miss: Geometry Segment Addition Postulate Worksheet
On The Definition Of Elastic Restoring Force In A Spring
How is the elastic restoring force defined exactly for a spring? We know by Hooke’s law that
$$F_\text = -kx$$
but what does $F_\text$ really mean? I thought up till now that it was the force the spring pulled with at both ends if you stretched it by a distance $x$. This definition worked pretty well until I encountered some problems when I was doing problems a little above my usual level.
I have stripped down the problem I encountered to its core :
Consider a spring attached to a wall in its relaxed. If we pull it with a force $F$, clearly the spring exerts a pulls with a force $F$. However, initially the spring is unstretched. The definition fails in this case.
What is the precise definition of a restoring force in a spring in the most general case?
The word ‘restoring’ is synonymous with ‘opposing’ in that it matches the applied force, but in the opposite direction. But more so ‘restoring’ implies that energy is being stored – potential energy – which can subsequently be retrieved. The potential energy is the integral of force over the path of deflection:
$$E_p=kx^2$$
The energy imparted by the pulling force is stored in the spring which is able to do work.
In it’s relaxed state one can arbitrarily assign ‘zero’ potential energy by defining ‘x’ as zero at that position. Any deflection relative to zero stores energy.
Another interpretation is the fact that springs tend to ‘restore’ position to the relaxed state once the net external forces are removed.
What Is Elastic Force In Science
Elastic Forceelasticforceforceelastic forceelastic force
An example of elastic force is bungee jumping.The elastic cord creates resistance and imposes a force when the cord is stretched far enough. The farther the elastic is stretched, the more force it exerts to return back to its original shape.
Also Know, what are two types of elastic forces? Matter is elastic if it returns to its original shape after it is squeezed or stretched; There are two types of elastic forces– compression and tension.
Also know, what is tension and elastic force?
Elastic force is the force that a body exerts on itself whenever it’s under elastic deformation. Tension is just any kind of force that’s normal to the surface and pulling out Elastic forces are an example of a tension, bit it’s internal.
What is the formula for elastic force?
Elastic potential energy is equal to the force times the distance of movement. Elastic potential energy = force x distance of displacement. Because the force is = spring constant x displacement, then the Elastic potential energy = spring constant x displacement squared.
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers
Basic Spring Elements And Stiffness
Springs are mechanical elements that generate elastic forces in translatory motion and elastic torques in rotary motion; these elastic reactions oppose the spring deformation and are proportional to the spring linear or angular deformation.
Figure;2.1 sketches one of the most common spring configurationsthe helical springwhich can be used for either axial deformation or torsion-generated deformation. The parameters defining the helical spring are the mean diameter D, the wire diameter d, the number of active turns N, and the material shear and Young’s moduli, G and E. For a general spring whose end points undergo the displacements x1 and x2 , the elastic force developed in the spring, fe, is proportional to the spring deformation, which is the difference between the two end point displacements. The elastic force is expressed in Table;2.1, where kt is the translatory spring stiffness.
Figure;2.1. Helical Spring With Symbols for Translatory and Rotary Motion.
Table;2.1. Elastic Force/Moment and Elastic Potential Energy for Translatory and Rotary Springs
| Translation |
|---|
| ) 2 |
Table;2.2. Basic Translatory Springs and Their Lumped-Parameter Stiffnesses
| Configuration |
|---|
This equation is particularly important because it ties together thermodynamic and molecular concepts.
TABLE II. Comparison of d ln r20/dT Deduced from Thermoelastic Measurements on a Network with Values from Viscosity Measurements on Isolated Chainsa
| 103d lnr20/dT |
|---|
J. G.Holierhoek, in, 2013
Formula Of Elasticity In Physics
When a force is applied to an elastic material, it deforms or compresses. For mechanics, the important thing is the amount of force applied per unit area, which we will call effort .
We will call the degree of stretching or compression of matter deformation and we will calculate it by dividing the length of movement of the solid by its initial length , that is: = L / L 0.
On the other hand, one of the main laws that governs the phenomenon of elasticity is the Hooke’s law. This law was formulated in the seventeenth century by physicist Robert Hooke when he studied a spring and realized that the force necessary to compress it was proportional to the variation in its elongation when applying said force.
This law is formulated as follows: F = k.x where F is the force, x the length of the compression or elongation, and k a constant of proportionality expressed in Newtons over meters .
Finally, the elastic potential energy associated with the elastic force it is represented by the formula: Ep = ½. k.x2.
Recommended Reading: Geometry Segment Addition Postulate Worksheet