Area And Perimeter Of A Parallelogram
The parallelogram has two sets of opposite sides that run parallel to one another. The shape is a quadrangle, so it has four sides: two sides of one length and two sides of another length .
To find out the perimeter of any parallelogram, use this simple formula:
- Perimeter = 2a + 2b
When you need to find the area of a parallelogram, you will need the height . This is the distance between two parallel sides. The base is also required and this is the length of one of the sides.
- Area = b x h
Keep in mind that the;b;in the area formula is not the same as the;b;in the perimeter formula. You can use any of the sideswhich were paired as;a;and;b;when calculating perimeterthough most often we use a side that is perpendicular to the height.;
The Surface Area And The Volume Of Pyramids Prisms Cylinders And Cones
The surface area is the area that describes the material that will be used to cover a geometric solid. When we determine the surface areas of a geometric solid we take the sum of the area for each geometric form within the solid.
The volume is a measure of how much a figure can hold and is measured in cubic units. The volume tells us something about the capacity of a figure.
A prism is a solid figure that has two parallel congruent sides that are called bases that are connected by the lateral faces that are parallelograms. There are both rectangular and triangular prisms.
To find the surface area of a prism we open the solid like a carton box and flatten it out to find all included geometric forms.
To find the volume of a prism we multiply the area of the base, called the base area B, by the height h.
$$V=B\cdot h$$
A cylinder is a tube and is composed of two parallel congruent circles and a rectangle which base is the circumference of the circle.
Example
The area of one circle is:
$$A=\pi r^$$
$$A=\pi \cdot 2^$$
$$A=\pi \cdot 4$$
The circumference of a circle:
$$C=\pi d$$
The area of the rectangle:
$$A=C\cdot h$$
The surface area of the whole cylinder:
$$A=75.6+12.6+12.6=100.8\, units^$$
To find the volume of a cylinder we multiply the base area and the height h.
$$V=\pi r^\cdot h$$
The volume of a pyramid is one third of the volume of a prism.
$$V=\frac\cdot B\cdot h$$
The surface area of a cone is thus the sum of the areas of the base and the lateral surface:
Example
Rectangular Solid Or Cuboids
A rectangular solid is also called a rectangular prism or a cuboid. In a rectangular solid,the length, width and height may be of different lengths.
The surface area of the above cuboid would be the sum of the area of all the surfaces which arerectangles.Total area of top and bottom surfaces is lw + lw = 2lw
Total area of front and back surfaces is lh + lh = 2lh
Total area of the two side surfaces is wh + wh = 2wh
Surface area of rectangular solid = 2lw + 2lh + 2wh = 2
Worksheets and More Examples on Rectangular Prisms:
How to find the surface area of a rectangular prism or cuboid?
Example:
Don’t Miss: How To Use Manipulatives In Math
Surface Area Of A Sphere
You can infer the formula for the surface area of a sphere by taking measurements of spheres and cylinders.;Here we show a sphere with a radius of 3 and a right cylinder with both a radius and a height of 3 and express;the area in terms of .
Now try a larger pair, expressing the surface area in decimal form.
Look at a third pair.
Is it a coincidence that a sphere and a cylinder whose radius and height are equal to the radius of the sphere;have the exact same surface area? Not at all! In fact, the ancient Greeks used a method that showed that;the following formula can be used to find the surface area of any sphere .
The Surface Area of a SphereAr
Surface Area And Volume Of A Pyramid
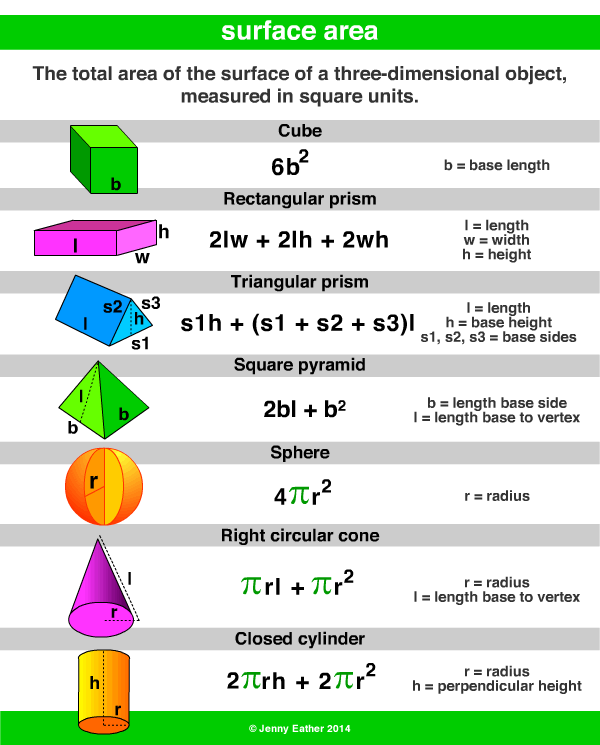
A pyramid with a square base and faces made of equilateral triangles is relatively easy to work with.
You will need to know the measurement for one length of the base . The height is the distance from the base to the center point of the pyramid. The side is the length of one face of the pyramid, from the base to the top point.
- Surface Area = 2bs + b2
- Volume = 1/3 b2h
Another way to calculate this is to use the perimeter and the area of the base shape. This can be used on a pyramid that has a rectangular rather than a square base.
- Surface Area = + A
- Volume = 1/3 Ah
Also Check: What Is The Molecular Geometry Of Ccl4
Shapes With Curved Surfaces
Although a little harder to visualize, shapes with curved surfaces have surface area too. The cylinder on the right can be thought of as two circles at each end and a strip wrapped around to form the body.
The two circles have an area of r2. The strip is a rectangle of width h, and a length equal to the circumference of each circle . So again we can determine the total surface area as the sum of the two circles and the rectangular strip.
See Surface area of a cylinder for an animated demonstration of this.
What Is The Definition Of Surface Area In Math
areasurfacesurface areaarea
An understanding of surface area is important to the chemist because chemical reactions occur between particles on the surface of the bulk of mass. The size of the surface area plays an important role in determining the rate of a chemical reaction. The larger the surface area, the faster the rate of reaction.
Beside above, how do you find the surface area? How to find the surface area of Rectangular Prisms:
Similarly, you may ask, what is surface area examples?
Surface Area Terms DefinedFor example, a sphere and a cube are three-dimensional, but a circle and a square are not. A cube is a prism, but a sphere is not. A prism has a pair of congruent sides, called bases, like the cube, triangular prism and the rectangular prism.
What is the surface area of a shape?
Surface–area. If a solid is composed of flat surfaces, such as the cube on the right, the surface area is simply the sum of the areas of the flat surfaces . So, for example, if a each edge of a cube has a length s, the area of one face is s2 since it is a square.
Don’t Miss: Structure Of Ccl4
Surface Area Of A Prism Using Nets
The prisms above are right prisms. In a right prism, the lateral sides are perpendicular to the bases of;prism. Compare a right prism to an oblique prism, in which sides and bases are not perpendicular.
Two postulates that apply to area are the Area Congruence Postulate and the Area Addition Postulate.
Area Congruence Postulate:Area Addition Postulate:
You can use a net and the Area Addition Postulate to find the surface area of a right prism.
From the net, you can see that that the surface area of the entire prism equals the sum of the figures that;make up the net:
Total surface area = area A + area B + area C + area D + area E + area F
Using the formula for the area of a rectangle, you can see that the area of rectangle A is:
A = l · wA = 10;· 5 = 50;square units
Similarly, the areas of the other rectangles are inserted back into the equation above.
Total surface area = area A + area B + area C + area D + area E + area FTotal surface area = + + + + + Total surface area = 50 + 30 + 50 + 30 + 15 + 15Total surface area = ;190 square units
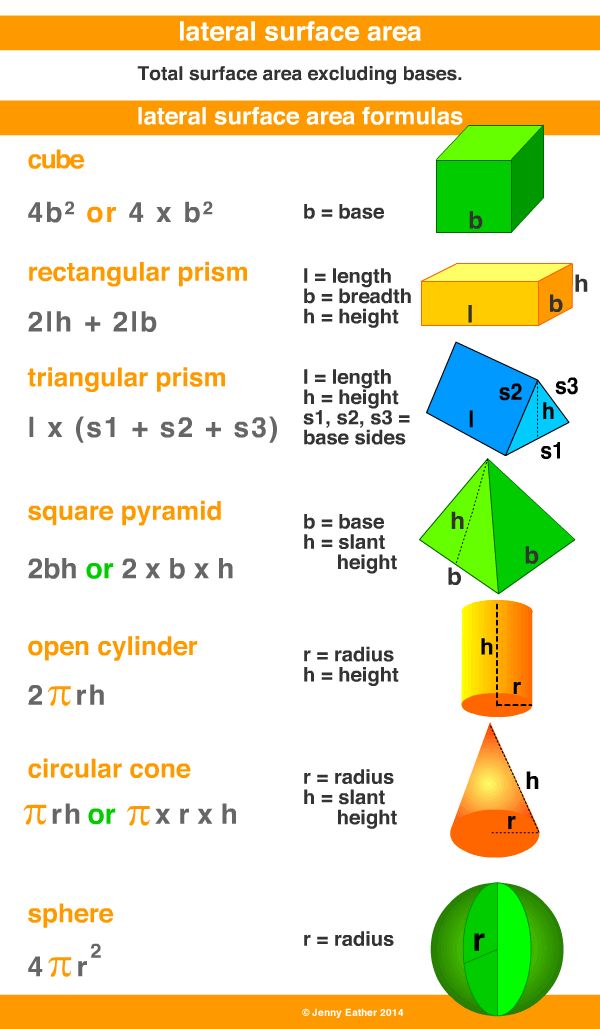
When Would You Use A Curved Surface Area
The curved surface area refers to the area of only the curved part of a 3D figure. In general, the lateral surface area and curved surface areas are the same in meaning. For example: In cuboid we use lateral surface area whereas in case of cylinder its curved surface area when you exclude its top and base surfaces.
Don’t Miss: Michael Jackson Kids Biological Parents
What Is Difference Between Total Surface Area And Lateral Surface Area
The total surface area of a solid is the sum of the areas of all of the faces or surfaces that enclose the solid. The faces include the tops and bottoms and the remaining surfaces. The lateral surface area of a solid is the surface area of the solid without the bases. Imagine a soup can.
Surface Area And Volume Of A Prism
When you switch from a pyramid to an isosceles triangular prism, you must also factor in the length of the shape. Remember the abbreviations for base , height , and side because they are needed for these calculations.
- Surface Area = bh + 2ls + lb
- Volume = 1/2 l
Yet, a prism can be any stack of shapes. If you have to determine the area or volume of an odd prism, you can rely on the area and the perimeter of the base shape. Many times, this formula will use the height of the prism, or depth , rather than the length , though you may see either abbreviation.
- Surface Area = 2A + Pd
Don’t Miss: What Are The Major Specialties In Psychology
Be Careful Units Count Use The Same Units For All Measurements Examples
| Surface Area of a Cube = 6 a2 |
In words, the surface area of a cube is the area of the six squares that cover it. The area of one of them is a*a, or a 2 . Since these are all the same, you can multiply one of them by six, so the surface area of a cube is 6 times one of the sides squared.
| Surface Area of a Rectangular Prism = 2ab + 2bc + 2ac |
In words, the surface area of a rectangular prism is the area of the six rectangles that cover it. But we don’t have to figure out all six because we know that the top and bottom are the same, the front and back are the same, and the left and right sides are the same.
The area of the top and bottom = a*c. Since there are two of them, you get 2ac. The front and back have side lengths of b and c. The area of one of them is b*c, and there are two of them, so the surface area of those two is 2bc. The left and right side have side lengths of a and b, so the surface area of one of them is a*b. Again, there are two of them, so their combined surface area is 2ab.
| Surface Area of Any Prism |
Surface Area = Lateral area + Area of two ends
= * L
Surface Area = * L+ 2*
| Surface Area of a Sphere = 4 pi r 2 |
| Surface Area of a Cylinder = 2 pi r 2 + 2 pi r h |
Surface Area = Areas of top and bottom +Area of the side
Surface Area = 2 + * height
Surface Area = 2 + * h
You can find the area of the top . That’s the formula for area of a circle . Since there is both a top and a bottom, that gets multiplied by two.
Surface Area = 2 + * h
= 6*
Surface Area Of Sphere
A sphere is a three-dimensional solid object which has a round;structure, like a;circle.;The area covered by the outer surface of the sphere is known as the surface;area;of a sphere.;The surface area of a sphere is the total area of the faces surrounding it. The surface area of a sphere is given in square units.
The surface area of a sphere is equal to the;lateral;surface area of a cylinder. Hence, the relation between the surface area;of a sphere;and lateral surface area of a cylinder is given as:Surface Area of Sphere;= Lateral Surface Area of Cylinder The surface area of Sphere =;2rhIf;a diameter of sphere = 2rThen the surface area of sphere is;2rh =;2r = 4r2;square units.
Read Also: Geometry Segment Addition Postulate Worksheet
Area And Perimeter Of A Rectangle
The rectangle is also a quadrangle. Unlike the parallelogram,;the interior angles are always equal to 90 degrees. Also, the sides opposite one another will always measure the same length.
To use the formulas for perimeter and area, you will need to measure the rectangle’s length and its width .
- Perimeter = 2h + 2w
What Is The Difference Between Total Surface Area And Volume
Surface area is the sum of the areas of all the faces of the solid figure. Finding surface area of solid figure is like finding how much wrapping paper that is required to cover the solid; it is the area of the outside faces of a box. Volume is the amount of space inside of the solid figure.
Also Check: What Classes Do 11th Graders Take
Surface Area Of A Cylinder Using A Formula
You have seen how to use nets to find the total surface area of a cylinder. The postulate can be broken;down to create a general formula for all right cylinders.
A = 2B +;L
Notice that the base, B, of any cylinder is:;B =;r2
The lateral area, L, for any cylinder is:
L=\text\cdot\text\\L=\text\cdot\text\\L=2\pi\cdot\\
Putting the two equations together we get:
Factoring out a from the equation gives:
The Surface Area of a Right Cylinder: A right cylinder with radius r;and height h;can;be expressed as:
A = 2r2 + 2rh
A sphere is a three-dimensional figure that has the shape of a ball.
Spheres can be characterized in three ways.
- A sphere is the set of all points that lie a fixed distance r;from a single center point O.
- A sphere is the surface that results when a circle is rotated about any of its diameters.
Surface Area Of Solid Cylinder
A cylinder is a solid that has two parallel faces which are congruent circles. These facesform the bases of the cylinder. The cylinder has one curved surface.
The height of the cylinder is the perpendicular distance between the two bases.
The net of a solid cylinder consists of 2 circles and one rectangle. The curved surfaceopens up to form a rectangle.
Surface area = 2 × area of circle + area of rectangle
Surface Area = 2r2 + 2rh = 2r
Worksheets and More Examples:
How to find the surface area of a cylinder?How to obtain the total surface of a cylinder by looking at the net of the cylinder?
Example:
You May Like: What Classes Do 11th Graders Take
Surface Area And Volume Of A Sphere
A three-dimensional circle is known as a sphere. In order to calculate either the surface area or the volume of a sphere, you need to know the radius . The radius is the distance from the center of the sphere to the edge and it is always the same, no matter which points on the sphere’s edge you measure from.
Once you have the radius, the formulas are rather simple to remember. Just as with the circumference of the circle, you will need to use pi . Generally, you can round this infinite number to 3.14 or 3.14159 .
- Surface Area = 4r2
Surface Area Of A Cylinder Using Nets
You can deconstruct a cylinder into a net.
The area of each base is given by the area of a circle:
A=\pi^2\\A=\pi^2\\A=25\pi\\A\approx=78.5\\
The area of the rectangular lateral area L is given by the product of a width and height. The height is given;as 24. You can see that the width of the area is equal to the circumference of the circular base.
To find the width, imagine taking a can-like cylinder apart with a scissors. When you cut the lateral area,;you see that it is equal to the circumference of the cans top. The circumference of a circle is given by;C = 2r,;the lateral area, L, is
L=2rh\\L=2\\L=240\pi\\L\approx=753.6\\
Now we can find the area of the entire cylinder using;A = + .
A=2+753.6\\A=904.32\\
You can see that the formula we used to find the total surface area can be used for any right cylinder.
Area of a Right Cylinder:hABLBL;
You May Like: Lewis Structure For Ccl4
Surface Area Formulas For Prisms
For every 3D solid, we can examine each face or surface and calculate its surface area. Then, adding all the individual surface areas, we can find the surface area of the entire solid.
Think of it as unfolding the 3D shape like a cardboard box. Lay out every face, measure each, and add them. This is what occurs with geometry nets.
Formulas work for all the prisms. The faces of prisms will be recognizable polygons, so let’s review the area formulas for the basic polygons:
Surface Area Of A Cylinder

To find out the surface area of a cylinder, you should have two values: the radius of a base and the height of the cylinder. The general equation is as usual – base area times height. In our case, a circle is a base.
- A = 2r² + 2rh
Where does this formula come from? You can write the equation for the surface area of a cylinder as:
- A = A + 2 * A
It’s easy to find a base area – we remember the well-known formula for the area of a circle: A = * r². But what’s the shape of the lateral surface area? Try to imagine that we “unfold” it. Do you recognize it? It’s a rectangle! One side length is a cylinder height and second one is the unfolded circle circumference.
- A = * r²
- A = h *
Read Also: How Does A Hydraulic Lift Work