Example : The Stretch Of A Long Cable
Suspension cables are used to carry gondolas at ski resorts. Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is\boldsymbol}.
Figure 4.
Strategy
The force is equal to the maximum tension, or\boldsymbol}.The cross-sectional area is\boldsymbol^2=2.46\times10^\textbf^2}.The equation\boldsymbol=\frac\fracL_0}can be used to find the change in length.
Solution
All quantities are known. Thus,
Discussion
This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.
Figure 5.
Stress Strain And Elastic Modulus
- Explain the concepts of stress and strain in describing elastic deformations of materials
- Describe the types of elastic deformation of objects and materials
A model of a rigid body is an idealized example of an object that does not deform under the actions of external forces. It is very useful when analyzing mechanical systemsand many physical objects are indeed rigid to a great extent. The extent to which an object can be perceived as rigid depends on the physical properties of the material from which it is made. For example, a ping-pong ball made of plastic is brittle, and a tennis ball made of rubber is elastic when acted upon by squashing forces. However, under other circumstances, both a ping-pong ball and a tennis ball may bounce well as rigid bodies. Similarly, someone who designs prosthetic limbs may be able to approximate the mechanics of human limbs by modeling them as rigid bodies however, the actual combination of bones and tissues is an elastic medium.
The SI unit of stress is the pascal . When one newton of force presses on a unit surface area of one meter squared, the resulting stress is one pascal:
In the British system of units, the unit of stress is psi, which stands for pound per square inch . Another unit that is often used for bulk stress is the atm . Conversion factors are
As we can see from dimensional analysis of this relation, the elastic modulus has the same physical unit as stress because strain is dimensionless.
What Is Thermal Stress In Physics
Stress caused due to the change in temperature
Thermal Stress Formula:
Thermal stress = \ = Y
where, = Coefficient of linear expansion of the material of the rod.When temperature of a gas enclosed in a vessel is changed, then the thermal stress produced is equal to change in pressure of the gas.
Thermal stress = p = K
where,K = Bulk modulus of elasticity = Coefficient of cubical expansion of the gas.
Elasticity:Elasticity defines a property of an object that has the ability to regain its original shape after being stretched or compressed. Learn about the deforming force applied on an elastic object and how the stress and strain works on an object. What is a Hookes law and how it is applicable for the concept of elasticity.
Read Also: The Founder Of Behaviorism Was:
Ratios Proportions And Angles
Dimensionless quantities are often obtained as of that are not dimensionless, but whose dimensions cancel out in the mathematical operation. Examples include calculating or . A more complex example of such a ratio is , a measure of physical deformation defined as a change in length divided by the initial length. Since both quantities have the dimension length, their ratio is dimensionless. Another set of examples is or often written using such as ppm , ppb , and ppt , or perhaps confusingly as ratios of two identical units ” rel=”nofollow”> mol/mol). For example, , which characterizes the concentration of in an , could be written as mL / 100 mL.
Other common proportions are percentages , and angle units such as , . In the is the ratio of the to the and is used to measure the in the .
It has been argued that quantities defined as ratios Q = A/B having equal dimensions in numerator and denominator are actually only unitless quantities and still have physical dimension defined as dim Q = dim A × dim B1.For example, may be defined as a ratio of volumes or as a ratio of masses both would be unitless quantities, but of different dimension.
D3 = Kok31e1 + Kok32e2 + Kok33e3
So you can see that even if E1 is the only non-zero value in the electric field, all the components of Di may be non-zero.
Rank of a Tensor
Tensors are referred to by their “rank” which is a description of the tensor’s dimension. A zero rank tensor is a scalar, a first rank tensor is a vector a one-dimensional array of numbers. A second rank tensor looks like a typical square matrix. Stress, strain, thermal conductivity, magnetic susceptibility and electrical permittivity are all second rank tensors. A third rank tensor would look like a three-dimensional matrix a cube of numbers. Piezoelectricity is described by a third rank tensor. A fourth rank tensor is a four-dimensional array of numbers. The elasticity of single crystals is described by a fourth rank tensor.
Tensor transformation
We can then express p1, p2,and p3 in terms of p1, p2, and p3:
You May Like: Finding Average Speed Physics
Strain: Definition Types Unit And Formula
Strain in Physics: A rigid body in Physics is a theoretical solid in which deformation is always zero no matter how much force we apply. Real solids are not perfectly rigid, and when we apply force on them, they undergo deformation. The amount of deformation produced depends upon the nature of the material and the stress developed within the solid. Stress is simply the internal force developed per unit area within the solid when an external force is applied.
As There Are Three Types
Tensile stress
When the deformation consists of a change in the length of the body, the strain is called tensile strain or longitudinal strain.
Consider the uniform metal wire of length L is subjected to a load F=mg, so that its length increases by l, then the final length of wire is L+l
Increase in length= L+l-L = l
The ratio of change in length per unit original length is called tensile strain.
Tensile strain = / = l/L
Volume strain
When the deformation consists of a change in volume of the body, the strain in it is called Volume strain.
Suppose that the cube of volume V is subjected to external load F, then the volume is shrinks by dV
Hence, change in volume= V-dV-V= -V
Negative sign indicates that the volume is decreased.
The ratio of change volume to original volume.
Volume Strain= / = dv/V
Shearing strain
When the deformation consists of a change in the shape of the body the strain in it is called shearing strain or shear.
Consider the cube of volume V is subjected to tangential force F so that the upper face of cube is displaced x or by angle as shown below,
The ratio of change in shape to the original shape.
Or Ratio of lateral displacement of layer to the distance of that layer from the fixed layer.
Shearing strain = /
Shearing strain = x/h
Shearing strain = tan
Don’t Miss: Who Are Paris Jackson’s Biological Parents
Sideways Stress: Shear Modulus
illustrates what is meant by a sideways stress or a shearing force. Here the deformation is called and it is perpendicular to , rather than parallel as with tension and compression. Shear deformation behaves similarly to tension and compression and can be described with similar equations. The expression for shear deformation is
where is the shear modulus ) and is the force applied perpendicular to and parallel to the cross-sectional area . Again, to keep the object from accelerating, there are actually two equal and opposite forces applied across opposite faces, as illustrated in . The equation is logicalfor example, it is easier to bend a long thin pencil than a short thick one, and both are more easily bent than similar steel rods .
Examination of the shear moduli in reveals some telling patterns. For example, shear moduli are less than Youngs moduli for most materials. Bone is a remarkable exception. Its shear modulus is not only greater than its Youngs modulus, but it is as large as that of steel. This is why bones are so rigid.
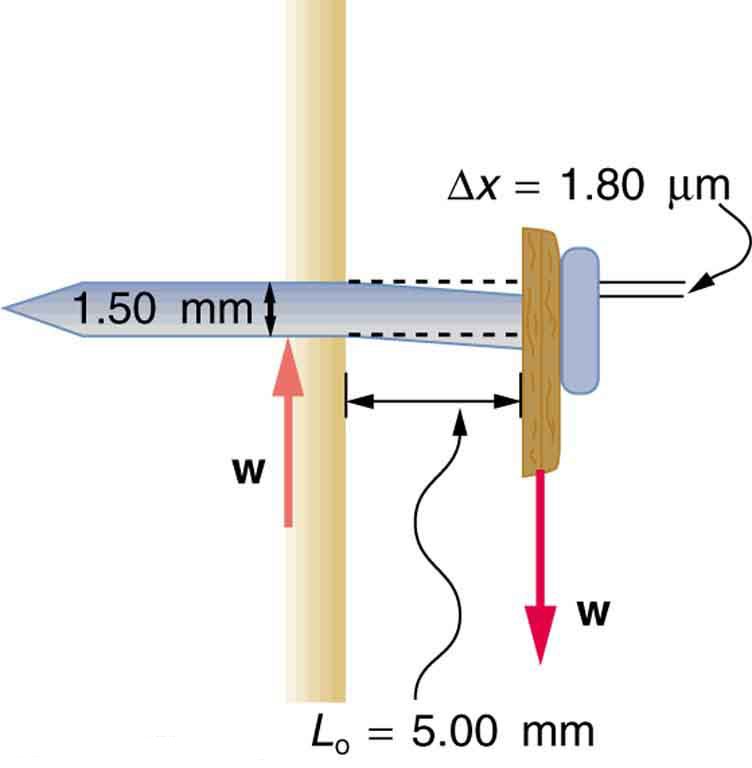
Find the mass of the picture hanging from a steel nail as shown in , given that the nail bends only .
Strategy
This is a fairly massive picture, and it is impressive that the nail flexes only an amount undetectable to the unaided eye.
Frequently Asked Questions Faqs
Q1: Does Poissons ratio is dependent on temperature?
Ans: In general, Colder temperature decreases both strains and high-temperature increases both horizontal and vertical strain. Thus, the net effect on Poissons Ratio is small since the change in both horizontal and vertical strain is by a similar amount.
Q2: Is Poissons ratio constant?
Ans: Poissons ratio for material remains approximately constant within elastic limits
Q3: Define Poissons ratio
Ans: The ratio of transverse strain to longitudinal strain in the direction of the stretching force.
Q4: Write the Poissons ratio formula
Ans:\
Q5: State true or False. Poissons ratio is negative for Tensile deformation.
Ans: False. Poissons ratio is Positive for Tensile deformation
Q6: What is Poissons ratio of concrete?
Ans: The Poissons ratio of concrete is 0.1 to 0.2.
Q7: What does the Poissons ratio 0.5 mean?
Ans: Poissons ratio 0.5 means a perfectly in-compressible material is deformed elastically at small strains.
Q8: What are the units of Poissons ratio?
Ans: Poissons ratio is the unitless scalar quantity.
Q9: What is Poissons ratio of cork?
Ans: Poissons ratio of cork is 0.0.
Hope you have understood Poissons ratio, how it is defined, its symbol, units, formula, terms and values for various materials.
Physics Related Topics:
Recommended Reading: What Does Amu Mean In Chemistry
What Is Youngs Modulus
Youngs modulus is also known as modulus of elasticity and is defined as:
The mechanical property of a material to withstand the compression or the elongation with respect to its length.
It is denoted as E or Y.
Youngs Modulus , is a measure of mechanical properties of linear elastic solids like rods, wires, and such. There are other numbers that give us a measure of elastic properties of a material, like Bulk modulus and shear modulus, but the value of Youngs Modulus is most commonly used. This is because it gives us information about the tensile elasticity of a material .
Youngs modulus describes the relationship between stress and strain . The Youngs modulus is named after the British scientist Thomas Young. A solid object deforms when a particular load is applied to it. If the object is elastic, the body regains its original shape when the pressure is removed. Many materials are not linear and elastic beyond a small amount of deformation. The constant Youngs modulus applies only to linear elastic substances.
Example : Calculating Change In Volume With Deformation: How Much Is Water Compressed At Great Ocean Depths
Calculate the fractional decrease in volume for seawater at 5.00 km depth, where the force per unit area is\boldsymbol^2}.
Strategy
Equation\boldsymbol=\frac\fracV_0}is the correct physical relationship. All quantities in the equation except\boldsymbol}}are known.
Solution
Solving for the unknown\boldsymbol}}gives
Substituting known values with the value for the bulk modulus\boldsymbolfrom Table 3,
Discussion
Although measurable, this is not a significant decrease in volume considering that the force per unit area is about 500 atmospheres . Liquids and solids are extraordinarily difficult to compress.
Conversely, very large forces are created by liquids and solids when they try to expand but are constrained from doing sowhich is equivalent to compressing them to less than their normal volume. This often occurs when a contained material warms up, since most materials expand when their temperature increases. If the materials are tightly constrained, they deform or break their container. Another very common example occurs when water freezes. Water, unlike most materials, expands when it freezes, and it can easily fracture a boulder, rupture a biological cell, or crack an engine block that gets in its way.
Other types of deformations, such as torsion or twisting, behave analogously to the tension, shear, and bulk deformations considered here.
Read Also: Elton John Kids Adopted
Relation Between Y K And
Y = 3K Y = 2 = \ \ or Y = \
Important Points
- For the same material, the three coefficients of elasticity , and K have different magnitudes.
- Isothermal elasticity of a gas E = p where, p = pressure of the gas.
- Adiabatic elasticity of a gas Es = pwhere, y = \, ratio of specific heats at constant pressure and at constant volume.
- Ratio between isothermal elasticity and adiabatic elasticity \
Elasticity:Elasticity defines a property of an object that has the ability to regain its original shape after being stretched or compressed. Learn about the deforming force applied on an elastic object and how the stress and strain works on an object. What is a Hookes law and how it is applicable for the concept of elasticity.
Example : Calculating Deformation: How Much Does Your Leg Shorten When You Stand On It
Calculate the change in length of the upper leg bone when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 40.0 cm long and 2.00 cm in radius.
Strategy
The force is equal to the weight supported, or
and the cross-sectional area is\boldsymbol^2=1.257\times10^\textbf^2}.The equation\boldsymbol=\frac\fracL_0}can be used to find the change in length.
Solution
All quantities except\boldsymbol}are known. Note that the compression value for Youngs modulus for bone must be used here. Thus,
Discussion
This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 3 have larger values of Youngs modulus\boldsymbol.In other words, they are more rigid.
The equation for change in length is traditionally rearranged and written in the following form:
The ratio of force to area,\boldsymbol},is defined as stress, and the ratio of the change in length to length,\boldsymbol}},is defined as strain . In other words,
In this form, the equation is analogous to Hookes law, with stress analogous to force and strain analogous to deformation. If we again rearrange this equation to the form
we see that it is the same as Hookes law with a proportionality constant
Also Check: Who Is Paris Jacksons Biological Father
What Is Stress In Physics
Stress is the force experienced by an object which can cause a change in the object. It is the force applied per unit area of an object. We can give the stress in physics as follows:
= F/A
When is stress, F is the force applied, and A is the area of the force application. The unit of measurement of stress is N/m2. There are two types of stress: they are tensile stress and compressive stress. Tensile stress is the force that acts on a unit area of material that can result in an increase in the length of the object. Therefore, the objects that are under tensile stress can become thinner and longer.
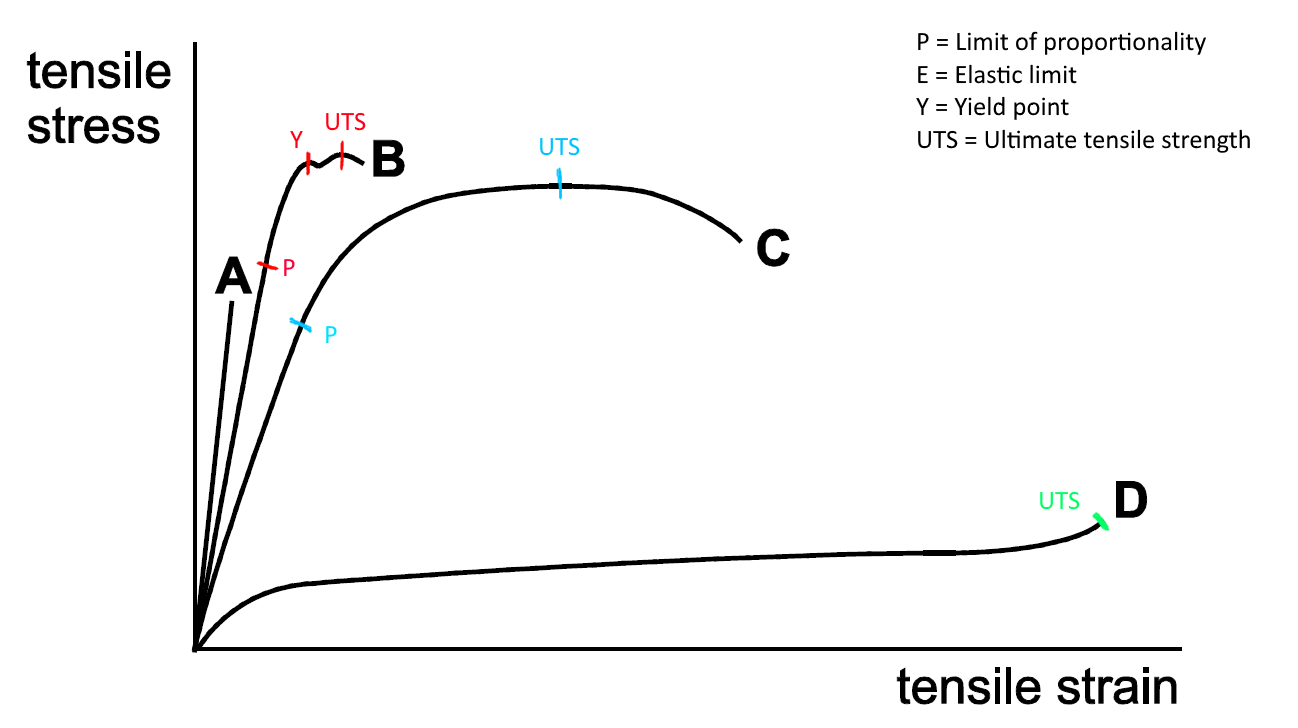
Stress vs Strain of Ductile Material
Compressive stress is the force acting on a unit area which can result in the decrease of length of the object. Therefore, the objects that are under this stress can become thicker and shorter.
Solved Problems On Strain
Q.1. A sample of biological material is loaded into a material-testing machine. The material is \ long in its unloaded state. However, under a tensile force of \ it stretches to a length of \ due to this force. What is the strain in the specimen when it is stretched this much?Ans: Initial length \ = 2\ }\)Final Length \ = 2.0004\ }\)Change in length \\\
Q.2. A girl stretches her rubber band of length \ such that its length increases by \. Compute the strain.Ans: Original length of rubber band \ = 6\ } = 0.06\ }\)Change in length \}\,}}\,}\)The strain is given by \\
Read Also: Blanket Jackson Real Parents
Comparison Summary Stress Vs Strain In Physics
Stress and strain in physics are related to each other, and they are directly proportional to each other up to the elastic limit of an object. The relationship between these two terms can be given using Hookes law. The key difference between stress and strain in physics is that stress is the force experienced by an object which causes a change in the object, whereas strain is the change in the shape of the object when stress is applied.
Reference:
1. Stress and Strain Definition, Stress-Strain Curve, Hookes Law, SI Units. , BYJUS, 24 Feb. 2021, Available here.
Image Courtesy:
1. Stress Strain Ductile Material By Breakeydown via Commons Wikimedia
What Is The Si Unit Of Youngs Modulus
Pascal is the SI unit of Youngs modulus.
Hope you have understood modulus of elasticity and Youngs modulus in this article. Stay tuned with BYJUS for more such interesting articles. Also, register to BYJUS The Learning App for loads of interactive, engaging Physics-related videos and an unlimited academic assist.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
You May Like: Abiotic Biology Definition
Elastic Modulus In Physics
Elastic Modulus formula:The modulus of elasticity is simply stress divided by strain:
E = \
E is Youngs Modulus is the uniaxial stress or uniaxial force per unit surface is the strain, or proportional deformation it is dimensionless
Elastic Modulus Dimensional Formula:
- SI Unit is pascals
- The practical units are megapascals or gigapascals .
Elastic Modulus Symbol:Elasticity modulus or Youngs modulus is a measure for the ratio between the stress applied to the body and the resulting strain.
Elasticity:Elasticity defines a property of an object that has the ability to regain its original shape after being stretched or compressed. Learn about the deforming force applied on an elastic object and how the stress and strain works on an object. What is a Hookes law and how it is applicable for the concept of elasticity.