Is Shear Strain An Additive Quantity
Consider a box with rigid walls containing an elasic medium, subject possibly to some body forces or tractions.
The volume is an additive quantity, in the sense that the total volume change of the system may be written as the sum of volume changes of subsystems. Therefore, if I define the strain tensor $\epsilon_$, then for any forcing carried out while holding the walls fixed, $$ \Delta V = \int \mathrm \, \mathrm} = 0.$$
Is there any analogous additivity for shear strain? Is it true that if the boundaries of the medium are fixed then $$ \int \mathrm \, \epsilon_ = 0?$$
Is it true more generally that, if the box is deformed to a parallelopiped with shear strain $\gamma$, then $$ \int \mathrm \, \epsilon_ = V \gamma?$$
Perhaps there is some theorem about integrating the gradient of a vector field which will help?
$$\int \mathrm \, \epsilon_ = \frac\int \mathrm \,\mathrm \,\mathrm\, \left,$$
and thus $$\int \mathrm \, \epsilon_ = \frac L^2 \left$$$$\int \mathrm \, \epsilon_ = \frac \gamma V.$$
I guess the factor of $1/2$ is the usual factor between the “engineering strain” and $\epsilon_$. But this still almost seems too simple to be true.
1) Is shear strain an additive quantity?____Yes, if in the same plane.
2) How do strains change a 3-volume?____Shear strains do not change the volume.$$M=e^$$
$$dV’=detdV$$where $det$ is the Jacobian of the transformation of coordinates from to .$$=detdV$$$$=e^dV$$$$=e^dV$$$$=e^+\epsilon^+\epsilon^)}dV$$
What Is Shearing Of The Skin
Friction injury occurs when the epidermis or top layer of skin separates from the dermis or bottom layer of skin. This is what is often referred to as a rug burn. Shearing is pressure and friction, injuring the skin at the same time. It happens more often than people realize because it is so easy to occur.
Shear Strain At Corners And Edges Of Epitaxial Silicon On Sapphire
49bTx
REFERENCESSection:
Recommended Reading: Bridge To Algebra Pizzazz
Shear Stress And Shear Strain
Lets consider a Rivet is used to join two plates as shown in the figure. When two equal forces are acting on the two plates in opposite direction. Then a shear force is acted on the rivet and a shear stress will be induced at the cross-section of the rivet. If this load or force crosses the elastic limit then the rivet will fail as shown in the following fig.
This Shear stress can be calculated as the ratio of Tangential force acting on the Rivet to the Crossection area of the Rivet.
Mathematically
Shear stress = Tangential Force/ Resisting cross-sectional Area.
Shear strain can be defined as the ratio of deformation to its original length or shape.
Shear strain can be represented by
Here the shear stress directly proportional to the Shear strain within the elastic limit.
Shear Stress Shear Strain
Where C= Constant of Proportionality Known the Modulus of rigidity or Shear Modulus.
Kids Work And What Is Strain Physics
These greater shear forces increase the danger of back injury through ruptured discs. A greater modulus typically signals that the material is more order dissertation online difficult to deform. Such pairs may also be called power conjugate or employment conjugate tension and strain measures. The refractive index in any particular direction through the crystal is regulated by the dielectric constant Kij that is a tensor.
As an example, push the surface of a book resting on a tabletop so the force is parallel to surface. Consider a unit sphere that has been deformed. In case the material is elastic, the object will go back to its initial form and size whenever these forces are removed. If theres an increase in length of the material line, the standard strain is known as tensile strain, otherwise, if theres reduction or compression in the amount of the material line, its called compressive strain.
To explain the reason why this step is a significant one, we have to consider what is required for the building of a quantum computer. You are able to even build sophisticated computer models to aid you. They are extremely ductile, making them hard to machine. If theres an increase in length of the material line, the standard strain is known as tensile strain.
Don’t Miss: What Was The Climate Like In The New England Colonies
Shear Stress Strain And Modulus
The concepts of shear stress and strain concern only solid objects or materials. Buildings and tectonic plates are examples of objects that may be subjected to shear stresses. In general, these concepts do not apply to fluids.
Shear deformation occurs when two antiparallel forces of equal magnitude are applied tangentially to opposite surfaces of a solid object, causing no deformation in the transverse direction to the line of force, as in the typical example of shear stress illustrated in . Shear deformation is characterized by a gradual shift \textx of layers in the direction tangent to the acting forces. This gradation in \textx occurs in the transverse direction along some distance _. Shear strain is defined by the ratio of the largest displacement \textx to the transverse distance _
Shear strain is caused by shear stress. Shear stress is due to forces that act parallel to the surface. We use the symbol _ for such forces. The magnitude _ per surface area A where shearing force is applied is the measure of shear stress
The shear modulus is the proportionality constant in and is defined by the ratio of stress to strain. Shear modulus is commonly denoted by S:
What Is Strain Physics: The Ultimate Convenience
Hookes Law states that for smaller deformities, the tension and strain are proportional to one another. Contraction ways to secure shorter. Hence, even if the stress is zero, the strain isnt zero and the deformation is known as plastic deformation. In the area from A to C strain and strain arent proportional.
As an example, push the surface of a book resting on a tabletop so the force is parallel to surface. Consider a unit sphere that has been deformed. Its a dimensionless quantity as its a ratio between two quantities of same dimension. If theres an increase in length of the material line, the standard strain is known as tensile strain, otherwise, if theres reduction or compression in the amount of the material line, its called compressive strain.
Don’t Miss: Cosine In Physics
Behaviour Of Soil During Shearing
Figure 7A shows a block of soil with a constant normal effective stress subjected to an increasing shear stress .
Figure 7. Shearing of soil.
The soil is drained and it distorts with a shear strain and a volumetric strain v. If the soil is undrained, there are no volume changes but the pore pressures change. The block of soil represents conditions inside a slip zone in the slope illustrated in Figure 7B or in a foundation illustrated in Figure 7C. If the slope is created by excavation or erosion the normal stress decreases and, since soil strength is frictional, it will weaken, whereas below the loaded foundation the normal stress increases and the soil becomes stronger.
The behaviour of soil initially loose and initially dense of critical is illustrated in Figure 8. The loose soil compresses during shearing even though the normal stress remains constant and the dense soil dilates. The rate of dilation is given by an angle of dilation , given by
Figure 8. Stress and volume change in shearing soil.
Tomy Varghese, in, 2020
Shearing Stress In Fluids
Shear stress is observed in fluids too. When a fluid flows within the boundary of solids, the shear stress is observed along with the point of contact between fluid and boundary. Fluid comprises of various levels, each level travel at different speeds. The layers which are at the same height from the boundary experience same speed. This varying speed between the layers is also a result of shear stress. In fluids, stress and strain are related differently. Here, shear stress is proportional to strain rate with viscosity as proportionality constant.
You May Like: Eoc Fsa Practice Test Answers
Mechanical Behavior Of Materials
Clearly, stress and strain are related. Stress and strain are related by a constitutive law, and we can determine their relationship experimentally by measuring how much stress is required to stretch a material. This measurement can be done using a tensile test. In the simplest case, the more you pull on an object, the more it deforms, and for small values of strain this relationship is linear. This linear, elastic relationship between stress and strain is known as Hooke’s Law. If you plot stress versus strain, for small strains this graph will be linear, and the slope of the line will be a property of the material known as Young’s Elastic Modulus. This value can vary greatly from 1 kPa for Jello to 100 GPa for steel. For most engineering materials, the linear region of the stress-strain diagram only occurs for very small strains . In this course, we will focus only on materials that are linear elastic and isotropic .
From Hooke’s law and our definitions of stress and strain, we can easily get a simple relationship for the deformation of a material.
Intuitively, this exam makes a bit of sense: apply more load, get a larger deformation apply the same load to a stiffer or thicker material, get less deformation. If the structure changes shape, or material, or is loaded differently at various points, then we can split up these multiple loadings using the principle of superposition.
Tensile Or Compressive Stress Strain And Youngs Modulus
Tension or compression occurs when two antiparallel forces of equal magnitude act on an object along only one of its dimensions, in such a way that the object does not move. One way to envision such a situation is illustrated in . A rod segment is either stretched or squeezed by a pair of forces acting along its length and perpendicular to its cross-section. The net effect of such forces is that the rod changes its length from the original length _ that it had before the forces appeared, to a new length L that it has under the action of the forces. This change in length \textL=L-_ may be either elongation or contraction . Tensile stress and strain occur when the forces are stretching an object, causing its elongation, and the length change \textL is positive. Compressive stress and strain occur when the forces are contracting an object, causing its shortening, and the length change \textL is negative.
In either of these situations, we define stress as the ratio of the deforming force _ to the cross-sectional area A of the object being deformed. The symbol _ that we reserve for the deforming force means that this force acts perpendicularly to the cross-section of the object. Forces that act parallel to the cross-section do not change the length of an object. The definition of the tensile stress is
Recommended Reading: Practice 2-4 Reasoning In Algebra Answers
Shear In Fluids: What Is Measured And Called
- 67
- 4
- 21,727
- 4,934
- 4
is velocityh is heightRate then is in terms of distance from the bottom of the gap to whatever point you take. I would say, shear rate is 10m/s per 0.05mm. Or, 100m/s per 0.5mm. Whatever, the rate is the same. The unit for this shear rate then would be m/s per m.But shear rate is measured in reciprical seconds, 1/s. This is what I don’t comprehend. Why, if you have / h, do you measure rate of shear in reciprical seconds?That would mean the shear rate is simply a time measurement. Not seconds, but the reciprical.What am I not understanding. Thanks.
Shear Stress And Strain

- Sourced from MIT OpenCourseWare
No headers
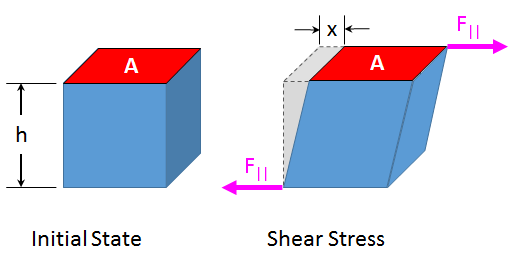
The surface of material may also be subjected to tangential forces producing a shearing action. Consider a block of height h and area A , in which a tangential force, \ is applied to the upper surface. The lower surface is held fixed. The upper surface will shear by an angle \ corresponding to a horizontal displacement \ The geometry of the shearing action is shown in Figure 26.5.
Figure 26.5: Shearing forces
The shear stress is defined to be the ratio of the tangential force to the cross sectional area of the surface upon which it acts,
\begin\sigma_=\frac}\end
The shear strain is defined to be the ratio of the horizontal displacement to the height of the block,
\begin\alpha=\frac\end
For many materials, when the shear stress is sufficiently small, experiment shows that a Hookes Law relationship holds in that the shear stress is proportional to shear strain,
\begin\frac}}=S \frac \quad \text \end
where the constant of proportional, \, is called the shear modulus. When the deformation angle is small, \, and Equation becomes
\begin\frac}} \simeq \ \alpha \quad \text \end
In Table 26.2, the shear modulus is tabulated for various materials.
Table 26.2: Shear Modulus for Various Materials
Example 26.1: Stretched wire
\beginF_=m g\end
We can calculate the strain on the wire from Hookes Law ) and the value of Youngs modulus for steel \\).
\begin\frac}=\frac}=\frac=\frac \mathrm\right)\left} \mathrm\right)\left}=5.3 \times 10^\end
Don’t Miss: Ccl4 Dot Structure
What Does Shear Strain Mean
Shear strain is the ratio of displacement to an objects original dimensions due to stress, and is the amount of deformation perpendicular to a given line rather than parallel to it.
In engineering, shear strain is the tangent of the angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application, which sometimes makes it easier to calculate.
Shear strain measures how much a given deformation differs from a rigid deformation. Shear strain is strain that results from the use of opposing forces in a parallel direction to the surface of an object. It is an angular change at some point in a shape.
Shear strain is the amount of contortion caused by the sliding of plane layers over each other within a deformity that can be applied by elongation, shortening, volume changes or angular distortion.
Shear strain can accelerate an objects corrosion rate.
What Is Shear Stress And Shear Strain
April 9, 2018 by Sundar
In a Machine, every component subjected to various forces. Due to these forces acting on the machine components, there are various types of stresses are induced. Where a simple stress is defined as the internal resistance force that opposes the external force per unit area. Where the Strain is defined as the deformation per unit length. Shear stress and shear strain are also defined in the same way. Lets see How we can define them?
When a body is subjected to two equal and opposite forces acting tangentially, across the resisting section, then the body tends to shear off the section. The stress induced in the section is known as the shear stress.
Make sense? Ok. lets take an example to understand the scenario.
Don’t Miss: Geometry Segment Addition Postulate Worksheet
Ratios Proportions And Angles
Dimensionless quantities are often obtained as of that are not dimensionless, but whose dimensions cancel out in the mathematical operation. Examples include calculating or . A more complex example of such a ratio is , a measure of physical deformation defined as a change in length divided by the initial length. Since both quantities have the dimension length, their ratio is dimensionless. Another set of examples is or often written using such as ppm , ppb , and ppt , or perhaps confusingly as ratios of two identical units ” rel=”nofollow”> mol/mol). For example, , which characterizes the concentration of in an , could be written as mL / 100 mL.
Other common proportions are percentages , and angle units such as , . In the is the ratio of the to the and is used to measure the in the .
It has been argued that quantities defined as ratios Q = A/B having equal dimensions in numerator and denominator are actually only unitless quantities and still have physical dimension defined as dim Q = dim A × dim B1.For example, may be defined as a ratio of volumes or as a ratio of masses both would be unitless quantities, but of different dimension.
Shear Modulus And Shear Strain Relationship
- 38
- 0
- 7,002
- 294
AlephZero said:It’s not clear if you have given all the data that was in the question, or just what you thought was relevant.If you apply a shear force to a cantilever beam, you probably get other stresses as well as the shear stress, and the other stresses are often much bigger.
No, the shear modulus does not tell you about the shear resistance.Same as Young modulus does not tell about tensile resistance.They just determine how much will be the strain at a given stress.What you need is some information about the maximum shear strain of the material.
Don’t Miss: How To Find Half-life Of A Reaction