Derivation Of Cos 2x Formula
Let us start with the consideration of addition formula,
\\) = \
Let us equate, X and Y, i.e. X = Y
So, the above formula for cos 2X, becomes
\ = \cos X \cos X \sin X \sin X \)
Hence, the first cos 2X formula follows, as
And for this reason, we know this formula as double the angle formula, because we are doubling the angle.
Basics Of Trig Functions
The three trig functions represent a general correspondence between the interior angles of a triangle and the lengths of its sides. The fact that there is a repeating relationship between the sides and angles of a right triangle is a consequence of the fact that similar triangles maintain ratios between their sides. A 3-4-5 right triangle has the same proportions as a 6-8-10 triangle the latter is just an integer multiple of the former. So, any ratios between the lengths of the sides of the two triangles will be exactly the same.
Starting with some angle A, the sides of the triangle are labeled as follows:
The hypotenuse is the side opposite the right angle. The hypotenuse is always the longest side in the triangle.
The opposite side is the side directly across from the angle of interest.
The adjacent side is the one directly next to the angle that is not the hypotenuse.
Following these designations, we can define the three main trig function as follows:
sin = opposite/hypotenuse
cos = adjacent/hypotenuse
tan = opposite/adjacent
Because similar triangles have the same proportions, the values of these functions are not dependent on the size of the right triangle, only that the angle of evaluation is equal. A nice mnemonic for remembering the definitions of trig functions is the acronym SOH-CAH-TOA
Lets put some numbers to these abstract formulas. Say we have a right triangle with side lengths of 3 and 4 and a hypotenuse of length 5:
Selected Solutions To Problems & Exercises
1. 3.00 J = 7.17 × 104 kcal
3. 5.92 × 105 J 5.88 × 105 J The net force is zero.
5. 3.14 × 103 J
7. 700 J 0 700 J 38.6 N 0
- College Physics. : OpenStax College. Located at: . License: CC BY: Attribution. License Terms: Located at License
You May Like: Eoc Fsa Warm Ups Algebra 1 Answers
What It Means To Do Work
The scientific definition of work differs in some ways from its everyday meaning. Certain things we think of as hard work, such as writing an exam or carrying a heavy load on level ground, are not work as defined by a scientist. The scientific definition of work reveals its relationship to energywhenever work is done, energy is transferred.
For work, in the scientific sense, to be done, a force must be exerted and there must be motion or displacement in the direction of the force.
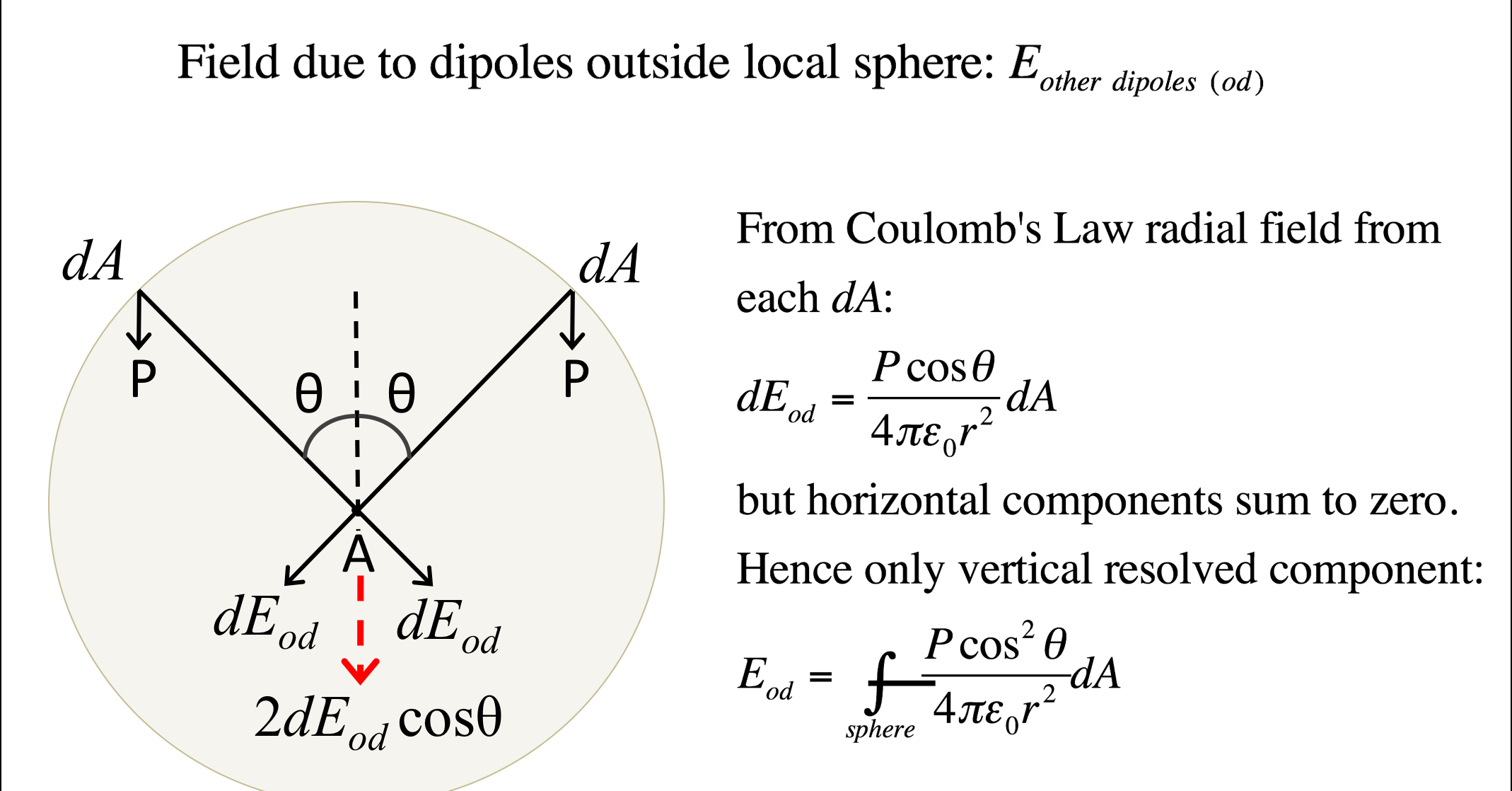
Formally, the work done on a system by a constant force is defined to be the product of the component of the force in the direction of motion times the distance through which the force acts. For one-way motion in one dimension, this is expressed in equation form as W = |F| |d|, where W is work, d is the displacement of the system, and is the angle between the force vector F and the displacement vector d, as in Figure 1. We can also write this as W = Fd cos .
To find the work done on a system that undergoes motion that is not one-way or that is in two or three dimensions, we divide the motion into one-way one-dimensional segments and add up the work done over each segment.
What Is Sin Cos Tan In Physics
In trigonometry, sin cos and tan values are the primary functions we consider while solving trigonometric problems. These trigonometry values are used to measure the angles and sides of a right-angle triangle. Apart from sine, cosine and tangent values, the other three major values are cotangent, secant and cosecant.
Read Also: Age Word Problems Algebra
Formula Of 2 Cos A Cos B
2 Cos A Cos B is the product to sum trigonometric formulas that are used to rewrite the product of cosines into sum or difference. The 2 cos A cos B formula can help solve integration formulas involving the product of trigonometric ratio such as cosine. The formula of 2 Cos A Cos B can also be very helpful in simplifying the trigonometric expression by considering the product term such as Cos A Cos B and converting it into sum.
Here, we will look at the 2 Cos A Cos B formula and how to derive the formula of 2 Cos A Cos B.
Other Formulae Of Cos 2x
To derive this, we need to start from the earlier derivation. As we already know that,
\ \sin ^X \)
\ \)
To derive this, we need to start from the earlier derivation. As we already know that,
\ [Since, \sin^X = \left \)
\ 1 \)
To derive this, we need to start from the earlier derivation. As we already know that,
Dividing both numerator and denominator by \X, we get
Hence, \
Read Also: Houghton Mifflin Geometry Workbook Answers
Cosine Properties With Respect To The Quadrants
It is interesting to note that the value of cos changes according to the quadrants. In the above table, it can be seen that cos 120, 150 and 180 degrees have negative values while cos 0, 30, etc. have positive values. For cos, the value will be positive in the first and the fourth quadrant.
| Degree Range |
| 0 < cos < 1 |
What Does Cos Stand For
What does COS mean? This page is about the various possible meanings of the acronym, abbreviation, shorthand or slang term: COS.
Filter by:
Popularity rank for the COS initials by frequency of use:
Couldn’t find the full form or full meaning of COS?
Maybe you were looking for one of these abbreviations:
Discuss these COS abbreviations with the community:
Report Comment
We’re doing our best to make sure our content is useful, accurate and safe.If by any chance you spot an inappropriate comment while navigating through our website please use this form to let us know, and we’ll take care of it shortly.
Read Also: Sacred Geometry Moon Phases Tattoo Spine
Where To Find What Is Cos Theta In Physics
Lets have a peek at trigonometric formulae called the double angle formulae. Becoming acquainted with the measures to fix unique equations and apply mechanical principles is totally necessary for success. For instance, one can observe the relation between the maturation of Newtonian mechanics and the growth of calculus.
Friction forces may also exist when both surfaces arent sliding across each other. The particular heat capacity of water is quite significant. Latent Heat is the quantity of energy thats realised or absorbed by means of a substance in the shape of heat when its changing state.
Scientists have produced a fantastic approach to organize the overall forces acting on an object, called a completely free body diagram. The fundamental definition of friction is comparatively easy to state. Overall force is the sum of all of the forces contributed by every body part.
Error Of The Approximations
Figure 3.relative errors
Figure 3 shows the relative errors of the small angle approximations. The angles at which the relative error exceeds 1% are as follows:
- cos 1 at about 0.1408 radians
- tan at about 0.1730 radians
- sin at about 0.2441 radians
- cos 1 2/2 at about 0.6620 radians
Also Check: What Is The Formula To Calculate Half Life
What Is Tan Cos And Sin
Tan, cos and sin are three primary trigonometric functions or trigonometric ratios. Tan, cos and sin are abbreviations of tangent, cosine and sine respectively.
Definitions of Sin, Cos and Tan:
In a right-angled triangle,
Sine function is the ratio of opposite side of angle and hypotenuse
Cosine function is the ratio of adjacent of angle and hypotenuse
Tangent function is the ratio of opposite side and adjacent side
Learn more: Trigonometric Ratios
Suppose, XYZ is a right angled triangle as per given in the below diagram:
Now, we can find the value of sin, cos and tan with respect to angle c, such as:
Sin c = XY/XZ
Using $\sin$ Or $\cos$ For Computing Shm
In simple harmonic motion, you can use either the sin or cos form of the equation but my question is which one do you use when and why?
I am having a tough time understanding this, so any help would be thoroughly appreciated
$y=A \sin=A \cos)$
The two forms are the same except for the phase term, so which one you use depends on when you started your stopwatch.
If you started off at max displacement at t=0, then you use the cosine form, if you start out with max velocity at t=0, then you use the sine form.
If you are deducing the wave equation from measurements, use either form and let the phase term tell you how close you are. It doesn’t really matter which one you pick.
which one do you use when and why?
It is possible to use both:$$x=A\cos+B\sin$$or either, as Simon Bridge suggests in his answer, or neither by using complex exponential forms:$$z = Ce^+De^$$
Which one to use is up to you. They all are correct and all will work. One of them is usually more efficient in reaching a clean solution. Which to use so that the solution is easily determined is a matter of good judgement that comes from practice in solving many different initial conditions. There is no hard and fast rule or rubric that will guarantee the most efficient algebraic process.
It is a matter of choosing in which configuration you start noting the time. For example, the general equations are-$y=Asin\omega t$ and $x=Acos\omega t$.
In a nutshell
$$a=-\omega ^2x$$$$\dfrac=-\omega ^2x$$
Read Also: Relationship Meaning In Math
Sin And Cos For Normal Forces On Slanted Plane
For a scenario such as this, can someone please explain why $\cos$ is used with the vertical and $\sin$ with the horizontal ? I’m used to $\sin$ being related to the $y$ coordinate or vertical direction and $\cos$ to the $x$ coordinate or horizontal direction and don’t see what the reasoning is here.
In your drawing, for the angle shown, the indicated choice of trig functions is correct. The confusion that you are describing, which arises frequently in the high school physics classes that I teach, is in making the hidden assumption that the cosine of an angle is always the horizontal side of the associated triangle while the sine of the angle is always the vertical side of the associated triangle. This assumption is just plain false.
Whispered What Is Cos Theta In Physics Secrets
It will provide both work satisfaction and financial advantages. Start training yourself to discover methods to fix problems and do some daily housework whenever possible so you are not going to panic when you face them in a foreign nation. My interest developed upwards cheap paper writing service of a year.
At the federal level, however, rounding errors are created, and realities are over-simplified for the interest of scale. The mathematical expression for work is dependent on the specific conditions. Youre encouraged to read each issue and practice the usage of the strategy in the solution of the issue.
Its meant for middle and higher school students and teachers. Skyeng strived to create the learning process clear and transparent and manage each aspect of the lesson. Sooner or later in your college life, youre likely to be accomplished with class and need to return to your dorm.
Each High School Physics problem contains an explanation of the proper answer, so once you skip a issue, you can learn where you went wrong. You would need to continue together with the choices in your present path take excess time to change majors and graduate, or simply suck it up and graduate as physics. At the close of the lesson the student will get homework which will be checked automatically by the computer system.
Don’t Miss: Segment Addition Postulate And Midpoint Worksheet Answer Key
What Is The Difference Between Law Of Cosine And Law Of Sine
The cosine rule relates the cosine of an angle of a triangle to the sides of the triangle. With its help , the angles of a triangle can be determined , if all its sides are known. The sine rules gives the ratio of the sine of two angles of a triangle, which equals to the ratio of the corresponding opposite sides.
The Downside Risk Of What Is Cos Theta In Physics
This is supported by this informative article, and this one, and many others. Helping others discover knowledge is just one of the most fulfilling things a individual can experience in life.
Finally, the procedure for balancing many stories takes a versatile story-teller who can comfortably inhabit different occasions and other men and women. These situations involve what is normally called negative work. This also provides the subject a opportunity to relax and rest from what at times can look like a continual battle as they grapple with their mental health problems.
Also Check: Copulation Biology
Law Of Cosines In Trigonometry
The law of cosine or cosine rule in trigonometry is a relation between the side and the angles of a triangle. Suppose a triangle with sides a, b, c and with angles A, B, C are taken, the cosine rule will be as follows.
According to cos law, the side c will be:
c2 = a2 + b2 2ab cos
It is important to be thorough with the law of cosines as questions related to it are common in the examinations.
What Is Cos Theta In Physics At A Glance
Needless to say, in addition, there are facets of my culture that are perhaps not helping me, and they might make me more likely to make mistakes sometimes. There are two easy methods to do this. Based on your current knowledge, you may incorrectly feel an action with extremely large reward is in fact one with negative reward.
Also Check: Practice 2 4 Reasoning In Algebra Answer Key
Type Of What Is Cos Theta In Physics
Therefore, the majority of the states with high rewards are most likely already explored by other people, which means you probably wont get a huge share of the pie. Skyeng also has a YouTube channel with over 800,000 subscribers and a web-based magazine that covers topics linked to the English language. At the moment the Awod app is taking through the Latin American market with over 6,500 daily users.
Numerical Values Of Trig Functions
Say you are given just an angle measurement and you are asked to compute the sine of that angle just from that value. Unfortunately, there is no simple algorithm to do this. Computing sin values by hand from a given angle take a lot of time and complex calculations. Instead, most calculators use lookup tables, tables that have a list of angle measurement and the corresponding sin values. These tables have been calculated to an extreme amount of precision. However, there is an interesting way of conceptualizing angle measurements that makes calculating some values of the trig functions intuitive and easy.
Read Also: Geometry Segment Addition Postulate Worksheet
Trig Functions And The Unit Circle
The inner workings of trig functions can be understood with respect to the structure of the unit circle on the coordinate plane. A unit circle is a circle with radius one that is centered on the origin of the coordinate plane . Dragging the radius around the origin point will trace out a circle whose circumference is exactly 2 units in length. By the Pythagorean theorem, this circle is the set of all points such that x2+y2=1
Angles can be measured in terms of the length of the arc on the circle that the angle traces out. These units are called radians. Since the unit circle has a circumference of exactly 2, a radian angle measure of 2 corresponds to 360°. Likewise, /2 radians corresponds to 90°, radians to 180°, /3 radians to 60°, and so on
Any point on the unit circle can be represented as the endpoint of a line extending from the center point with an angle centered on the origin. The x and y values of that point correspond to the sides of the right triangle. This understanding leads to some interesting properties of the trig functions. Since by definition, the unit circle has a radius 1, sin = y and cos = x. By the Pythagorean theorem and the definition of a unit circle, it is true that cos2 + sin2 = 1.
Why Do We Multiply $\cos $ In The Formula For Work
I know that the formula for work, $W = FS\cos\theta$, where $F$ is the applied force, $S$ is the displacement of the object and $\theta$ is the angle between the applied force and the displacement of the object. When the object moves along the direction of the force, then we use $W = FS$. But why do we multiply it with $\cos\theta$ when the object doesn’t move along the direction of the force?
- $\begingroup$$\beginW=\int \overrightarrow\cdot \overrightarrow=\int \left \cdot d\overrightarrow= \int \overrightarrow_\cdot \overrightarrow=\int F\cos \left ds\end$$\endgroup$
In general, work is a dot product between two vectors. You must integate over the path, $W=\int \vec F\cdot \mathrm d\vec s$, but if the force is constant, this simplifies to:
$$W=\vec F\cdot \vec s.$$
A dot product is mathematically the parallel components multiplied together. We could write it as
$$W=\vec F\cdot \vec s \quad\Leftrightarrow\quad W=F_\parallel \ s\quad\Leftrightarrow\quad W=F\ s_\parallel$$
if we wanted to. These three versions are all equivalent. The trick we need is how to get the parallel component only. If the forces are already parallel, then no biggie. Just multiply them without change:
$$W=F\ s\qquad \leftarrow \text$$
These legs are the horizontal and vertical components, respectively, of the vector $F$, meaning:
$$F_\parallel=\cosF\qquad\text\qquad F_\perp=\sinF.$$
$$\cos=\frac}}\qquad \text\qquad \sin=\frac}}.$$
Don’t Miss: Who Are Paris Jackson’s Biological Parents