Part Ii: Age Word Problems Solvable With Two Variables
Example 6: The sum of Aaliyah and Haralds ages is 28. Four years from now, Aaliyah will be three times as old as Harald. Find their present ages.
Neither Aaliyah nor Haralds age is expressed in terms of the other. So for this problem, we will be using more than one variable to represent the unknown values. To start,
- Let }} be Aaliyahs age
- Let }} be Haralds age
Since they will be 4 years older in the next 4 years, we simply have to add 4 to their current ages to represent their future ages.
Looking back at our problem, there are two significant statements that can help us find our answers.
1) The sum of Aaliyah and Haralds ages is 28.
From this statement, we can create the equation below:
2) Four years from now, Aaliyah will be three times as old as Harald.
Meanwhile, the statement above can be translated into the following equation:
We now have two equations to solve.
- Equation 1:a + h = 28
- Equation 2:a + 4 = 3
First, well use equation 1 to solve for a.
Next, well replace a with 28 – h in equation 2.
Perfect! We are able to find the values for both our unknown variables, a and h, which also stand for the present ages for Aaliyah and Harald. So we have,
- Aaliyahs present age: a = 28 – h = 28 – 5} = }
- Haralds present age: h = }
Answer: Currently, Aaliyah is 23 years old while Harald is 5 years old.
Answer Check:
- Let }} be Jayas age
- Let }} be Nadias age
We then need to subtract 7 from their current ages to represent how old they were seven years ago.
Answer Check:
How To Easily Make Your Own Math Word Problems & Word Problems Worksheets
Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:
- Link to Student Interests:;By framing your word problems with student interests, youll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
- Make Questions Topical:;Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
- Include Student Names:;Naming a questions characters after your students is an easy way make subject matter relatable, helping them work through the problem.
- Be Explicit:;Repeating keywords distills the question, helping students focus on the core problem.
Dont:
- Test Reading Comprehension:;Flowery word choice and long sentences can hide a questions key elements. Instead, use concise phrasing and grade-level vocabulary.
- Focus on Similar Interests:;Framing too many questions with related interests — such as football and basketball — can alienate or disengage some students.
- Feature Red Herrings:;Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.
A key to differentiated instruction, word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.
Solving Age Word Problems
Example
In ???18???;years Sasha will be ???4???;times older than she is now.;How old is she now?
Because Sasha will be four times older in ???18???;years, we can relate her age now, ???s???;to her age in ???18???;years as ???4s???.
So we can write the equation ???s+18=4s???.
We can also organize the information by making a table.
Now solve for ???s???;in the equation.
???s+18=4s???
???18=3s???
???6=s???
Sasha is ???6???;now and in ???18???;years shell be ???4???;or ???24???;years old.
Lets do an example with more than one person.
One helpful way to organize these types of problems is by making a table.
Example
Because April is ???12???;years older than Eric, we can write
???A=E+12???
Because April will be twice as old as Eric in five years, we need to double Erics age in ???5??? years to get Aprils age in five years. The next equation is
???2=A+5???
This is a table that summarizes their ages and our equations:
Now you can substitute ???E+12???;for ???A???;into ???2=A+5???;and simplify.
???2=+5???
Read Also: The Segment Addition Postulate Answer Key With Work
An Alternate Method For The Age Word Problem
;Deb Russell
No matter what word problem you’re presented with in algebra, there’s likely going to be more than one way and equation that’s right to figure out the correct solution. Always remember that the variable needs to be isolated but it can be on either side of the equation, and as a result, you can also write your equation differently and consequently isolate the variable on a different side.
In the example on the left, instead of needing to divide a negative number by a negative number like in the solution above, the student is able to simplify the equation down to 2a = 48, and if he or she remembers, 2a is the age of Jan! Additionally, the student is able to determine Jake’s age by simply dividing each side of the equation by 2 to isolate the variable a.
Grade 9 Algebra Word Problems
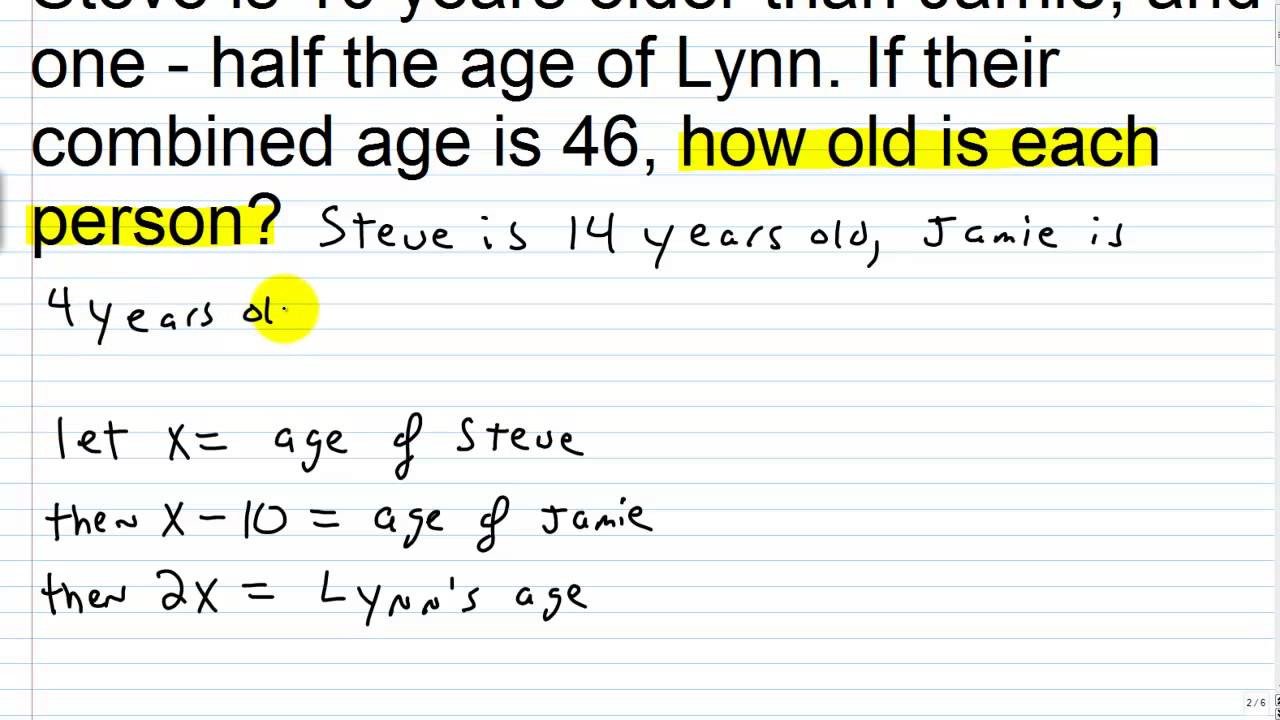
These lessons cover grade 9 algebra word problems involving age, distance, rate, time and coins with examples and step-by-step solutions? Includes various examples and solutions for algebra word problems that you will commonly encounter in grade 9.
Related Pages
Age Problems with two unknowns or variables
Example:Taylor is five times as old as Spenser. The sum of their ages is eighteen. How old are Taylor and Spencer?
Solution:Let x represent Spensers ageTherefore, Taylors age is 5xx + 5x = 18
Grade 9 Algebra Word Problems – Age
Example 1:A mother is three times as old as her daughter. Six years ago, the mothers age was six tines that of her daughter. How old are they now?
Solution:Let x represent the daughters age.Therefore, 3x is the mothers age.6 = 3x – 6Therefore, the daughters is 10 years old and the mother is 30 years old.
Example 2:A father is now three times as old as his son. Eight years ago, the father was five times as old as his son. How old are they now?
Grade 9 Algebra Word Problems – Rate, Distance, Time
Example:A bus leaves the terminal and averages 40 km/hr. One hour late, a second bus leaves the same terminal and averages 50 km/hr. In how many hours will the second bus overtake the first?
Grade 9 Rate, Distance, Time Word Problems
Example 1:One motorist travels 5 km.hr faster than another. They leave from the same place and travel in opposite directions. What is the rate of each if they are 195 km apart after 3 hours?
Don’t Miss: What Does Abiotic Mean
Math Word Problems To Challenge Students Grades 1 To 8
Category
- Teaching Tools
You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.
A jolt of creativity would help. But it doesnt come.
Whether youre a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.
This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes.
There are 120 examples in total. Helping you sort through them to find questions for your students, the resource is categorized by the following skills with some inter-topic overlap:
The list of examples is supplemented by;tips to create engaging and challenging math word problems.
Problem : Ratio Of Mixtures
In what ratio must a peanut costing $240 per kilogram be mixed with a peanut costing $340 per kilogram so that a profit of 20% is made by selling the mixture at $360 per kilogram?
Solution
a. Let x be the quantity of $240 per kilogram and y be the quantity of $340 per kilogram of peanuts. Write an equation for the capital and total sales.
Capital = 240x + 340yTotal sales = 360 Total sales = 360x + 360y
b. The formula for profit is:
Profit = Total Sales - CapitalProfit = - Profit = 120x + 20y
c. Since profit is 20% of the capital, the equation would be:
120x + 20y = 0.20 120x + 20y = 48x + 68y72x = 48y
d. Write the ratio of x and y variables.
/ = 48 / 72 / = 2 / 3
Final Answer: The final ratio is 2/3.
Read Also: Holt Geometry Lesson 4.5 Practice B Answers
Birthday Algebra Age Problem
;Deb Russell
In the following word problem, students are asked to identify the ages of both of the people in question by giving them clues to solve the puzzle. Students should pay close attention to key words like double, half, sum, and twice, and apply the pieces to an algebraic equation in order to solve for the unknown variables of the two characters’ ages.
Check out the problem presented to the left: Jan is twice as old as Jake and the sum of their ages is five times Jake’s age minus 48. Students should be able to break this down into a simple algebraic equation based on the order of the steps, representing Jake’s age as a and Jan’s age as 2a: a + 2a = 5a – 48.
Final Thoughts About Math Word Problems
Youll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, theyll be more relevant to — and engaging for;– your students.
Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.
The result?
A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.
Prodigy
Recommended Reading: Angle Addition Postulate Practice
Physical Measurement Word Problems
Best for: 1st grade, 2nd grade, 3rd grade, 4th grade
72. Comparing Measurements: Cassandras ruler is 22 centimetres long. Aprils ruler is 30 centimetres long. How many centimetres longer is Aprils ruler?
73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?
74. Adding Measurements: Michas dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Michas dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?
75. Subtracting Measurements: Michas dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Michas dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?
76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?
77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?
78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?
Problem : Father And Son’s Ages
Two times the father’s age is eight more than six times the son’s age. Ten years ago, the sum of their ages was 36 years. The age of the son is:
Solution
a. Let x be the age of the son and y be the age of the father.
2y = 6x + 8y = 3x + 4
b. Create a mathematical relation between the father’s age and the son’s age ten years ago.
+ = 36x + y = 56
c. Substitute the value of y into the equation x + y = 56.
x + y = 56y = 3x + 4x + = 564x + 4 = 564x = 56 -44x = 52x = 13
Final Answer: The son’s age is 13 years old.
Don’t Miss: Segment Addition Postulate Find The Length Indicated
Probability And Data Relationships Word Problems
Best for: 4th grade, 5th grade, 6th grade, 7th grade
89. Understanding the Premise of Probability: John wants to know his classs favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?
90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?
91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.
92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?
93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Mauritas 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felices 4 tests: 3, 3, 3. If Mauritas mean for the 4 tests is 1 point higher than Felices, whats the score of Felices 4th test?
94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?
Problem : Comparison Of Ages

Peter is 24 years old. Peter is twice as old as John was when Peter was as old as John is now. How old is John?
Solution
a. Let x be the present age of John. The table shows the relationship between their past and present ages.
Past and Present Ages of Peter and John
b. Create a mathematical equation for both steel and nickel. Then, create an equation for the summation of mixtures.
Steel:x + y = 2000y = 2000 - xMixture 1 + Mixture 2 = Final Mixture14x + 6y = 8 7x + 3y = 8000
c. Substitute equation 1 to equation 2.
7x + 3 = 8000x = 500 kg
Final Answer: 500 kg of steel containing 14% nickel is needed.
Also Check: Exponential Growth And Decay Common Core Algebra 1 Homework Answer Key
Quadratic Word Problems: Age And Numbers
Quadratic-based word problems are the third type of word problems covered in MATQ 1099, with the first being linear equations of one variable and the second linear equations of two or more variables. Quadratic equations can be used in the same types of word problems as you encountered before, except that, in working through the given data, you will end up constructing a quadratic equation. To find the solution, you will be required to either factor the quadratic equation or use substitution.
Example 10.7.1
The sum of two numbers is 18, and the product of these two numbers is 56. What are the numbers?
First, we know two things:
This means that Joey is 10 years old and Sally is 30 years old.
How To Solve Age Word Problems
If the problem involves a single person, then it is similar to an Integer Problem. Read the problem carefully to determine the relationship between the numbers. This is shown in the examples involving a single person.
If the age problem involves the ages of two or more people then using a table would be a good idea. A table will help you to organize the information and to write the equations. This is shown in the examples involving more than one person.
How To Solve Age Problems Involving A Single Person?
Example:Five years ago, Johns age was half of the age he will be in 8 years. How old is he now?
Solution:Step 1: Let x be Johns age now. Look at the question and put the relevant expressions above it.
Step 2: Write out the equation.
<img loading=lazy src=”/image-files/age-problem-equation-1.gif” alt=age problem equation title=age problem equation”width=104 height=85>
Answer: John is now 18 years old.
How To Use Algebra To Solve Age Problems?
Examples:
How To Solve Age Problems Involving More Than One Person?
Example:John is twice as old as his friend Peter. Peter is 5 years older than Alice. In 5 years, John will be three times as old as Alice. How old is Peter now?
Solution:Step 1: Set up a table.
| age now |
|---|
Write the new relationship in an equation using the ages in 2 yrs.
Recommended Reading: Exponential Growth And Decay Worksheet Algebra 1
Ratios And Percentages Word Problems
Best for: 4th grade, 5th grade, 6th grade
82. Finding a Missing Number: The ratio of Jennys trophies to Merediths trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?
83. Finding Missing Numbers: The ratio of Jennys trophies to Merediths trophies is 7:4. The difference between the numbers is 12. What are the numbers?
84. Comparing Ratios: The schools junior band has 10 saxophone players and 20 trumpet players. The schools senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?
85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?
86. Determining Percent of Change:A decade ago, Oakvilles population was 67,624 people. Now, it is 190% larger. What is Oakvilles current population?
87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?
88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?