Radius Diameter And Circumference
The Radius is the distance from the center outwards.
The Diameter goes straight across the circle, through the center.
The Circumference is the distance once around the circle.
And here is the really cool thing:
When we divide the circumference by the diameter we get 3.141592654…which is the number
|
So when the diameter is 1, the circumference is 3.141592654… |
We can say:
Circumference = × Diameter
Circles Explanation & Examples
One of the important shapes in geometry is the circle. A geometry-based exam will have most of the questions consist of rectangles, triangles, and circles.
Weve all seen circles before. They have this perfectly round shape, which makes them perfect for hula-hooping! This article will explain what a circle is, its properties, and its parts.
How To Draw A Circle
In maths projects for class 10 on circles, the construction of a circle, all the properties and terminologies are explained in detail. To understand what circles are in simple terms, go through circles for class 10, and also try the following exercise
If youve selected sufficient points, you may notice that the shape is starting to resemble a circle and this is exactly what the definition of a circle is.
Also Check: Does Kamala Harris Have Any Biological Children
Circle Formulas In Math :
Area and circumference of a circle:
Here Origin of the circle = O , Diameter = D and Radius = r
Area of a circle = r 2 = D2 = 0.7854 D2Circumference of a circle = 2 r = D.
Area of circle = x Circumference x radius
A = x C x r
Diameter of a circle = .
Arc and sector of a circle:
Here angle between two radii is in degrees. . And sector of a circle AOB.Arc length of circle = x 2 r = r / 180
Area of the sector = x r2
If the angle is in radians, then
The area of the sector = r 2
Sector angle of a circle = / .
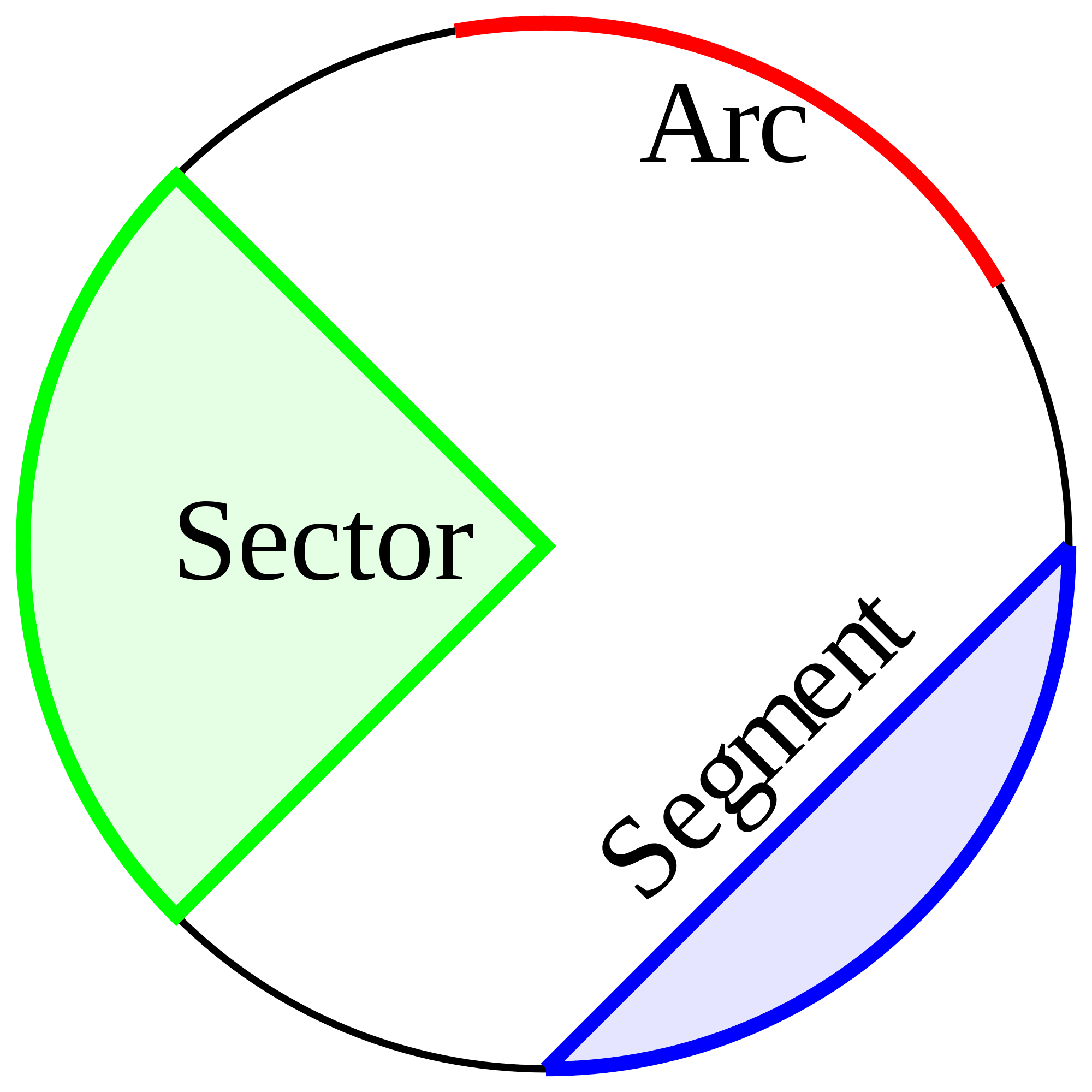
Segment of circle and perimeter of segment:
Here radius of circle = r , angle between two radii is in degrees.
Area of the segment of circle = Area of the sector Area of OAB.
Area of the segment = x r 2 x sin x r 2
Perimeter of the segment= + 2r sin .
Chord length of the circle = 2 = 2r sin .
Arc Length of the circle segment = l = 0.01745 x r x
Area of the circular ring:
Here big circle radius = R and Dia = D,
Small circle radius = r and Dia = d,
Area of a circular ring = 0.7854 =
Area of a circular ring = .
Formula for intersecting chords in circle:
Here AB and CD are two chords in circle and intersecting each at the point E.
Then AE : EB = DE : EC.
Bakers And A Mnemonic Device To Learn The Circumference And Area Definitions:
The real life example that I stop on is Bakers and how they use this with making pies. I bring in two fresh pies to illustrate my point. The reason for this is that I have a cute little mnemonic device to remember the actual formulas for circumference and area. For circumference, I show the class a cherry pie and teach them that “Cherry Pies Delicious” or C = D. And for area, I then show them an apple pie and teach them that “Apple Pies Are Too” or A = r2.
Now, we will measure the radius and the diameter of each pie and then will find out the area and circumference of both pies from finding both of these out and plugging them into both the formulas we just learned.
Apple Pie
You May Like: Why Are There Different Branches Of Chemistry
Yang Hui Magic Nine Circles In A Square
72 number from 1 to 72, arranged in nine circles of eight numbers in a square with neighbouring numbers forming four additional eight number circles: thus making a total of 13 eight number circles:
| NW | |
| S | SE |
Extra circle x1 contains numbers from circles NW, N, C, and W x2 contains numbers from N, NE, E, and C x3 contains numbers from W, C, S, and SW x4 contains numbers from C, E, SE, and S.
- Total sum of 72 numbers = 2628
- sum of numbers in any eight number circle = 292
- sums of three circles along horizontal lines = 876
- sum of three circles along vertical lines = 876
- sum of three circles along the diagonals = 876.
Chord Of A Circle Definition
The chord of a circle can be defined as the line segment joining any two points on the circumference of the circle. It should be noted that the diameter is the longest chord of a circle which passes through the center of the circle. The figure below depicts a circle and its chord.
In the given circle with O as the center, AB represents the diameter of the circle , OE denotes the radius of the circle and CD represents a chord of the circle.
Let us consider the chord CD of the circle and two points P and Q anywhere on the circumference of the circle except the chord as shown in the figure below. If the endpoints of the chord CD are joined to the point P, then the angle CPD is known as the angle subtended by the chord CD at point P. The angle CQD is the angle subtended by chord CD at Q. The angle COD is the angle subtended by chord CD at the center O.
Read Also: Unit 1 Test Geometry Basics Answers Key
Compass And Straightedge Constructions
There are many compass-and-straightedge constructions resulting in circles.
The simplest and most basic is the construction given the centre of the circle and a point on the circle. Place the fixed leg of the compass on the centre point, the movable leg on the point on the circle and rotate the compass.
Chord Of A Circle Theorems
If we try to establish a relationship between different chords and the angle subtended by them in the center of the circle, we see that the longer chord subtends a greater angle at the center. Similarly, two chords of equal length subtend equal angle at the center. Let us try to prove this statement.
Also Check: Example Of Span Linear Algebra
So How Can We Remember The Actual Circle Formulas
Once I briefly introduce these definitions, then I talk a bit about why in real life we would need to find area and circumference of a circle. I model on the smart board a google search about Real Life uses and show the top 5 according to Yahoo. They are as follows:
1. Car makers can measure car wheels to make sure they fit.2. Race car engineers can use it to find out what size tire gives them the most performance.3. Bakers can use it to make pies and other circular stuff.4. Military engineers can use them to balance helicopter blades.5. Aircraft engineer can use them for propeller efficiency.
How To Find Area Of A Circle
As we know, the area of circle is equal to pi times square of its radius, i.e. x r2. To find the area of circle we have to know the radius or diameter of the circle.For example, if the radius of circle is 7cm, then its area will be:Area of circle with 7 cm radius = r2 = 2 = 22/7 x 7 x 7 = 22 x 7 = 154 sq.cm.
Also, if we know the circumference of the circle, then we can find the area of circle.How?Since, the circumference is 2 times of product of pi and radius of circle, such as:C = 2rTherefore, here we can find the value of radius,r = C/2Once, we have evaluated the value of radius, we can easily find the area.
Read Also: Glencoe Geometry: Chapter 7 Test Answer Key
Summary Of All The Properties Of A Circle
Here is a summarized list of all the properties we have learned in the article up to this point.
| Important Properties |
Solution
Step 1: Given
- The lengths of two sides other than hypotenuse of a right triangle are 6 cm and 8 cm.
- This triangle is inscribed in a circle.
Step 2: To find
Step 3: Approach and Working out
Let us draw the diagrammatic representation.
- And, once we find the length of the diameter, we can find the radius, and then we can find the area of the circle as well.
Applying Pythagoras theorem in ABC,
- AB² = AC² + BC²
- AB² = 6² + 8² = 36 +64 = 100
- AB = 10 cm
Since AB is the diameter, AB = 2R = 10
- Hence, R = 5 cm.
Area of the circle = × R²= × 5² = 25 .
Hence, the correct answer is option E.
Inscription In Or Circumscription About Other Figures
In every triangle a unique circle, called the incircle, can be inscribed such that it is tangent to each of the three sides of the triangle.
About every triangle a unique circle, called the circumcircle, can be circumscribed such that it goes through each of the triangle’s three vertices.
A tangential polygon, such as a tangential quadrilateral, is any convex polygon within which a circle can be inscribed that is tangent to each side of the polygon. Every regular polygon and every triangle is a tangential polygon.
A cyclic polygon is any convex polygon about which a circle can be circumscribed, passing through each vertex. A well-studied example is the cyclic quadrilateral. Every regular polygon and every triangle is a cyclic polygon. A polygon that is both cyclic and tangential is called a bicentric polygon.
A hypocycloid is a curve that is inscribed in a given circle by tracing a fixed point on a smaller circle that rolls within and tangent to the given circle.
You May Like: Beth Thomas Parents
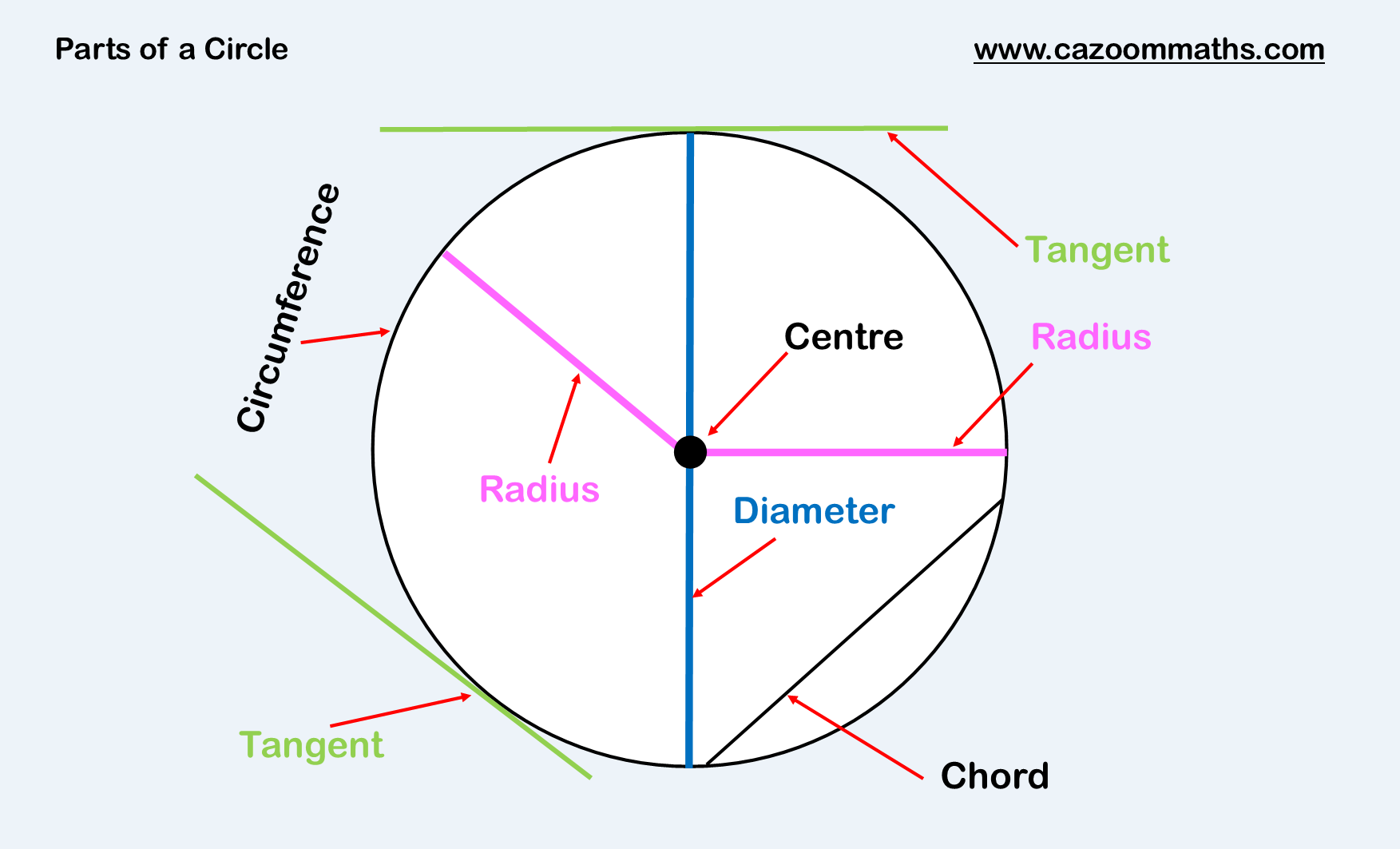
Terminology Related To Circles In Math:
Origin :It is a center point of the circle. Here O is the origin of the circle.
Radius : Distance from center of circle to any point around it circumference is called Radius of the circle.Generally it is denoted by r .
Diameter: The longest distance from one end of a circle to the other end of the circle is called dia of the circle. Generally it is denoted by D . Diameter of the circle = 2 x Radius of the circle. i. e D = 2r.
Arc of a circle: It is a part of the circumference of the circle. The bigger one is called the major arc and the smaller one the minor arc.
Sector of a circle: It is a part of the area of a circle between two radii .
Chord :A line segment within a circle that touches two points on the circle is called chord of a circle.
Circumference : The distance around the circle is called circumference or perimeter of the circle.
Pi : It is a number equal to 3.141592 or 22/7.
The pi = / of any circle.
Tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle.
Secant of circle : A line that intersects a circle at two points then it is called Secant of circle.
Galois Cohomology And Orthogonal Groups
In the theory of of , some further points of view are introduced. They have explanatory value, in particular in relation with the theory of quadratic forms but were for the most part post hoc, as far as the discovery of the phenomena is concerned. The first point is that over a field can be identified as a Galois H1, or twisted forms of an orthogonal group. As an algebraic group, an orthogonal group is in general neither connected nor simply-connected the latter point brings in the spin phenomena, while the former is related to the .
The ‘spin’ name of the spinor norm can be explained by a connection to the . This may now be explained quickly by Galois cohomology . The spin covering of the orthogonal group provides a of .
- 1 1 \rightarrow \mathrm _\rightarrow \mathrm } \rightarrow 1}
Here 2 is the over a field of characteristic not 2 it is roughly the same as a two-element group with trivial Galois action. The from H0, which is simply the group OV of F-valued points, to H1 is essentially the spinor norm, because H1 is isomorphic to the multiplicative group of the field modulo squares.
There is also the connecting homomorphism from H1 of the orthogonal group, to the H2 of the kernel of the spin covering. The cohomology is non-abelian so that this is as far as we can go, at least with the conventional definitions.
Don’t Miss: Unit 1 Test Study Guide Geometry Basics Gina Wilson
Circumference And Area Of A Circle: A Middle School Math Hands
Circles
In Middle School Math, yet again another topic that comes to mind that middle schoolers need to learn and will be tested on is circles, specifically circumference and area. These two concepts can be downright boring if taught by the old chalk and talk method.
But lo and behold, I continually tried to find new and creative ways to teach some of the most mundane and boring math topics. Even before getting to actual activity at hand, I was lucky enough to teach alongside some really fabulous teachers and one can me this idea for how to introduce the two concepts. When thinking of circles, students are first and foremost introduced to a few basic principles.
So what are the words that kids must learn the definitions to before they can even begin to work with circles? Well look no further here they are.
Of Indefinite Quadratic Form Over The Reals
Over the real numbers, are classified by , which asserts that, on a vector space of dimension n, such a form can be written as the difference of a sum of p squares and a sum of q squares, with p + q = n. In other words, there is a basis on which the matrix of the quadratic form is a , with p entries equal to 1, and q entries equal to 1. The pair called the inertia, is an invariant of the quadratic form, in the sense that it does not depend on the way of computing the diagonal matrix.
The orthogonal group of a quadratic form depends only on the inertia, and is thus generally denoted O. Moreover, as a quadratic form and its opposite have the same orthogonal group, one has O = O.
The standard orthogonal group is O = O = O. So, in the remainder of this section, it is supposed that neither p nor q is zero.
The subgroup of the matrices of determinant 1 in O is denoted SO. The group O has four connected components, depending on whether an element preserves orientation on either of the two maximal subspaces where the quadratic form is positive definite or negative definite. The component of the identity, whose elements preserve orientation on both subspaces, is denoted SO+.
The group O is the that is fundamental in . Here the 3 corresponds to space coordinates, and 1 corresponds to the time coordinate.
Don’t Miss: What Is Figure Ground Perception Psychology
Meaning Of Function With Circle And Cross
- 1 copper.hatDec 5 ’12 at 1:36
- $\begingroup$The article calculated hash functions. tmp is a hash value and Pi is a random secret$\endgroup$
In logic and CompSci, $\oplus$ is used to denote the “exclusive or” or “XOR”: $\quad x \lor y \land \lnot$.
In set theory, $\oplus$ denotes the disjoint union.
In linear algebra/vector analysis, it’s used to denote the direct sum of two vector spaces.
It’s also used to denote parity: see P Parity.
Clearly, the context in which it’s used is crucial.
In $LaTeX$: use \oplus.
Properties Related To Angles In A Circle
Inscribed Angle
An inscribed angle is the angle formed between two chords when they meet on the boundary of the circle.
Properties of Inscribed Angles
1. Angles formed by the same arc on the circumference of the circle is always equal.
2. The angle in a semi-circle is always 90°.Central Angle
A central angle is the angle formed when two-line segments meet such that one of the endpoints of both the line segment is at the center and another is at the boundary of the circle.
Property of Central Angles
- An angle formed by an arc at the center is twice the inscribed angle formed by the same arc.
Also Check: Determine The Molecular Geometry Of Each Of The Following Molecules
Centered At Any Location
To find the equation for a circle in the coordinate plane that is not centered at the origin, we use the distance formula. This method can also be used to find the equation for a circle centered at the origin, but in such a case, using the equation in the previous section would be more efficient.
Given a circle with radius, r, centered at point , we can use the distance formula to find that:
where is any point on the circle.
Squaring both sides of the equation, we get the equation of the circle:
2 + 2 = r2
Notice that if the circle is centered at the origin, , then both h and k in the equation above are 0, and the equation reduces to what we got in the previous section:
x2 + y2 = r2
Find the equation of the circle with center and radius 5.
Substituting the coordinates of the center and radius we get,
2 + )2 = 52
2 + 2 = 25