Examples Of Multiple In A Sentence
multiplemultiplemultiplemultiple ofmultiplemultiple USA TODAYmultiple Rolling Stonemultiple Anchorage Daily Newsmultiple BostonGlobe.commultiple The Enquirermultiple EW.commultiple Forbesmultiple CBS Newsmultiple Forbesmultiple The Enquirermultiple Forbesmultiple Health.commultiple WSJmultiple CNNmultiple Dallas Newsmultiple Forbes
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘multiple.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
What Is The Difference Between A Factor And A Multiple
A
Factors are the numbers that are multiplied in order to create a multiple. Multiples are the numbers created by multiplying two factors. Multiples are unlimited, and can be found by simply skip counting. For example, the multiples of \ are \ and so on. However, the factors of \ are limited. The factors of \ are the numbers that multiply to \, such as \, \, and \.
Q
Why Are Factors And Multiples Important
A
Factors and multiples are important in the field of math in many ways. For example, factors and multiples are used when looking for patterns in numbers, simplifying fractions, or when determining the greatest common factor. For example, when simplifying the fraction \, we see that both \ and \ share a common factor of \, so both numbers can be divided by \ in order to simplify the fraction. \ becomes \.
Q
Don’t Miss: Why Is Standardization Important In Chemistry
Multiples And Factors In Ks1 And Ks2
Year 2
- 2
- 5
- and 10 .
Year 3multiples of 2, 5 and 10 up to 1000Year 4multiples of any number up to 10learn about factors in Year 4
- For example: they may be given the number 60 and asked to pick out two pairs of factors from the following numbers: 7, 3, 9, 8, 15, 4, 20.
- They may also need to find common multiples. For example: they may be given the numbers 6 and 9 and asked to find three multiples that have both these numbers as factors.
Year 5square numbersTwo factors of 90 are added together to make another factor of 90. What are the two factors?What am I? I am a multiple of 4. I am between 25 and 50. I am also a multiple of 10.Two square numbers are added together to make a multiple of 9. What could the two square numbers be?lowest common multiplehighest common factor
What Is A Multiple
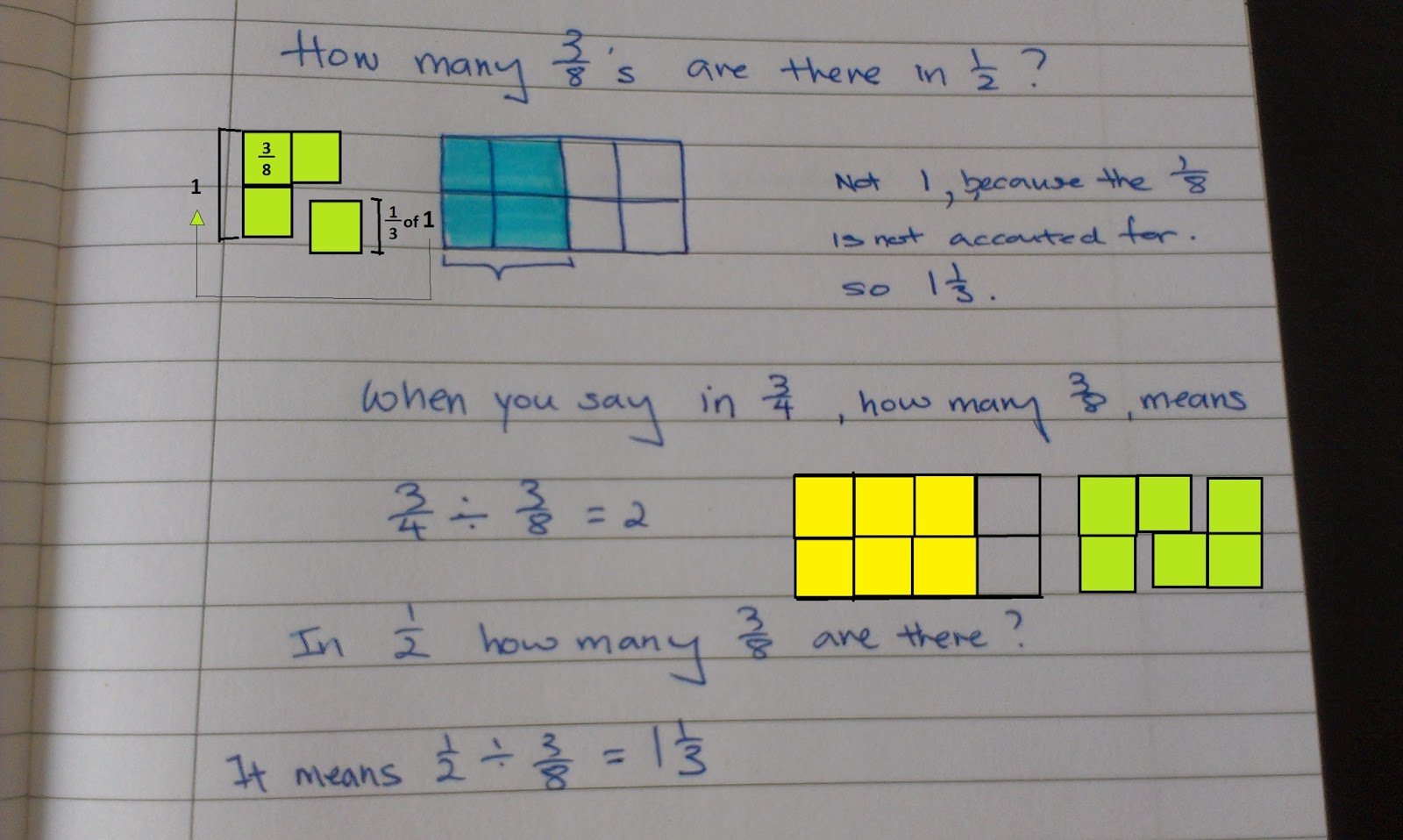
To define it simply, a multiple of a number is the product of that number and another non-zero whole number.For example, 12 is a product of 2 and 6. Both 2 and 6 are non-zero whole numbers.
When you keep finding the product of a number by multiplying it with a series of whole numbers in any numerical order, you will get a multiplication table of that number.
For example:
For this, we are going to continue with the number 7 and make up a multiplication table for it.
| 7 1 = 7 |
| 7 1 0= 70 |
Practice Question #1. Practice the same steps with the number 5.
Here, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70 are all multiples of 7. We stopped the table at 10, but in reality, it can go up to infinity. You did a good job of understanding the basic concept of multiples. Lets add a few rules or properties to make it even easier.
Don’t Miss: Solving Age Word Problems
The Least Common Multiple Is
…the smallest multiple common to all whole numbers in the set.
Problem: An ice cream truck visits Jeannette’s neighborhood every 4 days during the summer. Unfortunately, she missed it today. When can Jeannette expect the ice cream truck to visit her neighborhood again?
Solution: The ice cream truck will visit on days 4, 8, 12, 16, 20, 24, 28, 32, …
In the problem above, we found multiples of the 4. The multiples of a whole number are found by taking the product of any and that whole number. For example, to find the multiples of 3, multiply 3 by 1, 3 by 2, 3 by 3, and so on. To find the multiples of 5, multiply 5 by 1, 5 by 2, 5 by 3, and so on. The multiples are the products of these multiplications. Some examples of multiples can be found below. In each example, the counting numbers 1 through 8 are used. However, the list of multiples for a whole number is endless. The … at the end of each list below lets us know that the list really goes on forever.
| Example 1: |
| Solution: | The multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56,… |
Problem: During the summer months, one ice cream truck visits Jeannette’s neighborhood every 4 days and another ice cream truck visits her neighborhood every 5 days. If both trucks visited today, when is the next time both trucks will visit on the same day?
Truck Days of Visits
1 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44,…
2 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55,…
Solution: LCM = 60
Princeton’s Wordnetrate This Definition:
multipleadjective
the product of a quantity by an integer
“36 is a multiple of 9”
multipleadjective
having or involving or consisting of more than one part or entity or individual
“multiple birth” “multiple ownership” “made multiple copies of the speech” “his multiple achievements in public life” “her multiple personalities” “a pineapple is a multiple fruit”
Read Also: Founding Father Of Behaviorism
Glossary Of Mathematical Symbols
| It has been suggested that List of mathematical symbols by subject be merged into this article. Proposed since January 2021. |
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.
The most basic symbols are the , and the letters of the Latin alphabet. The decimal digits are used for representing numbers through the HinduArabic numeral system. Historically, upper-case letters were used for representing points in geometry, and lower-case letters were used for variables and constants. Letters are used for representing many other sort of mathematical objects. As the number of these sorts has dramatically increased in modern mathematics, the Greek alphabet and some Hebrew letters are also used. In mathematical formulas, the standard typeface is italic type for Latin letters and lower-case Greek letters, and upright type for upper case Greek letters. For having more symbols, other typefaces are also used, mainly boldface a
How To Find Multiples Of A Number
We get the multiples of a number when we multiply the given number by another number. In other words, a multiple is the product that we get when one number is multiplied by another number. For example, if we say 8 × 5 = 40, here 40 is a multiple of 8 and 5. The other multiples of 8 can be listed as 8 , 16 , 24 , and so on.
You May Like: Which Founding Contributors To Psychology Helped Develop Behaviorism
What Is The Definition Of A Factor In Math
A
Factors are the numbers we can multiply together in order to get another number. For example, the factors of \ are \ and \ because these numbers can be multiplied together to get \. \, \, and \. Technically, factors can be negative as well, but in general, when you are listing the factors of a number, you only need to list the positive factors.
Q
What Are Common Multiples
Common multiples of any two numbers are the multiples that are common to both the given numbers. For example, the multiples of 3 can be listed as 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. Similarly, the multiples of 5 can be listed as 5, 10, 15, 20, 25, 30. Now, if we identify the common multiples of 3 and 5 in these two lists, we get 15 and 30.
Recommended Reading: Molecular Geometry Ccl4
Factors Are Not Multiples
Often easily confused, factors are not like multiples at all. Essentially, factors are what we multiply to get a number, and multiple is the result of that multiplication when calculated with an integer.
While there are infinite numbers of multiples, factors are finite. They are also less than or equal to the integer or number, whereas a multiple of a number is always equal or greater than its numbers.
For Example 2×2=4, Here 2 is the factor of 4 and 4 is the multiple of 2.
Answers To The Practice Questions
Practice question 1. The products to multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, when the table stops at 10.
Practice question 2. The LCM of 8 and 10 is 40.
Practice question 3. The LCM of 30 ad 45 is 90.
Practice question 4. The LCM of 20 and 84 is 420
Practice question 5. The product 345 and 28 is 9660.
You May Like: Unit 1 Test Geometry Basics Answers Key
What Are Multiples And Factors
multiplenumber that can be divided by another number a certain number of times without a remainderfactorone of two or more numbers that divides a given number without a remaindernumber sentenceYear 4times tablesmultiples of any number up to 10learn about factors in Year 4
- For example: they may be given the number 60 and asked to pick out two pairs of factors from the following numbers: 7, 3, 9, 8, 15, 4, 20.
- They may also need to find common multiples. For example: they may be given the numbers 6 and 9 and asked to find three multiples that have both these numbers as factors.
Year 5square numbersTwo factors of 90 are added together to make another factor of 90. What are the two factors?What am I? I am a multiple of 4. I am between 25 and 50. I am also a multiple of 10.Two square numbers are added together to make a multiple of 9. What could the two square numbers be?lowest common multiplehighest common factor
Checking Against The Pattern
This pattern doesnt tell us how many stitches are in the stitch repeat, so we need to figure it out by looking at the pattern. The stitches you repeat in Row 1 are sc in next 4 ch, 3 sc in next ch, sc in next 4 ch, skip next 2 ch. These are also the same stitches you repeat in Row 2, except working into single crochet stitches instead of into chain stitches. Adding up the stitches you repeat you end up with 11 sts, but this is not the entire row youre missing some on either end.
At the start of the row you did one sc into a stitch and also skipped a stitch, so you have 2 extra sts at the start of the row.
Lets check this amount against the number of stitches. If we take 156 sts and subtract 2, we get 154 sts. 154 / 11 = 14, so we know 154 is a multiple of 11. This ripple pattern is a multiple of 11 + 2 for the pattern itself. For the foundation chain we will need to add an extra stitch to account for the turning chain.
The multiple of 11 that is closest to 78 is 77, so you will add 77 chains to the beginning chain for a total of 234 chains and 233 stitches.
Recommended Reading: Eoc Fsa Warm Ups Algebra 1 Answers
Chambers 20th Century Dictionaryrate This Definition:
Multiple
multi-pl, adj. having many folds or parts: repeated many times.n. a number or quantity which contains another an exact number of times.n.Multiplepoinding , a process by which a person who has funds claimed by more than one, in order not to have to pay more than once, brings them all into court that one of them may establish his right.Common multiple, a number or quantity that can be divided by each of several others without a remainder Least common multiple, the smallest number that forms a common multiple.
How Can I Make My Crochet Blanket Bigger
Lets take a close look at the Rickrack Rainbow Baby Blanket pattern.
Like the knit blanket example, imagine that you want to make this ripple blanket, but you want it to be about the size of a Twin sized bed comforter . To make the blanket longer, you just continue to crochet until it is the desired length, but in order to make it wide enough, well have to do some math.
As written, this blanket is 36 wide. The pattern has you chain 157 to get 156 sts and it has a gauge of 18 sts = 4 in the ripple pattern. We need to add approximately 18 to the width of the blanket to make it as wide as a Twin comforter . We need to calculate how many stitches to add, depending on the number of stitches in the ripple pattern. 156 stitches divided by 36 inches = 4.33 sts per inch. 4.33 sts x 18 = 78 additional stitches, so well add about 78 stitches. Lets check that against the pattern.
Read Also: Ccl4 Lewis Structure Molecular Geometry
Symbols That Do Not Belong To Formulas
In this section, the symbols that are listed are used as some sorts of punctuation marks in mathematical reasoning, or as abbreviations of English phrases. They are generally not used inside a formula. Some were used in classical logic for indicating the logical dependence between sentences written in plain English. Except for the first two, they are normally not used in printed mathematical texts since, for readability, it is generally recommended to have at least one word between two formulas. However, they are still used on a black board for indicating relationships between formulas.
- ,
- Used for marking the end of a proof and separating it from the current text. The initialismQ.E.D. or QED is often used for the same purpose, either in its upper-case form or in lower case.
- Bourbaki dangerous bend symbol: Sometimes used in the margin to forewarn readers against serious errors, where they risk falling, or to mark a passage that is tricky on a first reading because of an especially subtle argument.
- Abbreviation of “therefore”. Placed between two assertions, it means that the first one implies the second one. For example: “All humans are mortal, and Socrates is a human. Socrates is mortal.”
- Abbreviation of “because” or “since”. Placed between two assertions, it means that the first one is implied by the second one. For example: “11 is prime it has no positive integer factors other than itself and one.”
Examples Of Common Multiple In A Sentence
common multiplesNew York Timescommon multiple Billboardcommon multiple Quanta Magazinecommon multipleWSJ
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘common multiple.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Read Also: Is Paris Michael Jackson Biological Child
How Can I Make My Knit Blanket Bigger
Lets take a close look at the Lace Chevrons Baby Blanket pattern.
The blog example states:
Imagine that you want to make this baby blanket, but you want it to be about the size of a Twin sized bed comforter . To make the blanket longer, you just continue to knit until it is the desired length, but in order to make it wide enough, well have to do a bit of math.
First off, the blanket pattern, as written is 36 wide. It asks you to cast on 156 stitches . This gauge means we need to add approximately 18 to the width of the blanket to make it as wide as a Twin comforter . We will add about 78 stitches DEPENDING UPON the number of stitches in the repeated zigzag chevron pattern. . Now we will refer to the pattern to see how many stitches are in the repeated pattern .
In the Stitch Pattern section, the pattern tells us that it uses an 11 stitch repeat, therefore we will need to add a multiple of 11 to the total of stitches that will be cast on. The closest multiple of 11 to 78 is 77, therefore you will cast on 233 stitches total .
Basic Mathematical Symbols With Name Meaning And Examples
The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.
| Symbol |
|---|
Read Also: Draw The Lewis Structure For Ccl4