Read The Concise Reflection In Geometry Definition
Reflection in Math happens when a figure makes an identical mirrored representation of itself across either the x-axis or y-axis. You can Reflect in Math by changing the sign on the x-values or y-values of the figure. The x-values will change signs when reflecting over the y-axis. The y-values change signs when reflecting over the x-axis. Make sure you label your vertices when drawing your new figure on the coordinate grid.
Graph Functions Using Reflections About The X
Another transformation that can be applied to a function is a reflection over the x or y-axis. A vertical reflection reflects a graph vertically across the x-axis, while a horizontal reflection reflects a graph horizontally across the y-axis. The reflections are shown in Figure 9.
Figure 9. Vertical and horizontal reflections of a function.
Notice that the vertical reflection produces a new graph that is a mirror image of the base or original graph about the x-axis. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the y-axis.
Reflection Over A Horizontal Or Vertical Line
In this video, you will learn how to do a reflection over a horizontal or vertical line, such as a reflection over the line x=-1.
Lets use triangle ABC with points A, B, and C.
Apply a reflection over the line x=-3
Since the line of reflection is no longer the x-axis or the y-axis, we cannot simply negate the x- or y-values. This is a different form of the transformation.
Lets work with point A first. Since it will be a horizontal reflection, where the reflection is over x=-3, we first need to determine the distance of the x-value of point A to the line of reflection. Well be using the absolute value to determine the distance.
Since point A is located three units from the line of reflection, we would find the point three units from the line of reflection from the other side. The y-value will not be changing, so the coordinate point for point A would be
Repeat for;points B and C. In the end, we found out that after a reflection over the line x=-3, the coordinate points of the image are:
A’, B’, and C’
You May Like: How Did Geography And Religion Influence Ethiopia’s Development
A General Note: Reflections
Given a function f\left\\, a new function g\left=-f\left\\ is a vertical reflection of the function f\left\\, sometimes called a reflection about the x-axis.
Given a function f\left\\, a new function g\left=f\left\\ is a horizontal reflection of the function f\left\\, sometimes called a reflection about the y-axis.
What Are The Rules For Reflections Heres Everything You Need To Know
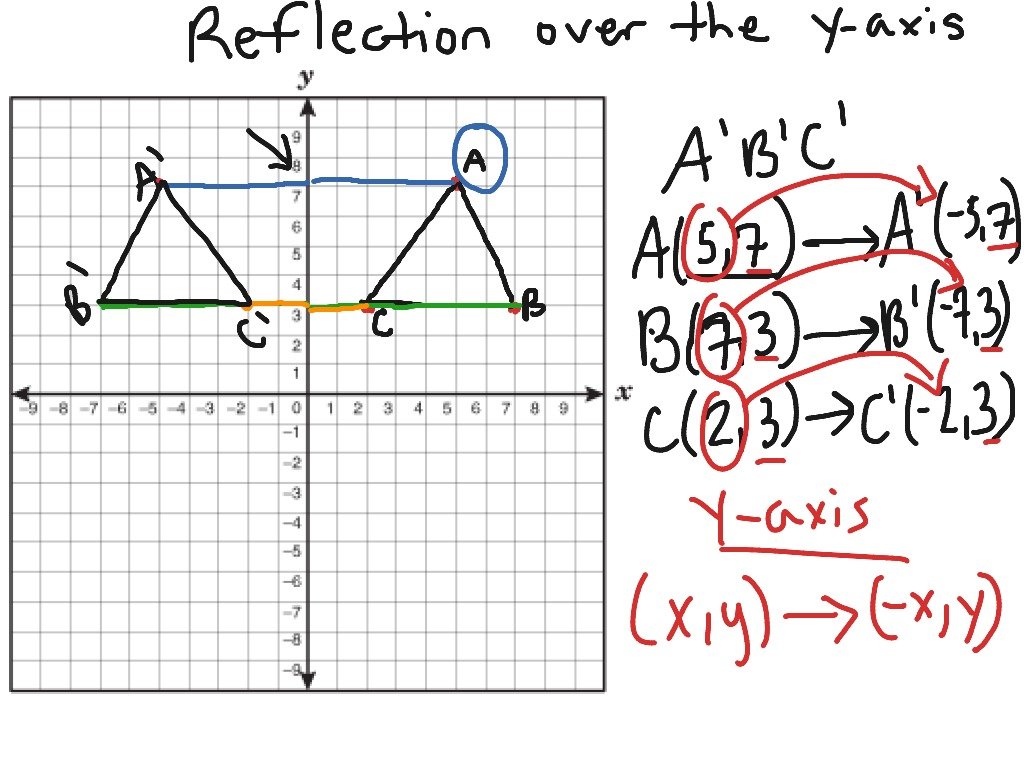
Reflection on a Coordinate Grid involves flipping figures on a coordinate grid. Reflection in Math takes place when a figure makes a mirror image of itself. Reflection in Math usually of a figure takes place over either the x-axis or the y-axis. You can Reflect on a Coordinate Grid by changing the sign on the x or y coordinates depending on which axis you reflect over. If you reflect over the x-axis, all the signs on the y-values in the coordinates will change. If you reflect over the y-axis, all the signs on the x-values in the coordinates will change. The last step for Reflections on a Coordinate Grid is to write the coordinates of the new location of the figure.
Common Core Standard: 8.G.4
You May Like: Bridge To Algebra 2nd Ed Answers
Reflections Over The Y
Now, reflections over the y-axis, same thing really. If we reflect a point over the y-axis, the original point and the reflected image have the same y-coordinate. They lie on the same horizontal line, so here are two points on the same horizontal line. The x-coordinates have equal absolute values and opposite positive or negative signs.
So, if we have a negative x value it becomes positive, if we have a positive x value it becomes negative. So in each case the two points are reflections of each other. is a reflection of , and is a reflection of .
What Is A Reflection In Geometry
A reflection in geometry is a mirror image of a function or object over a given line in the plane. The most frequently used lines are the y-axis, the x-axis, and the line $y=x$, though any straight line will technically work.
A reflection reverses the objects orientation relative to the given line. The final figure will be an equal distance from the line as the preimage but on the opposite side. If the original figure is close to the line, the reflected figure will also be close to the line. If the original figure is further from the line, the reflected figure will also be further from the line.
Put another way, the midpoint between any two corresponding points in the original image and the reflected image lies on the line of reflection.
To visualize the reflected version of an object, imagine a cut-out of the object sitting on a table. If you pick up the original and flip it over onto the backside while moving it over the given line, you will have the reflected versions orientation.
Read Also: What Does Scale Drawing Mean In Math
Video Lesson & Examples
- How to find the line of reflection
- 00:17:45 Graph the given reflection in the coordinate plane
- 00:25:02 Determine the number of lines of symmetry
- 00:30:22 Determine how a square piece of paper will look once unfolded
- 00:35:42 Glide Reflections and the Composition Theorem
- 00:44:53 Overview of how we can Optimize with Geometry
- 00:52:16 Finding the minimum distance using reflections
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
What Is A Reflection In Math
Learning how to perform a reflection of a point, a line, or a figure across the x axis or across the y axis is an important skill that every geometry math student must learn.
In real life, we think of a reflection as a mirror image, like when we look at own reflection in the mirror.
This idea of reflection correlating with a mirror image is similar in math.
This complete guide to reflecting over the x axis and reflecting over the y axis will provide a step-by-step tutorial on how to perform these translations.
;First, lets start with a reflection geometry definition:
Read Also: What Does Algebra 2 Look Like
What Is The Rule For A Reflection Across The Y Axis
The rule for reflecting over the Y axis is to negate the value of the x-coordinate of each point, but leave the -value the same.
For example, when point P with coordinates is reflecting across the Y axis and mapped onto point P, the coordinates of P are . Notice that the y-coordinate for both points did not change, but the value of the x-coordinate changed from 5 to -5.
You can think of reflections as a flip over a designated line of reflection. You can often visualize what a reflection over the x axis or a reflection over the y axis may look like before you ever apply any rules of plot any points. This aspect of reflections is helpful because you can often tell if your transformation is correct based on how it looks. If the new image resembles a mirror image of the original, youre in good shape! If it does not, you probably did something wrong.
The Line Of Reflection
Any line can be a line of reflection, but the axes and the line through the origin with slope 1 are most common.
Note that we can use more than one line in a series of reflections. For example, you can reflect an object over the x-axis and then the y-axis.
What happens when an object passes through the given line?
In that case, the two sides of the object are treated separately. Reflect the part on the right to the left of the line, and then reflect the part on the left of the line onto the right side.
Any function that passes through the y-axis and maps to itself when reflected over the y-axis is an even function. Put another way, even functions are symmetric about the y-axis.
If a function that passes through the origin maps onto itself after being reflected over the y-axis and the x-axis, it is an odd function.
Don’t Miss: Geometry Lesson 1.7 Answers
Easy Steps To Complete Any Reflection Transformation Example
Drawing The Image On Grid Lines
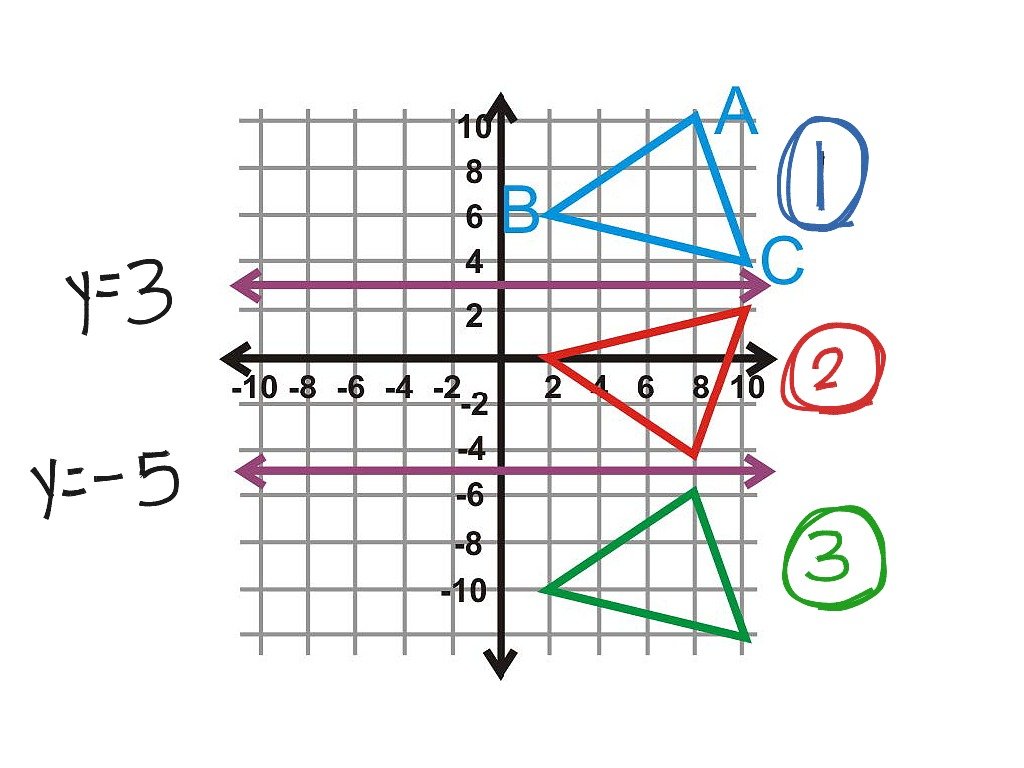
If the axis of reflection is on one of the grid lines, we just count the number of squaresfrom a point on the object to the axis and the image is the same distance from the axis.
Example:In the diagram, the figure A is reflected in the line XY. Draw the image of A in the diagram.
Solution:
Note that the point O remained unchanged under reflection because it is on the axis of reflection.Any point on the line of reflection is unchanged such points are described as invariant.
How to reflect a shape on squared paper without using tracing paperThis video shows how to reflect a shape on squared paper without using tracing paper. Justcount the distance of each corner to the mirror line and count the same distance away fromthe mirror line. Once all the points have been reflected them, join the points up neatlyusing your ruler.
Read Also: How Do You Find Displacement In Physics
Reflection Across The Y
The y-axis, or primary vertical line in the coordinate plane, often acts as a line of reflection in math. Properties of reflection regarding shapes transformed over the y-axis operate in a manner similar to that of shapes transformed over the x-axis. If points reflect across the y-axis, their y-coordinates remain unchanged but their x-coordinates change into their opposites. For instance, when reflected across the y-axis, the point becomes .
Distance To Point Of Reflection
The from the to the point of reflection is equal to the from the point of reflection to the .
A graph showing a triangle’s shape reflected over the origin. The from each vertex of the to the origin is equal to between the origin and each point of the .
The origin might be the most common point of reflection, but you can use any point. And the same rules apply. The diagram below uses the point $$$$ as the point of reflection.
Practice problems like example 5 here.
Don’t Miss: What Is Z In Chemistry
Glide Reflections And Congruence
A glide reflection is the composition of a reflection, and a translation in a vector parallel to the line of reflection. This image gets the idea across:
And here is an interactive figure:
the GeoGebra file.
Of all the possible compositions of isometries, it may seem like a completely arbitrary choice. For example, why not give a special name to the composition of a reflection and a rotation? or a reflection and a translation whose vector is perpendicular to the line of reflection? I am glad you ask these questions. I offer three arguments for the unique significance of the glide reflection:
#2 is truly a fundamental and phenomenal theorem. Think about it: in the CCSSM, two figures are deemed congruent if one is the image of the other in “a sequence of rotations, reflections, and translations”. What this theorem tells us is that if there is such a sequence, then it is equal to a single rotation, reflection, translation, or glide reflection.
Reflection About The Line Y=x
Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection -transformation of a figure.
For example, if we are going to make reflection transformation of the point about x-axis, after transformation, the point would be . Here the rule we have applied is ——> .;
So we get ——-> .
Let us consider the following example to have better understanding of reflection.
Question :
Let A , B and be the three vertices of a triangle. If this triangle is reflected about x-axis, what will be the new vertices A’ , B’ and C’ ?
Solution :
Step 1 :
First we have to know the correct rule that we have to apply in this problem.
Step 2 :
Here triangle is reflected about x – axis. So the rule that we have to apply here is ——->
Step 3 :
Based on the rule given in step 1, we have to find the vertices of the reflected triangle A’B’C’.
Step 4 :
Vertices of the reflected triangle are
A’ , B and C’;;
Also Check: Where’s My Water Cool Math Games
Other Lines Of Reflection
Other lines of reflection are more complicated. This is a situation where construction with a compass and ruler helps in coordinate geometry.
First, create a line from each key point in the figure that meets the reflection line at a right angle. Then, extend this line so that the intersection point with the line of reflection is the midpoint. The other endpoint of this line is the corresponding point in the reflection.
Example 4 covers this in greater detail.
Reflections Across The Line Y = X
A reflection across the line y = x switches the x and y-coordinates of all the points in a figure such that becomes .
Triangle ABC is reflected across the line y = x to form triangle DEF. Triangle ABC has vertices A , B and C . Triangle DEF has vertices D , E , and F . All of the points on triangle ABC undergo the same change to form DEF.
Read Also: Where Do The Biological Products Come From
What Is The Rule For A Reflection Across The X Axis
The rule for reflecting over the X axis is to negate the value of the y-coordinate of each point, but leave the x-value the same.
For example, when point P with coordinates is reflecting across the X axis and mapped onto point P, the coordinates of P are . Notice that the x-coordinate for both points did not change, but the value of the y-coordinate changed from 4 to -4.
Reflecting Over Any Line
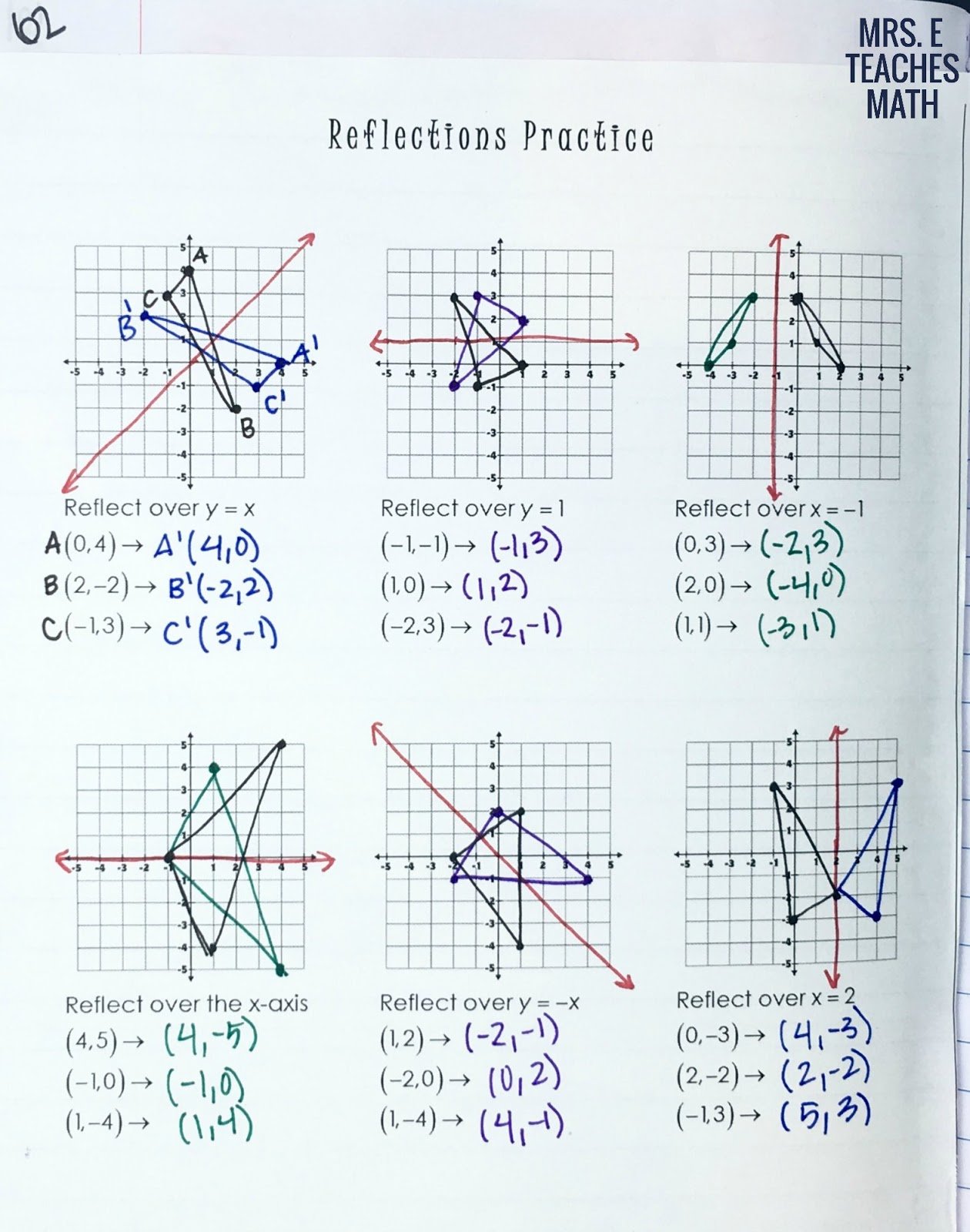
When we look at the above figure, it is very clear that each point of a reflected image A’B’C’ is at the same distance from the line of reflection as the corresponding point of the original figure.;
In other words, the line x = -2 lies directly in the middle between the original figure and its image.
And also, the line x = -2 is the perpendicular bisector of the segment joining any point to its image.;
Students can keep this idea in mind when they are working with lines of reflections which are neither the x-axis nor the y-axis.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.;
If you have any feedback about our math content, please mail us :;
We always appreciate your feedback.;
You can also visit the following web pages on different stuff in math.;
|
ALGEBRA |
Recommended Reading: What Does Kw Mean In Chemistry
What Makes Good Reflective Writing
Academic reflective writing requires critical and analytic thought, a clear line of argument, and the use of evidence through examples of personal experiences and thoughts and often also theoretical literature. You should aim for a balance between personal experience, tone, and academic practice and rigor.
Reflections Across Y = X And Y =
The lines y = x and y = -x are the two primary diagonal lines of the coordinate plane and the most common diagonal lines over which points and shapes are reflected. In a reflection over the line y = x, the x- and y-coordinates simply switch positions. For example, suppose the point is reflected over y = x. The coordinates of the reflected point are . Likewise, reflections across y = -x entail reversing the order of the coordinates, but also switching their signs. For example, turns into when reflected over the line y = -x.
References
Recommended Reading: What Is The Importance Of Biology In Our Daily Life
How Do You Describe A Reflection In Math
How do you describe a reflection in math? In geometry, a reflection is a type of rigid transformation in which the preimage is flipped across a line of reflection to create the image. Each point of the image is the same distance from the line as the preimage is, just on the opposite side of the line.
How do you describe a reflection?;A reflection is a transformation that acts like a mirror: It swaps all pairs of points that are on exactly opposite sides of the line of reflection. The line of reflection can be defined by an equation or by two points it passes through.
How do you write a reflection in math?;In a reflection over the line y = x, the x- and y-coordinates simply switch positions. For example, suppose the point is reflected over y = x. The coordinates of the reflected point are . Likewise, reflections across y = -x entail reversing the order of the coordinates, but also switching their signs.
What is another way to describe a reflection in math?;reflection a transformation in which the direction of one axis is reversed. Synonyms: mirror image, expression, reflexion, reflectivity, manifestation, contemplation, thoughtfulness, rumination, observation, musing. A flip is also called a reflection. Another name for reflection symmetry.