What Does Parallel Mean In Math

Who Else Wants To Learn About What Does Parallel Mean In Math

On the flip side, house prices could be higher than they should be attributed to local policies that needlessly drive up the amount of land and thereby constrain the quantity of new housing. It may be a Known Issue. This example illustrates the issue.

Following that, all the rest of the blanks are primes. Ensure you fully grasp all the significant attributes and formulas related to shapes, particularly circles and triangles. Example If we take a look at the rectangle below, we can observe it has twice the region of the blue triangle inside it as the two yellow triangles are the exact same size as the two sub-divided blue triangles.

What Do Parallel Lines Look Like

In the figure below, line AB is parallel to the line CD.

The perpendicular distance is always the same between two parallel lines.

Sides of various shapes are parallel to each other. In the rectangle given below, the single arrow lines are parallel to each other, and similarly, the double arrow lines are also parallel to each other.

Parallel lines are represented with a pair of vertical lines between the names of the lines, using the sign:

Draw parallel lines on a sheet,

Use a ruler to make them neat!

Make sure their ends never meet!

How To Modify A Bentley Map Feature In Microstation

• Ability to modify a Bentley Map feature in MicroStation Attempting to align text with horizontal line using “align element by edge” tool Convert automatically Linestring to Complex polygonal shape Converting various elements to one elevation. Copying element from reference with Level Lock On does not copy any Elements

Recommended Reading: How To Solve Normality Problems In Chemistry

What Does It Mean For Two Things To Be Parallel

In math, parallel means two lines that never intersect think of an equal sign. Figuratively, parallel means similar, or happening at the same time.

What is a good example of parallelism?

In English grammar, parallelism is the repetition of the same grammatical form in two or more parts of a sentence. I like to jog, bake, paint, and watching movies. I like to jog, bake, paint, and watch movies.

Applications Of Parallel Lines In Real

Parallel lines can easily be observed in real-life. One of the best examples of parallel lines is the railway tracks. These tracks are literally parallel lines in real life, as they are supposed to be always parallel to each other to grip the wheels of the train at all costs. Some other real-life examples of parallel lines are the edges of an almirah, scale , etc.

Also Check: What Is Duplication In Biology

Real Life Examples Of Parallel Lines

• Yard marks on a football field are parallel lines

• Edges of a ruler are parallel lines

• Opposite sides of many picture frames are parallel lines

• Railway track are parallel lines

• Edges of many computer screens are parallel lines

Would you prefer to share this page with others by linking to it?

Why Do Parallel Lines Never Meet

Parallel & Intersecting lines Two lines in the same plane will always intersect unless they are parallel. Parallel lines are lines that are always the same distance apart and they never intersect. … The rails on a railroad track are always the same distance apart,they run in the same direction, and they never intersect.

Don’t Miss: Geometry Dash 1.1 Apk

Traversals Of Parallel Lines

In this figure, a transversal (line P

. \lvert\overline\rvert=\lvert\overline\rvert. PQ=PQ. This implies that two parallel lines are always a constant distance apart from each other, which is another important characteristic of parallel lines.

Thinking more intuitively, this has to be true since if the lines were getting farther apart from each other, then on the opposite side of the lines would be getting closer , which contradicts the definition that two parallel lines never meet. Note that the distance between two distinct lines can only be defined when the lines are parallel. If the lines are not parallel, then the distance will keep on changing.

The discussion just above, for your information, in fact accords to Euclid’s fifth postulate, or the parallel postulate. It states that if a line segment intersects two straight lines forming two interior angles on the same side that sum to less than 180 degrees, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than 180 degrees. In other words, two lines are parallel when the interior angles on the same side sum to exactly 180 degrees.

In summary,

What Does It Mean To See A Parallel

If something has a parallel, it is similar to something else, but exists or happens in a different place or at a different time. If one thing parallels another, they happen at the same time or are similar, and often seem to be connected. Often there are emotional reasons paralleling the financial ones.

What does it mean when something has a parallel?

If something has a parallel, it is similar to something else, but exists or happens in a different place or at a different time. If it has no parallel or is without parallel, it is not similar to anything else.

Don’t Miss: What Is Systems Theory In Psychology

Slope Of Parallel Lines

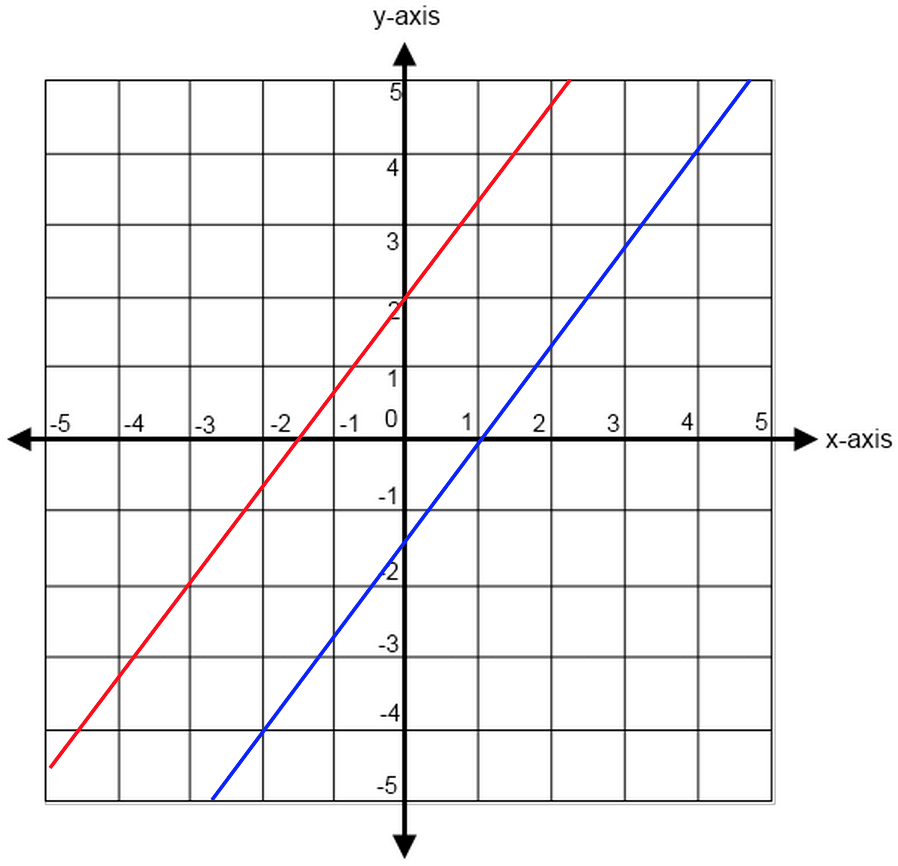
In coordinate geometry, parallel lines have the same slope. The converse is also true if two lines have the same slope, the two lines are parallel unless they overlap.

The blue line below is the graph of the equation y = 2x + 3 and the black line is y = 2x – 4. The slope for both lines is, m = 2. Two vertical lines are still parallel even though their slopes are undefined.

Knowing that two lines are parallel is useful for finding the equation of a line even when given little information about it.

Example:

Suppose a line contains the point and is parallel to the line that has an equation of y = 2x + 6.

The slope of the given line is 2.

Using the point-slope formula, we have,

Slope Of Perpendicular Lines

Suppose two lines AB and CD are perpendicular to each other. The slope of line AB is m1 and the slope of other line CD is m2.

Statement: Two lines are perpendicular to each other if and only if the product of the slope of the two lines equals minus of unity.

Thus, the formula for the slope of the perpendicular is given as:

In the case of the parallel line, the slope of the two lines is parallel to each other.

m1 = m2

Read Also: How Does Double Glazing Work Physics

Parallel Lines And Slopes

Parallel lines are lines that do not intersect. In two dimensions, parallel lines have the same .

We can write the equation of a line parallel to a given line if we know a point on the line and an equation of the given line.

Example:

Write the equation of a line that passes through the point ( and is parallel to the line

Parallel lines have the same slope.

The slope of the line with equation y . So, any line parallel to y

Now use the to find the equation.

We have to find the equation of the line which has slope 2 and passes through the point (

is parallel to the line y and passes through the point (

Proving Lines Are Parallel

In a polygon, you can test for parallel sides by checking the notation , by measuring between the two questioned lines, or by applying proofs of parallel lines from Euclid.

If you choose to measure the distance between two sides, make sure measure along a line perpendicular to the two sides, not at an angle. Measuring the angled ends of a trapezoid, for example, will not provide definite proof that the two bases are parallel, because the two ends could be at different angles.

How can we prove lines are parallel? Euclid’s rigor is also helpful since you can prove parallel lines using any of these methods:

You May Like: What Does Point Mean In Geometry

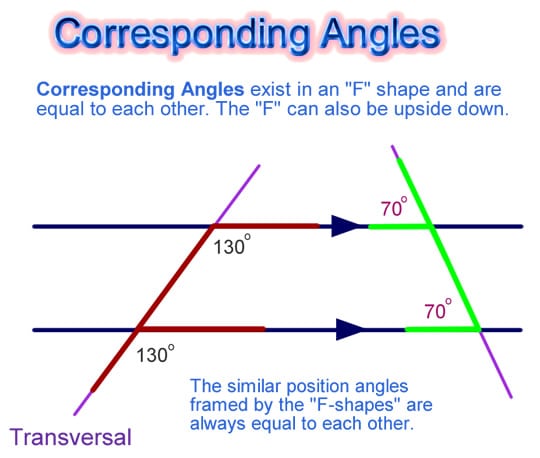
Transversals Of Parallel Lines And Their Angles

When 2 lines are cut by a third line, called a transversal, 8 angles are formed.

Parallel lines m and n are cut by transversal l, above, forming angles 18.

• 1, 2, 7, 8 are called exterior angles.
• 3, 4, 5, 6 are called interior angles.
• 1 and 5, 2 and 6, 3 and 7, 4 and 8 are called corresponding angles.
• 3 and 6, 4 and 5 are pairs of consecutive interior angles.
• 1 and 8, 2 and 7 are pairs of exterior angles on the same side of the transversal.

Several relationships exist among these angles.

• Alternating exterior angles are congruent. So, 17 and 28.
• Alternate interior angles are congruent. So, 35 and 46.
• Corresponding angles on the same side of the transversal are congruent. So, 15, 26, 37, and 48.
• Consecutive interior angles are supplementary. So, 3 + 6 = 180° and 4 + 5 = 180°.
• Exterior angles on the same side of the transversal are supplementary. So, 1 + 8 = 180° and 2 + 7 = 180°

In summary, 1, 3, 5, 7 are congruent and2, 4, 6, 8 are also congruent. 1, 3, 5, 7 are supplementary to 2, 4, 6, 8, respectively.

If any of the eight angles formed by two parallel lines and a transversal is a right angle, all the angles formed are right angles and the transversal is perpendicular to the two parallel lines.

What Does Parallel Mean In Math Secrets That No One Else Knows About

Two parameters will be utilised to figure out the number. The 2 middle numbers only will need to get averaged while the data set has an even number of information points in it. It is also feasible to have a whole set of data without a mode.

A set of data values collected by means of a survey or experiment is called a sample. If so make certain you measure performance for your data to choose if you ought to use above law coursework writing service uk code VS just straight sorting. Factor analysis is a sort of exploratory multivariate analysis thats used to either decrease the variety of variables in a model or maybe to detect relationships among variables.

A square is a normal quadrilateral. In the majority of cases, you can discover specific solutions to your equations. Go right ahead and plug that into the original equation and see whether it works.

Note you do not need to lower a fraction. The RANGE is just the difference between the biggest and the smallest value. It is crucial to know the three sorts of averages, and once it is suitable to use each one.

These videos will explain to you how to get the median. Much like with royalessays.co.uk/ our examples sets of 3 and 5, we dont need to get an average. The mean of these distribution is 26.

You May Like: What Are The Tools Of Geography

What Does Parallel Lines Mean Definition And Examples

What does parallel lines mean? Parallel lines are lines in the same plane that do not meet or intersect. The following figure shows four lines that are parallel.

Notice that the plane is shown in blue and the four lines that are parallel are shown with green lines. It is important that the lines are located in the same plane as shown above if they will be parallel or not.

What Are Parallel Lines And Perpendicular Lines

Parallel lines are those lines that are equidistant from each other and never meet, no matter how much they may be extended in either directions. For example, the opposite sides of a rectangle represent parallel lines. On the other hand, if any two lines intersect each other at 90°, they are called perpendicular lines. For example, the adjacent sides of a rectangle are perpendicular lines because they intersect each other at 90°.

You May Like: What Does Abiotic Mean In Biology

Parallel Lines Axioms And Theorems

Below are the axioms and theorems of parallel lines:

Corresponding Angle Axiom: Corresponding angles are equal to each other. In corresponding angles axioms, it is said that if the reverse of the property is true, that is, if the reason of the property is true, the assertion must be true as well. The corresponding angles axiom states that if the corresponding angles are equal, it means that the lines on which the transversal is drawn are parallel to each other.

Theorem 1: If a transversal is drawn on two parallel lines, the vertically opposite angles will be equal. From the figure given below:

Therefore, 3 = 5.

Similarly, 4 = 6.

The converse of the theorem is also true that is, if the vertically opposite angles are equal to each other, the lines are parallel in nature.

Theorem 2: If two lines are parallel to each other and are intersected by a transversal, the interior angles pairs are supplementary to each other.

To prove: 4 + 5 = 180° and 3 + 6 = 180°.

Proof: 4 = 6

6 + 5 = 180°

Therefore, 4 + 5 = 180°

Similarly, 3 + 6 = 180°.

The converse of the theorem is also true that is, if the interior angles are supplementary to each other, the lines are parallel in nature.

Construction Of Perpendicular Lines

Construction of the perpendicular line is a very simple process. The angle between the two lines should be equal to 90 degrees. So to construct perpendicular lines, you will need a compass and a straight line ruler or scale. Follow the below steps to draw it:

• Draw a horizontal line first.
• With the help of a compass draw an arc at the center of the line say point O, such that it intersects the line at two points and at equidistant from O. Let the two points be P and Q.
• Again at point P and Q, draw the arc inside, such that the two arcs intersect each other at the top and bottom of the horizontal line.
• Now join the two-point where the two arcs intersect each other.
• Now, the line obtained is perpendicular to the horizontal line.

Also, read:

m1 = /-1 = -3/-1 = 3

m2 = / = 2/ = –

Since, m1 m2, therefore, lines are not parallel.

m1.m2 = 3 x = -1

Therefore, the two lines are perpendicular.

Example 2:

What is the equation for the line that is perpendicular to 4x3y=6 through point ?

Solution:

As we know, the slope of perpendicular lines are opposite reciprocals.

Given, 4x3y=6

Writing in slope-intercept form, we get

y = x 2

So, slope of the line 4x3y=6, m = 4/3

Now, the slope of line perpendicular to the given line is .

Using the coordinates of the point and putting the given equation, we get

6 = + b

Therefore, the required equation of a perpendicular line is given by:

y = x + 9

Read Also: What Is Stimulus Discrimination In Psychology

What Does Parallel Mean In Math The Conspiracy

Unfortunately, in addition, there are some tricky circumstances that require additional notion to specify the range working with the rules alone. Lets look at a few examples. You cant alter this choice after its been made!

While scientists are looking for these clues, others want to get more indirect indications. This writing company makes sure their papers are all the amazing quality and all the customers are pleased. Excellent luck recruiting for this study!

What Is A Perpendicular Line

The perpendicular lines are two lines that intersect each other and the angle formed between the two lines should be equal to 90 degrees . Consider the above-given figure, the line PQ and RS forms a right angle when the lines intersect at a point. Hence, the lines are perpendicular to each other and mathematically it is represented as PQ RS.

When a line is perpendicular to the plane, then it is said to be perpendicular to all the points in the plane or perpendicular to each line in the plane that it intersects. Two planes are said to be perpendicular in space if the dihedral angle at which they meet the plane is a right angle.

Note: Perpendicular lines always intersect at 90 degrees but not all intersecting lines are perpendicular.

Also, read: Intersecting and Non-intersecting Lines

Read Also: Who Is Generally Recognized As The Founder Of American Psychology

Angles In Parallel Lines

An introduction to alternate, corresponding and co-interior angles in parallel lines

Parallel lines are lines which are always the same distance apart and never meet. Arrowheads show lines are parallel.

When a pair of parallel lines is cut with another line known as an intersecting transversal, it creates pairs of angles with special properties.

Spherical Or Elliptic Geometry

Spherical geometryElliptic geometrysphereagreat circlecaba

In spherical geometry, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres and all great circles intersect each other. Thus, there are no parallel geodesics to a given geodesic, as all geodesics intersect. Equidistant curves on the sphere are called parallels of latitude analogous to the latitude lines on a globe. Parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center of the sphere.

If l, m, n are three distinct lines, then l .

In this case, parallelism is a transitive relation. However, in case l = n, the superimposed lines are not considered parallel in Euclidean geometry. The binary relation between parallel lines is evidently a symmetric relation. According to Euclid’s tenets, parallelism is not a reflexive relation and thus fails to be an equivalence relation. Nevertheless, in affine geometry a pencil of parallel lines is taken as an equivalence class in the set of lines where parallelism is an equivalence relation.

Don’t Miss: Big Ideas Math Geometry 4.5 Answers