What Does Point Mean In Geometry

What Is The Exact Difficulty In Defining A Point In Euclidean Geometry

In Euclidean geometry texts, it is always mentioned that point is undefined, it can only be described. Consider the following definition: “A point is a mathematical object with no shape and size.” I do not understand what is the problem with this definition. Please give the detailed reasons. Thanks in advance!

• 29Aug 9 ’16 at 10:56
• 3$\begingroup$If the underlying set is interpreted as a “space” then one calls its elements points.$\endgroup$Aug 9 ’16 at 10:57
• 13$\begingroup$There is no problem with this *statement”. But the issue is to take it as a definition. I we are together out in a nice day and I way “the sky is blue and we can see the moon”, there is no problem, you will say “yes”. But this does not constitute a definition of the sky.$\endgroup$Aug 9 ’16 at 11:21
• 28$\begingroup$There isn’t difficultly in defining a point. Rather, there is flexibility in not-defining a point. This is a feature of geometry, not a bug.$\endgroup$

The exact difficulty is that in mathematics, we define things in termsof other things. We also avoid circular definitions, in other words wedo not want to define $A$ in terms of $B$ where $B$ is defined in terms of $C$ and $C$ is defined in terms of $A$.

In short, in order to build a mathematical theory we have to start withsome “primitive notions” that we will never define. Everything elsecan be defined in terms of those notions.

Under your definition, the following things are points:

I’m sure you agree that none of these things are points.

Examples Of Geometry In A Sentence

geometrygeometry San Antonio Express-NewsgeometryScientific Americangeometry Quanta Magazinegeometry Scientific AmericanQuanta MagazinegeometryDetroit Free Pressgeometry New York Timesgeometry Forbes

These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘geometry.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

What Happens If The Discriminant Is Greater Than 0

When the discriminant is greater than 0, there are two distinct real roots. When the discriminant is equal to 0, there is exactly one real root. When the discriminant is less than zero, there are no real roots, but there are exactly two distinct imaginary roots. In this case, there is exactly one real root.

Don’t Miss: Geometry Dash Practice Music

Points Lines & Planes Lesson & Examples

38 min

• Introduction to points, lines and planes
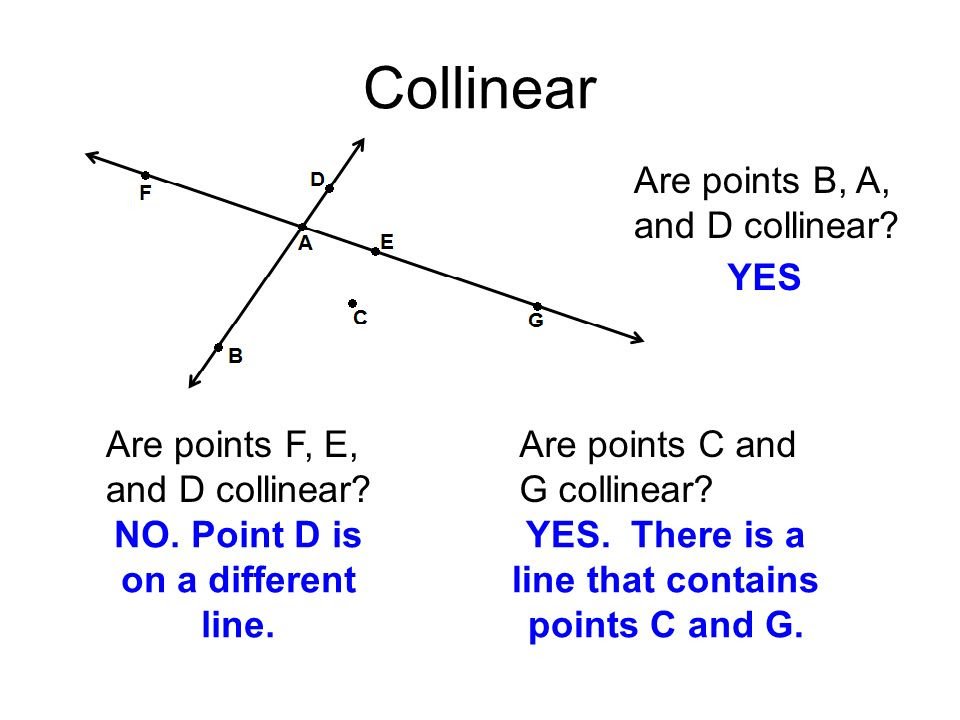
• 00:00:24 Defining terms: Point, Line, Plane, Collinear, and Coplanar
• 00:08:40

• True or false given the diagram of two planes
• 00:18:57 True or false about collinear and coplanar theory
• 00:21:49 Term Definitions: Line Segments and Rays
• 00:27:33 Name the segments or rays given the illustration
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

What Is A Point And A Line

The concept of points and lines is important to understand geometry figures. With the help of points, we can label and identify the geometry figures and with the help of lines, we can draw the figures.

Point

A point is defined as a location in any space and is represented by a dot . It does not have any length, height, shape, or size. It marks the beginning to draw any figure or shape and is labeled with capital letters.

Line

A series of points connected by a straight path is defined as a line. A line is usually defined by two points. It can be marked with a single letter in the lower case or by two capital letters. A line has no thickness and can extend indefinitely in both directions. The length of a line is undefined and it can have infinite numbers of points. Observe the following figure to know the difference between a point and a line.

Don’t Miss: Unit Test Algebra 1

Complete Rejection Of The False Grammatical Account: Geometric Points Are Not Names Of Objects

But the word ‘point’ is not used in geometry to name anything. A point is not a “geometric object” it is not an “atomic dot”. There are no objects in geometry. A point is a location a ‘geometric point’ is a point of reference. That is the grammar of the word.

A point is a location in space. Or in plane geometry: a point is a location in the plane. That is the best general definition of the word ‘point’ as it is used in geometry that I can think of: However, that definition is not by itself for it does not specify everything it should.

A point is an address. In Euclidean geometry, “a point is a relation” — a relation to what? To other points in the plane. That is, when we say that ‘point’ = ‘an address in the plane’, that address look like this: ABC — i.e. the address of point B is given relative to points A and C. It is possible to begin a proof: “Let A be a point of line n”, because that too states a relationship .

By the word ‘point’ we mean ‘a unique location in the plane’. How is that location determined? Relative to other locations. Is that circular? Only in the sense that every system of assigning addresses begins with an arbitrarily assigned point of reference — and there must be other points in the system.

Question: What Is Discriminant In Math Example

Discriminant, in mathematics, a parameter of an object or system calculated as an aid to its classification or solution. In the case of a quadratic equation ax2 + bx + c = 0, the discriminant is b2 4ac for a cubic equation x3 + ax2 + bx + c = 0, the discriminant is a2b2 + 18abc 4b3 4a3c 27c2.

You May Like: Finding Percent Error In Chemistry

What Is A Point

In geometry, what is a point?I have seen Euclid’s definition and definitions in some text books. Nowhere have I found a complete notion. And then I made a definition out from everything that I know regarding maths. Now, I need to know what I know is correct or not.One book said, if we make a dot on a paper, it is a model for a point.Another said it has no size. Another said, everybody knows what it is.Another said, if placed one after another makes a straight line.Another said, dimensionless.Another said, can not be seen by any means.

• 14$\begingroup$A point is undefined almost always in geometry – it is considered an axiomatic object, like a natural number. You can explain what you want a point to represent, but what it “is” is an abstract concept with no definition other than the properties we assert for it in our axioms.$\endgroup$Jan 25 ’13 at 19:19
• 2Jan 25 ’13 at 19:20
• 12Jan 25 ’13 at 19:36

Point, in Euclidean geometry, is an undefined notion.

We do not define what a point is, only what properties points must have, and these properties are completely specified by the axioms. This is certainly a modern view of mathematics, and differs from the approach in Euclid’s times. Euclid defines point, but the definition is vague, and it is never used anyway.

size-less : Any point is too small to exist physically, we mean this when we say that any point is size-less.

constructed by the human-brain : constructed in the mind

Points Lines And Shapes

Definitionof points, lines and shapes in geometry:

Point: A point is the fundamental element of geometry. If we put the tip of a pencil on a paper and press it lightly, we see a very small mark on the paper. This mark is known as a point.

The smallest mark denotes the existence of a point. We say that a point does not have any length, breadth or thickness, but it has a definite position.

It can be named by a capital letter of the English alphabet like A, B, C, . etc.

In short, we can make a small dot on a paper by using a sharp pencilor a tip of the needle. It is called a point. It represents a position and ismarked by a capital letter A, B, C etc. A point has no size or shape. So, on aline an infinite number of points exist.

Line: If two pointsare made at a distance on a surface and are joined by a pencil then a part of aline is formed. The part of the line will be straight if the surface is planeand curved if the surface is curved.

Thus, if we join any two points with a ruler and extend iton both sides, a line is formed.

A line is indicated by drawing arrow-heads on both sides ofthe part of a line.

The arrow-heads at the ends indicate that the line goes onin both directions. A line has no end, so it has not a definite length.

The name of a line is indicated by two capital letters ofthe English alphabet.

The symbol is placed over the letters as AB, CD.

Also Check: My.hrw.com Algebra 2

How Do You Know If The Discriminant Is Negative

Here are some ways to know that the discriminant is negative, based on the signs of a, b, and c:

• If a and c have the same sign, then ac is positive, which means 4ac is positive, and -4ac is negative. If b is zero, then b2 is zero, and in that case, the discriminant b2 4ac will be negative.
• If a and c have the same sign, but b is not zero, then we must have b2< 4ac in order to have a negative discriminant.

If c is zero, then the discriminant cannot be negative, since b2 4ac reduces to b2, which is always positive or zero .

This makes sense, since a value of c = 0 would give us:

• ax2 + bx + c = 0
• ax2 + bx + 0 = 0
• x = 0

This implies x = 0 or ax + b = 0 as solutions, which leaves us with two real solutions: x = 0 and x = -b/a.

Example 1: Negative Discriminant

Consider the quadratic equation 3×2 + 7 = 0.

Since it has the form ax2 + bx + c = 0, we have a = 3, b = 0, and c = 7.

Note that a and c have the same sign, since a is positive and c is positive .

We also have b = 0.

This means that -4ac will be negative = -84).

Also, b2 = 0.

So, b2 4ac will be negative .

So, the discriminant D = -84 is negative.

Example 2: Negative Discriminant

Consider the quadratic equation 5×2 + 10x + 8 = 0.

Since it has the form ax2 + bx + c = 0, we have a = 5, b = 10, and c = 8.

Note that a and c have the same sign, since a is positive and c is positive .

We also have b not equal to zero .

This means that -4ac will be negative = -160).

So, b2 4ac will be negative .

What Is A Discriminant In Algebra 2

4.3/5Discriminant

The discriminant is the part of the quadratic formula underneath the square root symbol: b²-4ac. The discriminant tells us whether there are two solutions, one solution, or no solutions.

Secondly, how does the discriminant work? The discriminant is the expression b2 4ac, which is defined for any quadratic equation ax2 + bx + c = 0. If you get 0, the quadratic will have exactly one solution, a double root. If you get a negative number, the quadratic will have no real solutions, just two imaginary ones.

In this way, how do you find the discriminant of two variables?

In two variables, the general quadratic equation is ax2 + bxy + cy2 + dx + ey + f = 0, in which a, b, c, d, e, and f are arbitrary constants and a, c 0. The discriminant and the invariant together provide information as to the shape of the curve.

What does the discriminant tell you?

The discriminant tells us the following information about a quadratic equation: If the solution is a real number or an imaginary number. If the solution is rational or if it is irrational. If the solution is one unique number or two different numbers.

Also Check: Unit 1 Geometry Basics Worksheet Answers

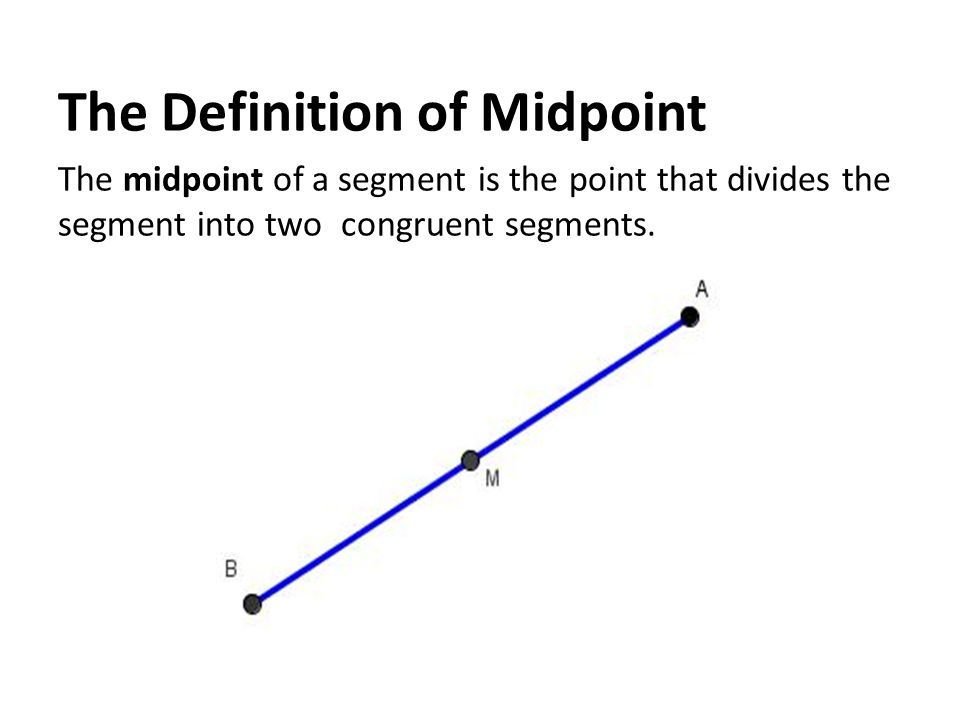
Line Segments And Rays

A line segment, or segment, is a part of a line and contains two endpoints and all points between them. Whereas a ray consists of one endpoint, or initial point, and extends in only one direction. When writing lines, planes, or segments, the order of each point is not important but when naming rays we must always list the endpoint first.

Line Segments in Geometry

Rays in Geometry

Together we will look at the theory behind these terms and accurately identify and represent them all while working through countless examples.

Use In Algebraic Geometry

The typical use of discriminants in algebraic geometry is for studying plane algebraic curves, and more generally algebraic hypersurfaces. Let V be such a curve or hypersurface V is defined as the zero set of a multivariate polynomial. This polynomial may be considered as a univariate polynomial in one of the indeterminates, with polynomials in the other indeterminates as coefficients. The discriminant with respect to the selected indeterminate defines a hypersurface W in the space of the other indeterminates. The points of W are exactly the projection of the points of V , which either are singular or have a tangent hyperplane that is parallel to the axis of the selected indeterminate.

For example, let f be a bivariate polynomial in X and Y with real coefficients, so that f= 0 is the implicit equation of a real plane algebraic curve. Viewing f as a univariate polynomial in Y with coefficients depending on X, then the discriminant is a polynomial in X whose roots are the X-coordinates of the singular points, of the points with a tangent parallel to the Y-axis and of some of the asymptotes parallel to the Y-axis. In other words, the computation of the roots of the Y-discriminant and the X-discriminant allows one to compute all of the remarkable points of the curve, except the inflection points.

Don’t Miss: Laws Of Exponents Worksheets 8th Grade

The Philosophy Of Geometry

What is a geometric point? Is the word ‘point’ the name of an object? of describing the use of a word in the language stands in contrast to the theories of Euclid and Pythagoras about what geometry’s points, lines and planes are .

In Wittgenstein’s logic of language the word ‘point’ in geometry may be defined thus: ‘a geometric point’ is ‘a unique address in the plane’ or, in other words, by the word ‘point’ in plane geometry we mean ‘any unique address in the plane’. This sets aside all metaphysical theories , notions which have their that: “All nouns are names, and the meaning of a name is the object the name stands for.”

An alternative way to “heal the wounded understanding” in philosophy would be simply to at all, but to exclude that word from the language of geometry altogether. We might use e.g. the expression ‘address in the plane’ abbreviated simply to ‘address’.

Now, why do I, who am not a mathematician, presume to discuss this topic ? First, because this is not a topic in mathematics, but rather a . And second, because I only talk about how the word ‘point’ is used in the two geometries I am basically familiar with from school: Euclidean and Cartesian.

Geometry: ‘not defined’ versus ‘undefined’

Outline of this page …

Definition for Orientation

And, further, without such definitions we could not apply pure geometry to the world of our experience , which is of course something we may want to do.

Philosophy Of Mathematics Is The View From Outside Mathematics: What We Imagine About Points Is Of No Importance To Geometry

When I began to teach myself geometry — as any child might do — I used the form of expression ‘Place a point P on line n such that …’ rather than ‘Choose a point P on line n such that …’ — What is remarkable is that this did not matter in the least: it did not affect my proofs.

‘Place a point’ and ‘Choose a point’ can be used interchangeably with no harm done. Use any form of expression you like as long as you don’t break the rules of the game or ask for nonsense .

This is an important method of proof: ‘If p, then q but not-q. Therefore not-p.’ We use this e.g. to prove that two lines have no more than one point in common — by assuming that they have two points in common. But we do not break the rules of the game to do this that is the difference between a postulate and a theorem: we can propose any theorem we like without changing the rules of the game. A theorem is proved or disproved, but we do not prove the contrary of a postulate we simply discard it .

Go ahead! talk about points as though ‘point’ were the name of an invisible object. It does no harm.

Philosophy of Mathematics is the view from outside it is the understanding of the calculus that is not needed for calculating. “What is mathematics?” is not a mathematical question. And mathematicians can dismiss it as a “matter of opinion”, something to chat about.

No theorem necessarily has an application outside geometry

Don’t Miss: My Hrw Algebra 1

Points: A Special Case: No Dimensions

A point is a single location in space. It is often represented by a dot on the page, but actually has no real size or shape.

You cannot describe a point in terms of length, width or height, so it is therefore non-dimensional. However, a point may be described by co-ordinates. Co-ordinates do not define anything about the point other than its position in space, in relation to a reference point of known co-ordinates. You will come across point co-ordinates in many applications, such as when you are drawing graphs, or reading maps.

Almost everything in geometry starts with a point, whether its a line, or a complicated three-dimensional shape.