Geometric Terms And Definitions
We use a point to mark a location or position.
Examples of points are :
the corner of your desk
the tip of your compass needle.
The letters A, B and C identify the points.
Vertices :
The figure alongside contains four points which have been labelled A, B, C and D. These corner points are also known as vertices.
Straight Line :
A straight line, usually just called a line, is a continuous infinite collection of points with no beginning or end which lie in a particular direction.
Line segment :
is the line segment which joins points A and B. We call it line segment AB or line segment BA. It is only part of the line .
Ray :
[AB) is the ray which starts at A, passes through B, then continues on forever in that direction.
Collinear Points :
If three or more points lie on a single straight line, we say that the points are collinear.
Concurrent lines :
If three or more lines meet or intersect at the same point, we say that the lines are concurrent. The lines shown are concurrent at point B.
Parallel lines :
Parallel lines are lines which are always a fixed distance apart and never meet.
Angle :
An angle is made up of two arms which meet at a point called the vertex.
Revolution :
Less than a 1/4 turn.
An acute angle has size between 0° and 90°.
Obtuse angle :
Between 1/4 turn and 1/2 turn.
An obtuse angle has size between 90° and 180°.
Reflex angle :
Between 1/2 turn and 1 turn.
A reflex angle has size between 180° and 360°.
Vertically Opposite Angles :
Transversal :
|
ALGEBRA |
The Etymology Of Geometry Terms
- M.A., Linguistics, University of Minnesota
- B.A., Latin, University of Minnesota
There’s an anecdote about how the philosopher-mathematician Pythagoras overcame a student’s natural dislike of geometry. The student was poor, so Pythagoras offered to pay him an obol for each theorem he learned. Eager for the money, the student agreed and applied himself. Soon, however, he became so intrigued, he begged Pythagoras to go faster, and even offered to pay his teacher. In the end, Pythagoras recouped his losses.
Etymology provides a safety net of demystification. When all the words you hear are new and confusing, or when those around you put old words to strange purposes, a grounding in etymology may help. Take the word line. You put your ruler to paper and draw a line against the straight edge. If you’re an actor, you learn your lines — line after line of text in a script. Clear. Obvious. Simple. But then you hit Geometry. Suddenly your common sense is challenged by technical definitions*, and “line,” which comes from the Latin word linea , loses all practical meaning, becoming, instead, an intangible, dimension-less concept that goes off at both ends to eternity. You hear about parallel lines that by definition never meet each other — except they do in some warped reality dreamt up by Albert Einstein. The concept you have always known as the line has been renamed “line segment.”
Th Grade Geometry Terms
Match the geometric terms to their correct definitions.
| A | |
|---|---|
| two rays with a common endpoint | |
| acute angle | angle measuring less than 90 degrees |
| obtuse angle | angle measuring more than 90 degrees |
| right angle | |
| angle that measures 180 degrees | |
| adjacent angles | |
| complementary angles | the sum of the measures of two angles is 90 degrees |
| supplementary angles | the sum of the measures of two angles is 180 degrees |
| scalene triangle | |
| at least two congruent sides | |
| equilateral triangle | |
| lie in the same plane but do not intersect | |
| trapezoid | exactly one pair of parallel sides |
| parallelogram | both pairs of opposite sides parallel |
| rectangle | a parallelogram with 4 right angles |
| rhombus | parallelogram with 4 congruent sides |
| square | parallelogram with 4 right angles & 4 congruent sides |
| regular polygon | all sides congruent and all sides congruent |
| circle | set of points in a plane that are all the same distance from the center |
| radius | segment that has one endpoint at the center and the other endpoint on the circle |
| diameter | segment that passes through the center of a circle with both endpoints on the circle |
| central angle | an angle with its vertex at the center of a circle |
| chord | segment that has both endpoints on the circle |
| arc |
You May Like: How To Beat Theory Of Everything 2
Geometry Terms And Definitions With Pictures
Definition : Certain statements are being made in order to create new concepts from the existing without leading to wrong results. Such of the statements are called definitions.Examples :1) A triangle is called equilateral if all the sides are of the same length.2) Two angles are called supplementary if their sum is 180°.
Axiom :There are certain statements which are assumed to be true. These statements are called axioms.Examples :1) There is exactly one and only one straight line passing through two given points.2) If n is a natural number, then n+1 is also is also a natural number.Symbol : A symbol is nothing but a particular mark which refers to some information.Some of the symbols and the information indicated by them are given below.
Axiom :There are certain statements which are assumed to be true. These statements are called axioms.Examples :1) There is exactly one and only one straight line passing through two given points.2) If n is a natural number, then n+1 is also is also a natural number.
Congruence :
Congruent means equal in all respects or figures whose shapes and sizes are both the same. Now let us discuss about congruent of triangle.
If the sides and angles of one triangle are equal to the corresponding sides and angles of each other triangle.
In the above pictures the first and third triangles are congruent to each other. So we can say triangle 1 and triangle 3 are congruent.
Conjecture :
A statement until it is proved or disproved called a conjecture.
Geometry Terms And Definitions
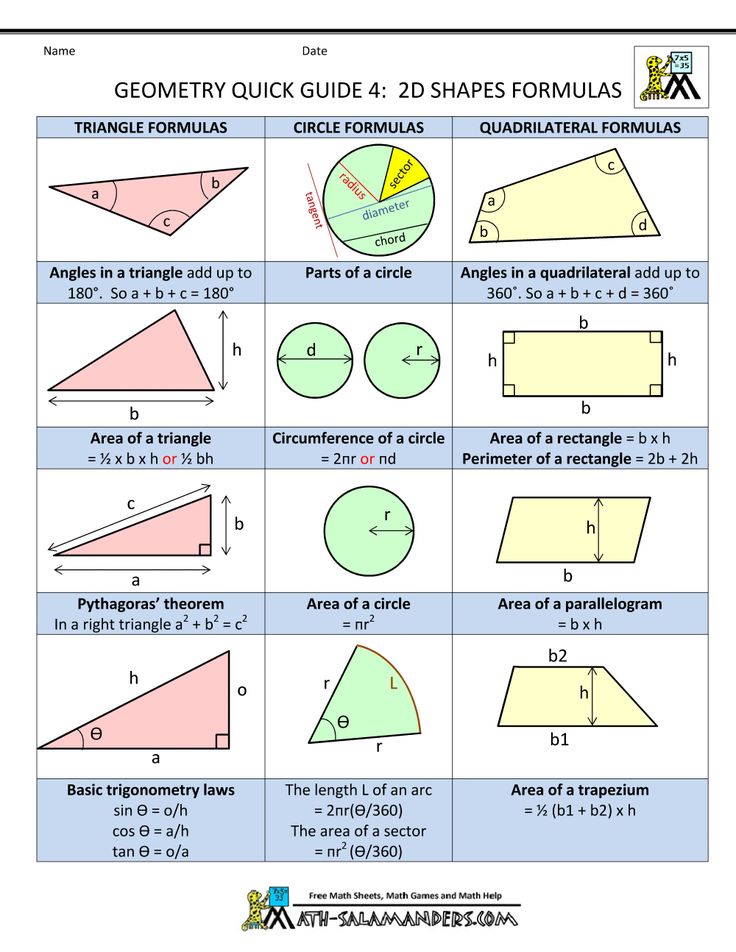
To save you having to refer to a dictionary, weve listed below some of the more common geometry terms and geometry definitions to help you help with your childs geometry homework.
| Term | |
| A location in space a dot on a piece of paper | |
| Line | Connects two points via the shortest path andcontinues indefinitely in both directions |
| Line Segment | Part of a line between two points |
| Perpendicular Line Segment | Line Segments that intersect at an angle of 90° |
| Parallel Line Segments | Line segments that never intersect |
| Right Angle | An angle that measures 90° |
| Acute Angle | An angle that measures less than 90° |
| Obtuse Angle | An angle that measures more than 90° |
| Vertex | Point at which two line segments intersect |
| A triangle with all three sides with different lengths | |
| Isosceles Triangle | A triangle with two equal length sides |
| Equilateral Triangle | A triangle with all three sides of equal length |
| Distance from center of a circleto any point on that circles circumference. | |
| Diameter | A line segment joining two points ona circles circumference and passes through thecircles center |
| Circumference | Distance around a circle |
| Chord | A line segment joining two points on a curve. |
| Arc |
Also Check: Who Are Paris Jackson’s Biological Parents
Open And Closed Figures
A point is a small dot which is the starting point of a line segment. By definition, a line segment is a part of a line in which a narrow lane is connecting two points within a line. Different numbers of line segments give us different figures and such figures may be either open figure or closed shapes or figures.
Print Resource Or Save As Pdf
Print feature not currently compatible with Firefox.
A useful reference of geometric terms and their definitions.
Attributes and Spatial Properties Qualities of a figure, including sides, size, angles, etc.
Two-Dimensional Figures
- Circle: A two-dimensional shape in which all points on the curved line are equidistant from a center point.
- Triangle: A closed figure with three sides.
- Rectangle: A two-dimensional, closed, four-sided figure with four right angles.
- Rhombus: A closed four-sided figure with parallel opposite sides. A square is a special kind of rhombus. Sometimes called a diamond.
- Square: A special type of rectangle that has equilateral sides and parallel opposite sides.
- Pentagon: A closed figure with five sides.
- Hexagon: A closed figure with six sides.
- A closed figure with seven sides.
- A closed figure with eight sides.
Three-Dimensional Figures
Read Also: Lesson 9.5 Practice B Geometry Answers
These Are The Geometry Terms You Might Not Have Heard Before
No part of math is more confusing than geometry. The main reason being the numerous terms which students get entangled in. In this ScienceStruck post, we give you a list of the basic terms used in geometry, to make understanding this branch of mathematics easier.
Like it? Share it!
No part of math is more confusing than geometry. The main reason being the numerous terms which students get entangled in. In this ScienceStruck post, we give you a list of the basic terms used in geometry, to make understanding this branch of mathematics easier.
How To Measure Angles And Types Of Angles
An angle consists of two rays with a common endpoint. The two raysare called the sides of the angle and the common endpoint is the vertex of the angle.
Each angle has a measure generated by the rotation about the vertex. The measure is determined bythe rotation of the terminal side about the initial side. A counterclockwise rotation generates apositive angle measure. A clockwise rotation generates a negative angle measure. The units used tomeasure an angle are either in degrees or radians.
Angles can be classified base upon the measure: acute angle, right angle, obtuse angle, and straightangle.
If the sum of measures of two positive angles is 90°, the angles are called complementary.
If the sum of measures of two positive angles is 180°, the angles are called supplementary.
Examples:
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers
Fundamental Concepts Of Geometry
This video explains and demonstrates the fundamental concepts of geometry: points,lines, ray, collinear, planes, and coplanar. The basic ideas in geometry and how we represent themwith symbols.
A point is an exact location in space. They are shown as dots on aplane in 2 dimensions or a dot in space in 3 dimensions. It is labeled with capital letters. It doesnot take up any space.
A line is a geometric figure that consists of an infinite number ofpoints lined up straight that extend in both directions for ever .A line is identified by a lower case letter or by two points that the line passes through. There isexactly 1 line through two points. All points on the same line are called collinear. Points not onthe same line are noncollinear.
Two lines are either parallel or they will meet at a point of intersection.
A line segment is a part of a line with two endpoints. A line segmentstarts and stops at two endpoints.
A ray is part of a line with one endpoint and extends in one directionforever.
A plane is a flat 2-dimensional surface. A plane can be identifiedby 3 points in the plane or by a capital letter. There is exactly 1 plane through three points. Theintersection of two planes is a line.
Coplanar points are points in one plane.
Look Up The Meaning Of Math Words
- Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
- B.A., Physics and Mathematics, Hastings College
This is a glossary of common mathematical terms used in arithmetic, geometry, algebra, and statistics.
Abacus: An early counting tool used for basic arithmetic.
Absolute Value: Always a positive number, absolute value refers to the distance of a number from 0.
Acute Angle: An angle whose measure is between 0° and 90° or with less than 90° radians.
Addend: A number involved in an addition problem numbers being added are called addends.
Algebra: The branch of mathematics that substitutes letters for numbers to solve for unknown values.
Algorithm: A procedure or set of steps used to solve a mathematical computation.
Angle: Two rays sharing the same endpoint .
Angle Bisector: The line dividing an angle into two equal angles.
Area: The two-dimensional space taken up by an object or shape, given in square units.
Array: A set of numbers or objects that follow a specific pattern.
Attribute: A characteristic or feature of an objectsuch as size, shape, color, etc.that allows it to be grouped.
Average: The average is the same as the mean. Add up a series of numbers and divide the sum by the total number of values to find the average.
Base: The bottom of a shape or three-dimensional object, what an object rests on.
Base 10: Number system that assigns place value to numbers.
Bar Graph: A graph that represents data visually using bars of different heights or lengths.
You May Like: What Is Biomass In Biology
Did You Know
The word Geometry comes from the ancient Greek words geo and metron, that mean earth and measurement respectively.
Geometry can be called a study of the shape, size, and position of objects. It is considered to be difficult due to the many terms used in the subject, and also due to the fact that one has to understand the subject it cannot be learned by rote. Most of these terms can be confusing to students, and in addition to these terms, there are various theorems, laws, and definitions that have to be understood as well.
In this article, we have given you a list of the definitions of some of the basic terms used in geometry. It should be noted that neither is this list for beginners, not is it for advanced students. It is meant to be a ready reference for those who have studied geometry earlier.