Can Power Ever Be Negative
Consider this question which HAS definitely been asked but i ask you now to question your first inclination to just ‘do the question’ and explain the thought process. Restrictions: assume you only know work energy theorem, and the definition of power So no potential energy as it shouldn’t require it. and of course you have your kinemtaic equations with newtons laws.
“A 20.0-kg rock is sliding on a rough, horizontal surface at 8ms^-1and eventually stops due to friction. The coefficient ofkinetic friction between the rock and the surface is 0.200. Whataverage power is produced by friction as the rock stops?”
so, going the long route
work total = work done by friction
= ^2 - ^2 = -640J
time taken for work:v = v_0 + at
t = /a
=4.08s
Therefore, average power should be
average power = DELTA work/ DELTA time
= / =-157watts
i double checked everything and looked at other websites and it gives no mention of negative power… so what do you guys think?
- 1$\begingroup$There’s a duality – positive work is always associated with negative work elsewhere in the system.$\endgroup$;SteveJan 14 ’18 at 13:09
- $\begingroup$If I give you x blobs per second then I lose x blobs per second. For “blobs” read “energy”.$\endgroup$
Assume that the system under consideration is the rock.
So your statement
Keep in mind that the work done by friction is negative
If perhaps better written as
Keep in mind that the work done on the rock by the external force is negative
Can You Have Negative Work In Physics
4.7/5physicsworkWork cannegativeifhas aworkIfhas adoes negative workanswer here
Negative work occurs when the force acting on an object is opposite in direction to the displacement. So when you lower the book, you are applying an upwards force to it, but its displacement is downwards.
One may also ask, why is work done negative? NEGATIVE WORK:The work done is said to be negative work when force and displacement are in opposite direction. example: When an object is thrown upwards,the force CTS in downward direction whereas displacement acts in upward direction.
Also know, what is negative work done with example?
Negative work. If the force and the displacement are in opposite directions, then the work is said to be negative. For example if a ball is thrown in upwards direction, its displacement would be in upwards direction but the force due to earth’s gravity is in the downward direction.
How do you calculate negative work?
Remember that Force is Mass times Acceleration. If Acceleration is negative , then Force is negative. Since Work is Force times Distance, if Force and Distance are different signs, then Work is negative.
Can The Work By Static Friction On An Object Be Negative
Asked by user14250
We know that static friction acts between two surfaces in contact when they are not moving relative to each other . This question was inspired by my previous question Can the work by kinetic friction on an object be zero? where I considered the cases of positive, negative and zero work done by kinetic friction. I did a similar analysis for static friction, and the following points discuss the case of zero and positive work:
-
Zero work Suppose a block is kept on a rough surface. When a small force is supplied the object does not move relative to the surface due to the static friction force supplied by the surface on the block which is equal and opposite to the applied force. Here, since the displacement is zero, the work done by either of the two forces is zero.
-
Positive work The work done by static friction on an object moving along with an accelerating belt is positive with respect to the ground frame as the displacement and the friction force act along the same direction .
But, Im unable to think of cases when the work done by static friction is negative. Is it possible for static friction to do negative work? If not, kindly specify the reason behind it.
Please note: Ive read the answers for the following questions but none of them discuss the case of negative work done by static friction.
Also Check: Kuta Angle Addition Postulate
Can Work Done Ever Be Negative
If a car is moving towards me and I push against the bonnet with a force $F$, but it makes little difference so the car pushes me backwards in a straight line for distance $x$, have I done $-Fx$ work on the car or have I done no work on it?
You can think of negative work as if you were pulling energy out of the system. In your example, you are indeed trying to brake the car and you do that by removing $W=-Fx$ Joules from it’s kinetic energy.
The force that the car applies on you has a displacement which is in the same direction as the force so that force due to the car does positive work on you.
The force that you applied on the car has a displacement which is in the opposite direction to the force so that force due to you does negative work on the car.
Work Has Units Of Energy

The total energy of a system is its internal or thermal energy plus its mechanical energy. Mechanical energy can be divided into energy of motion and “stored” energy . The total mechanical energy in any system is the sum of its potential and kinetic energies, each of which can take various forms.
Kinetic energy is energy of motion through space, both linear and rotational. If a mass m is held a distance h above the ground, its potential energy is mgh. Where the acceleration due to gravity, g, has the value of 9.80 m/s2 near Earth’s surface.
If the object is released from rest at height h and allowed to fall downward to Earth , its kinetic energy at impact is mv2 = mgh, as all of the energy has been converted from potential to kinetic during the fall . At all times, the sum of the potential energy of the particle and its kinetic energy remains constant.
- Because force has units of;newtons; in the SI system and distance is in meters, work and energy in general have units of kgm2/s2. This SI unit of work is known as the;Joule.
Don’t Miss: Is Michael Jackson The Biological Father Of Paris
Work And Kinetic Energy
- Represent the work done by any force
- Evaluate the work done for various forces
In physics, work is done on an object when energy is transferred to the object. In other words, work is done when a force acts on something that undergoes a displacement from one position to another. Forces can vary as a function of position, and displacements can be along various paths between two points. We first define the increment of work dW done by a force \overset acting through an infinitesimal displacement d\overset as the dot product of these two vectors:
Then, we can add up the contributions for infinitesimal displacements, along a path between two positions, to get the total work.
Work Done by a Force
The work done by a force is the integral of the force with respect to displacement along the path of the displacement:
The vectors involved in the definition of the work done by a force acting on a particle are illustrated in .
Figure 7.2 Vectors used to define work. The force acting on a particle and its infinitesimal displacement are shown at one point along the path between A and B. The infinitesimal work is the dot product of these two vectors; the total work is the integral of the dot product along the path.
Can Force Be Negative
To answer the question can force be negative, we need to understand the concept of positive direction and negative direction.
- Force is negative If the applied force is in opposite direction to the displacement of the moving object.
- Forces that are aimed at the;right;are usually called;positive;forces.;
- Forces that are aimed to the;left;are usually said to be in a;negative;direction.
Recommended Reading: Afda Mean Median Mode Range Practice Answer Key
Coasting Down A Mountain Road
Consider the case of a vehicle that starts at rest and coasts down a mountain road, the workenergy principle helps compute the minimum distance that the vehicle travels to reach a velocity V, of say 60;mph . Rolling resistance and air drag will slow the vehicle down so the actual distance will be greater than if these forces are neglected.
Let the trajectory of the vehicle following the road be X which is a curve in three-dimensional space. The force acting on the vehicle that pushes it down the road is the constant force of gravity F = , while the force of the road on the vehicle is the constraint force R. Newton’s second law yields,
- F
- ft . }=8.3}},\quad }\quad s=8.3}}\approx 2000}.}
This formula uses the fact that the weight of the vehicle is W = mg.
How Can Work Be Negative
- 0
negative
- 1,892
- 461
Ellipses said:Hello everyone.I understand the concept of work in general, but the concept of negative work still somewhat baffles me. One of my main problems is this: according to my textbook, 3 conditions must be met in order for work to be done, and one of them is “at least part of the force must be in the same direction as the displacement.”Well, how can negative work occur if the force in displacement are going in opposite directions?Thanks for the help!
Don’t Miss: What Is Hydraulic Lift In Physics
Conceptually What Is Negative Work
I’m having some trouble understanding the concept of negative work. For example, my book says that if I lower a box to the ground, the box does positive work on my hands and my hands do negative work on the box. So, if work occurs when a force causes displacement, how does negative work happen? Are my hands displacing anything?
- $\begingroup$Displacement is not always caused by the force that you want to find it’s work. In your example of lowering a box, gravity must be considered.$\endgroup$;MostafaMay 24 ’13 at 22:21
- $\begingroup$Your book may be wrong. It’s not going down that makes a negative work, but, as explained by joshphysics, it’s the slowing down of the movement.$\endgroup$;fffredMay 25 ’13 at 7:49
- $\begingroup$@ffred The book is right, since holding an object in a gravitational field results in a normal force from the hand, and since the motion is downward it is in fact negative work$\endgroup$;yoel halbApr 17 ’14 at 16:19
- $\begingroup$Slightly tangential but it may help get a feeling for what is meant by negative work, have a look at the different conventions for writing out the first law of thermodynamics. You can see that what is defined as positive work under one convention is negative work in another.$\endgroup$
Work Done By Constant Forces And Contact Forces
The simplest work to evaluate is that done by a force that is constant in magnitude and direction. In this case, we can factor out the force; the remaining integral is just the total displacement, which only depends on the end points A and B, but not on the path between them:
We can also see this by writing out in Cartesian coordinates and using the fact that the components of the force are constant:
shows a person exerting a constant force \overset along the handle of a lawn mower, which makes an angle \theta with the horizontal. The horizontal displacement of the lawn mower, over which the force acts, is \overset. The work done on the lawn mower is W=\overset·\overset=Fd\,\text\,\theta , which the figure also illustrates as the horizontal component of the force times the magnitude of the displacement.
Figure 7.3 Work done by a constant force. A person pushes a lawn mower with a constant force. The component of the force parallel to the displacement is the work done, as shown in the equation in the figure. A person holds a briefcase. No work is done because the displacement is zero. The person in walks horizontally while holding the briefcase. No work is done because \text\,\theta is zero.
In , where the person in is walking horizontally with constant speed, the work done by the person on the briefcase is still zero, but now because the angle between the force exerted and the displacement is 90\text and \text\,90\text=0 .
Don’t Miss: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate Answers
Can Work Done By A Body Be Negative Or Positive
Work is the product of the component of the force in the direction of the displacement and the magnitude of this displacement.
Mathematically,
W = d = F. d
- W is the work done by the force.
- F is the force, d is the displacement caused by the force
- is the angle between the force vector and the displacement vector
A Couple Of Shockers:
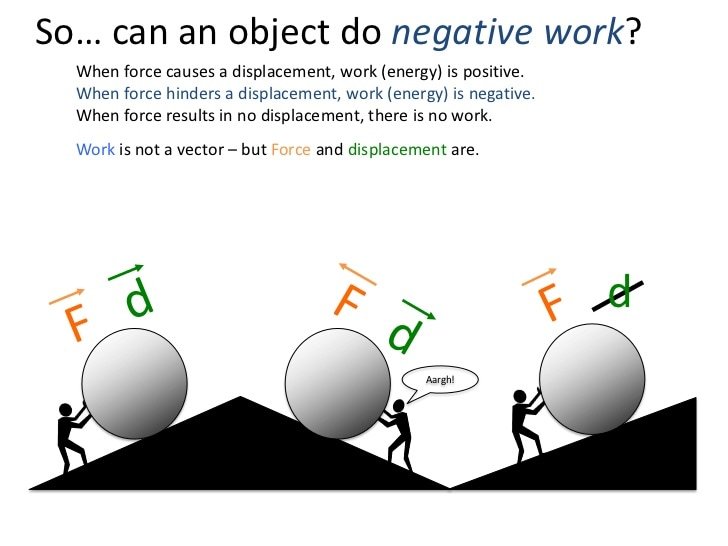
Undoubtedly, you have been taught that “Work equals force timesdistance.” Brace yourself. Work is sometimes force timesdistance, but not always. Work is more subtle thanthat, and in order to understand energy, you have to understand workto a greater depth.
If you think that “work equals force times distance,” then youprobably think that you automatically do work every time you exert aforce. That’s not true, either!
Why? Well, the work/energyequation says that work done equals the object’s change in kinetic energy. More simply:
Work = Change in Kinetic Energy
This means that if an object’s kinetic energy doesn’t change, thenno work has been done on the object – whether or not a force has beenexerted.
In the diagram above, the green block is moving to the right. Thered force F1 does work on the block because it has a component in the direction of motion. The blue force F2 does NOT do work on the block, because it does not have a component in the direction of motion.
So, an object’s kinetic energy will only change if the forceacting on the object changes the object’s speed. This will onlyhappen if there is a component of the force in the direction that theobject moves.
Therefore, a force will do work onlyif the force has a componentin the direction that the object moves.
Don’t Miss: Unit 1 Test Geometry Basics Answers Key
How To Calculate Work
You can calculate total work by adding up the amount of work done by different forces in a problem. In all cases, calculating work requires a complete understanding of the vectors in the problem, not merely the numbers that go with them. You will need to put basic trigonometry to use.
- Note: In real life, when a force acts on an object besides gravity, it is unlikely to be constant. Any force F you see mentioned in these examples can be assumed to be a constant force. When forces vary, the relationships noted here remain valid, but you will need to perform integral calculus to solve the associated problems.
Example: A dog pulling a 20-kg child-sled combination across a horizontal snowfield accelerates from rest to a velocity of 5 m/s over the course of 5 seconds . How much work does the dog do on the child-sled combination? Assume friction is negligible.First, you calculate total force applied by the dog to the child and sled: F = ma = = 20 N. Displacement is average velocity /2 multiplied by time t , which is 12.5 m. Thus total work is = 250 J.
- How would you solve this problem using the work-energy theorem instead?
Can Work Be Negative
Work is done when a force acting on a body displaces it in the direction of a force. For instance, the work done by a moving object equals 1 Joule when a force of 1 Newton is applied over 1 meter of distance. Since the applied force can be negative or positive, therefore, work can be negative or positive.The motion of a body against force of friction is an example of negative work.
Read Also: Algebra Road Trip Project Answer Key
Are There Any Known Negative Heat Capacities
If we take heat capacity to be defined as “the ratio of the heat added to the temperature rise”:
$$ C=\frac Q_}\theta}$$
then this leads me to ask: can this ever be negative? That is to say, are there any materials which cool as you add heat to them?
- $\begingroup$Are you set on materials, or would any system do?$\endgroup$;user10851Feb 1 ’16 at 1:17
- 2;Maxim UmanskyFeb 1 ’16 at 1:18
- 2Feb 1 ’16 at 1:44
- 1$\begingroup$a black hole temperature decreases as its mass increases : $T = }$$\endgroup$;user46925
There are certainly systems that have negative heat capacities, and in fact they come up all the time in astrophysics.
As a general rule, gravitationally bound systems have negative heat capacities. This is because in equilibrium , some form of the virial theorem will apply. If the system has only kinetic energy $K$ and potential energy $U$, then the total energy is of course $E = K + U$, where $E < 0$ for bound systems. In virial equilibrium where the potential energy is purely gravitational, then we also have $K = -U/2$. As a result, $K = -E$, and so adding more energy results in a decrease in temperature.
At some level, this all comes down to what you’re defining as temperature. Recall that temperature simply accounts for the flow of heat into whatever you’ve defined as your thermometer. If your thermometer couples to translational kinetic energy but not to gravitational potential energy, then you get the situation above.
$$C_V \stackrel \frac = -\frac Nk_B$$
EDIT: