What Is Angle In Math

Values Of The Tangent Function

What is an Angle? | Different Types of Angles | Geometry | Math | LetsTute

There are many methods that can be used to determine the value for tangent such as referencing a table of tangents, using a calculator, and approximating using the Taylor Series of tangent. In most practical cases, it is not necessary to compute a tangent value by hand, and a table, calculator, or some other reference will be provided.

Vertical And Adjacent Angles

When two straight lines intersect at a point, four angles are formed, for example, “A,””B,””C,” and “D” angles.

A pair of angles opposite each other, formed by two intersecting straight lines that form an “X”-like shape, are called vertical angles or opposite angles. The opposite angles are mirror images of one another. The degree of angles will be the same. Those pairs are named first. Since those angles have the same measure of degrees, those angles are considered equal or congruent.

For example, pretend that the letter “X” is an example of those four angles. The top part of the “X” forms a “V” shape, that would be named “angle A.” The degree of that angle is exactly the same as the bottom part of the X, which forms a “^” shape, and that would be called “angle B.” Likewise, the two sides of the “X” form “> ” and “< ” shapes. Those would be angles “C” and “D.” Both C and D would share the same degrees, as they are opposite angles and are congruent.

In this same example, “angle A” and “angle C” and are adjacent to each other, they share an arm or side. Also, in this example, the angles are supplementary, which mean that each of the two angles combined equals 180 degrees . The same can be said of “angle A” and “angle D.”

Alternative Ways Of Measuring The Size Of An Angle

There are several alternatives to measuring the size of an angle by the angle of rotation.The slope or gradient is equal to the tangent of the angle, or sometimes the sine a gradient is often expressed as a percentage. For very small values , the grade of a slope is approximately the measure of the angle in radians.

Inrational geometry the spread between two lines is defined as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines.

Astronomers measure angular separation of objects in degrees from their point of observation.

0.5° is approximately the width of the sun or moon.
1° is approximately the width of a little finger at arm’s length.
10° is approximately the width of a closed fist at arm’s length.
20° is approximately the width of a handspan at arm’s length.

These measurements clearly depend on the individual subject, and the above should be treated as rough rule of thumb approximations only.

In astronomy, right ascension and are usually measured in angular units, expressed in terms of time, based on a 24-hour day.

Unit
160 minute

Don’t Miss: Geometry Dash Eric Van Wilderman

Acute And Obtuse Angles

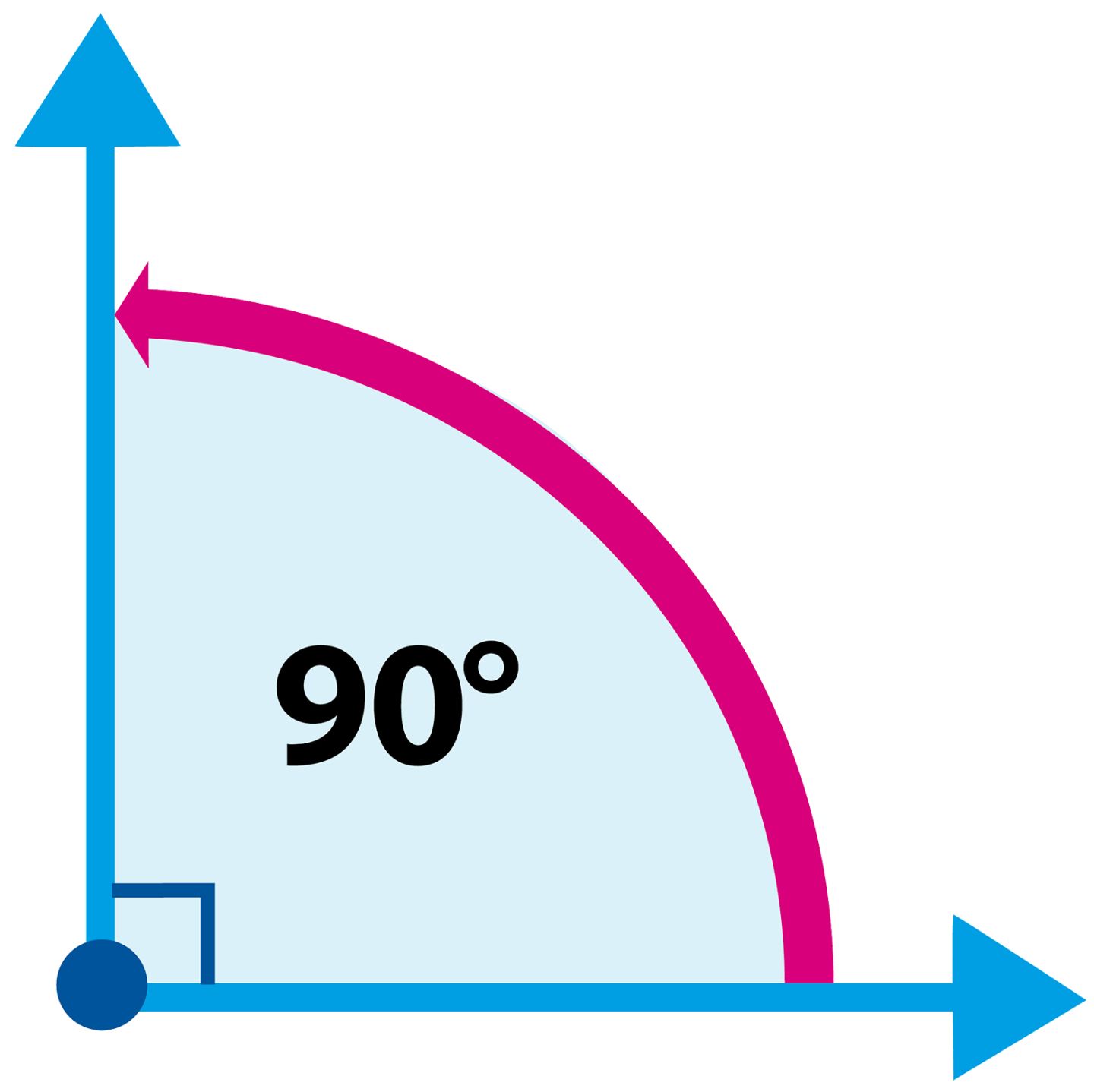
Another way to classify angles by their measures is to consider whether the angle’s measure is greater or less than 90 degrees. If an angle measures less than 90 degrees, it is called an acute angle. If it measures more than 90 degrees, it is called an obtuse angle. Right angles are neither acute nor obtuse. They’re just right.

How To Draw Angles

Welcome to Grade 4!: February/March Math Workshop

Angles less than 180° can be drawn using a protractor by following the steps below:

Draw a straight line of any measurement. The straight line will act as the arm of the angle.
Place the middle of the protractor at the vertex dot and ensure the mark on the line and the protractor flashes center.
Find the given angle on the protractor scale and mark a small dot at the protractors edge.
Now, remove the protractor and then use a ruler to join the dot with the vertex mark.
Label the angle with capital letters

Example 3

Explanation

Draw a straight line of any dimension and place a dot along the line.

Place the base of the protractor on the line such that its center coincides with the mark.

Move anticlockwise along the protractor scale and place a dot at 50°.
Using a ruler, join the dot with the mark on the line.
Label your diagram such that A and C are the sides and B is the vertex of the angle.

You can use the same procedure to draw any angle less than 180°.

You May Like: Ccl4 Molecular Geometry

Can Three Angles Form A Linear Pair

A linear pair is defined as adjacent angles that adds upto 180° or two angles which when combined forms a line or a straight angle. We can have three angles that are supplementary, but not necessarily adjacent. So, they are supplementary but not necessarily a linear pair as they dont always form a straight line.

Converse Of Corresponding Angle Theorem

The converse of a corresponding angle theorem states that,

If the corresponding angles in the two intersection regions are congruent then, the two lines are said to be parallel.

Take Note:

A pair of corresponding angles lie on the same side of the transversal line.
One exterior angle and one interior angle comprise up the corresponding pair of angles.
Not all corresponding angles are equal. If the transversal intersects two parallel lines, the corresponding angles are equal. When the transversal intersects non-parallel lines, the resulting angles are incongruent and unrelated.
Supplementary angles are formed when the transversal perpendicularly intersects two parallel lines.
If the lines are parallel, exterior angles on the same side of the transversal are supplementary. Similarly, if the two lines are parallel, the interior angles are supplementary.

Also Check: The Angle Addition Postulate Answers

Glossary And Terms: Angles

Acute angle – Any angle smaller than 90°.Adjacent angles – Adjacent angles are two angles that share a common vertex and one common side. They do not overlap.In the picture to the right, angles cad and cab are adjacent angles.

AdjoiningAlternate exterior anglesAlternate interior anglesAngleCentral angleComplementary angles Corresponding anglesExterior angleInscribed angleObtuse angleProtractorRight angleStraight angleSupplementary anglesTransversalMore Math Glossaries and Terms

Maximizing An Angle Based On Certain Constraints

Angles – Types and definition – Mathematics for kids

$A $ and $B\ \ $ are the vertices of $\triangle ABC$ where $C$ is variable. Find the value of $x$ when angle $ACB$ is maximum.

Now geometry’s never really been my strong point, so I decided to go with a bit of calculus.First, I used the sine rule:$$\mathrm} $$where R is the radius of the circumcircle. I note that for angle C to be maximum, sinC should be maximum. As such, R must be minimum.Next, I used the relation $$\mathrm\cdot\sqrt}} $$where $\mathrmABC=\frac}$.

A bit of comparatively lengthy differentiation gives me the value of $x$ as $\sqrt$.

When I go through the solutions, it’s simply been stated:

For angle ACB to be maximum, the circle passing through A,B will touch the X-axis at C.

Beyond this, it’s been solved using the very simple $\mathrm$, where O is the origin. So the above statement seems to be the difference between a lengthy differentiation and a one line solution.

It’s getting a little difficult for me to see why the above statement should be intuitive. Could someone shed a bit more light on it for me, and possibly provide an intuitive proof?

Also Check: Geometry Segment Addition Postulate Worksheet

Positive And Negative Angles

Although the definition of the measurement of an angle does not support the concept of a negative angle, it is frequently useful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions relative to some reference.

In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns. With positive angles representing rotations toward the positive y-axis and negative angles representing rotations toward the negative y-axis. When Cartesian coordinates are represented by standard position, defined by the x-axis rightward and the y-axis upward, positive rotations are anticlockwise and negative rotations are clockwise.

In many contexts, an angle of is effectively equivalent to an angle of “one full turn minus “. For example, an orientation represented as 45° is effectively equivalent to an orientation represented as 360° 45° or 315°. Although the final position is the same, a physical rotation of 45° is not the same as a rotation of 315° .

Tangent Is A Periodic Function

A periodic function is a function, f, in which some positive value, p, exists such that

f = f

for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f. The period of the tangent function is , and it has vertical asymptotes at odd multiples of . We can write this as:

tan = tan

To account for multiple full rotations, this can also be written as

tan = tan

where n is an integer.

Unlike sine and cosine, which are continuous functions, each period of tangent is separated by vertical asymptotes.

Example:

tan = tan = tan = 1

Also Check: Can Work Be Negative Physics

What Is Meant By Adjacent And Vertical Angles

If two angles share a common vertex and the common arm, then the angles are called adjacent angles. Vertical angles are the angles opposite each other when two lines intersect.

Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!

Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz

Different Types Of Angles In Geometry

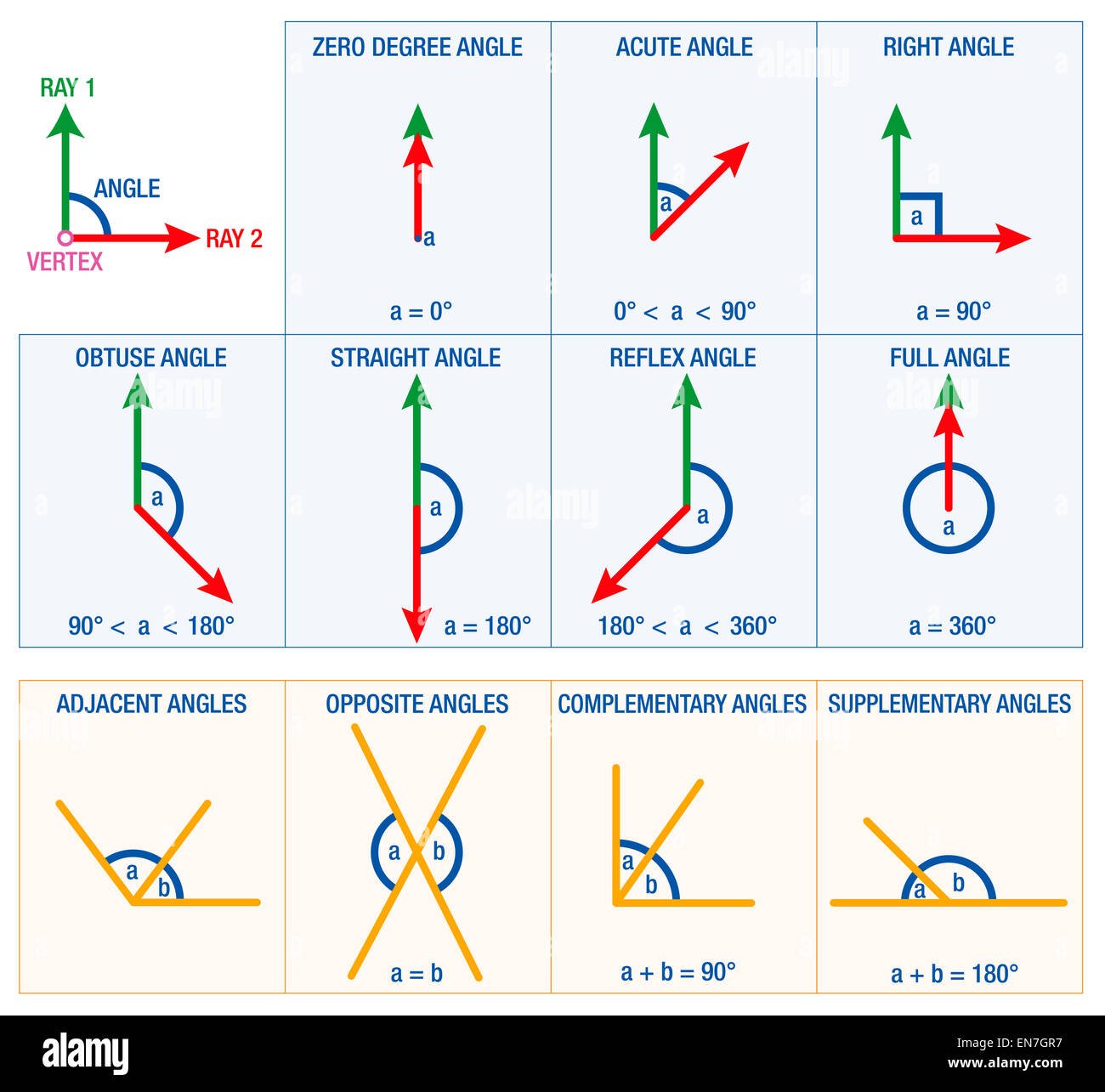
Angles from geometry and mathematics science, like ACUTE ...

In this section we know about definition of angle in geometry and its types of angles like Interior and Exterior of an angle, Zero Angle, Acute Angle, Right Angle, Obtuse angle, Straight Angle, Reflex Angle & Complete angle

What is Angle

An angle is formed when two rays originate from same end point. The two rays formed an angle are calledarms or sides of the angle and the end point is called the vertex of the angle.

An angle is denoted by the symbol

Here the rays OP, OQ from an angle denoted by POQ or QOP.

Sometimes, the above angle by written by the letter at the vertex of the angle. For example , in the above figure the angle POQ is also denoted by O or angle O

In the above figure angles are named as follows

POR , POQ & ROQ

The standard unit for measuring an angle is degree.

Degree is defined as 360th part of one complete revolution.

One complete revolution is equal to 360 degree or 360o

One degree is further divided into 60 equal parts. Each equal part is called one minute and it is written as 1

1o = 60

One minute is further divided into 60 equal parts. Each equal part is called one second and it is written as 1

1 = 60

Corresponding Angles Formed By Parallel Lines

When two parallel lines intersect with a third line , the angles that share the same relative position at each intersection are said to be corresponding angles.

Say, for example,

The figure above describes corresponding angles. Thus, interpreting the figure:

Line 1 and Line 2 are parallel lines
Line 3 intersects with Lines 1 and 3
Angles 1 and 2 have the same relative position.

Thus, we can conclude that angles 1 and 2 are corresponding angles.

How To Construct Angles

We use a protractor to construct angles. Lets draw a 50° angle.

Step 1: First, draw a ray OB and align the protractor with OB as shown.

Step 2: Place a point above the marking on the protractor that corresponds to 50°.

Step 3: Remove the protractor and draw a ray beginning at O that passes through this point. Thus, AOB is the required angle, that is AOB = 50°

Note: If the ray extends in the other direction, we measure the angle from the 0° mark on the bottom-left.

The image given below shows how to draw a 50° angle when the ray is pointing in another direction.

Important Notes on Angles

Proof Of The Corresponding Angle Theorem

What are Adjacent Angles? | Math with Mr. J

Assume line A and line B are parallel.

Prove that the corresponding angles are equal.

Suppose line A is parallel to line B. If a distinct line M intersects with lines A and B, then we can label the angles ,, and , as shown in the figure.

Since and are in a straight line, by linear pair postulate, we can conclude that the sum of and is 180°. Thus, =180°-.

Since and form the interior and exterior angles of the parallel lines, it also follows that is supplementary to . Thus, we can conclude that =180°-. Then, we will have

=180°- and =180°-.

Hence, =.

Therefore, the pair of corresponding angles are equal to each other.

Recommended Reading: What Is The Molecular Geometry Of Ccl4

Three Main Types Of Angles

Acute – any angle which measures less than 90 degrees. These angles appear “sharp,” like the blade on a knife.

Example: The angle ABC measures 40 degrees. Angle ABC is acute.

Right – any angle which measures exactly 90 degrees. These are like the edges of a wooden block.

Sample: The angle CAT measures 90 degrees. The angle CAT is a right angle.

Obtuse – any angle which measures more than 90 degrees but less than 180 degrees. These are “fat” angles that are very wide.

Sample: angle DEF measures 125 degrees. Then angle DEF is obtuse.

What Is An Angle

Lesson materials located below the video overview.

A natural question: What is an angle?

Loosely speaking, an angle is simply an amount of turning.

If I were to twirl in place and end up back facing you, we would say I turned through an angle of one full turn. If I did this a second time wed say I had turned through an angle of two full turns.

Twirling through an angle of half a turn would land me with my back to you, as would a twirl of one-and-half full turns, and an angle of 99.5 full turns.

Heres pencil pointing to the right.

If we turn this pencil a quarter-turn about its end, say in a counter clockwise direction, then its new position relative to its starting position will be as shown.

The following picture shows \ of a turn.

And the following shows a half turn, a full turn, and two full turns of pencils with different starting positions.

Notice that any full count of turns gives the same final effect as applying no turns at all.

Don’t Miss: Unit 1 Test Geometry Basics Answers Key

Interior And Exterior Of An Angle

Interior of an angle : The part of the plane which is within the arms of an angle produced indefinitely is called the interior of the angle.

Exterior of the angle:The part of the plane which is outside the arms of an angle produced indefinitely is called the exterior of the angle.

For example:

In the above figure all points in the plane of POQ can be divided into three regions

On the angle : The points on the angle are P, Q & R

Interior of the angle : The points in the interior C & D

Exterior of the angle : The points in the exterior A, B & E

Types of Angles:

What Will I Learn From This Article

After reading this article, you will be able to:

properly define corresponding angles
know the corresponding angle theorem
determine corresponding angles based on figures
prove the corresponding angle theorem
prove the converse of the corresponding theorem and
apply the theorems in solving problems involving corresponding angles.

Recommended Reading: What Is The Shape Of Ccl4

How To Measure An Angle

We use protractors to measure angles. See the image given below. We can see AOB. Lets try and see if we can find out what type of angle is AOB. Doesn’t it look like an acute angle? This means that its measure is greater than 0° and less than 90°. Let us learn how to measure an angle using a geometrical instrument protractor.

Steps to measure AOB.

Step1: Align the protractor with the ray OB as shown below. Start reading from the 0° of the protractor.

Step 2: The number on the protractor that coincides with the second ray is the measure of the angle. Measure the angle using the number on the “lower arc” of the protractor. Thus, AOB = 37°

Next, let us try to measure this AOC.

Step 1: Measure the angle from the 0°.

Step 2: The number on the “top arc” of the protractor that coincides with OA is the measure of AOC. Thus, AOC = 143°

Proof Of The Converse Of The Corresponding Angle Theorem

Assume the corresponding angles are equal.

Prove that line P and line Q are parallel.

Suppose two distinct lines P and Q are cut by a transversal line T and assuming that the corresponding angles are equal, then we can label angles as and , as shown in the figure.

Therefore, $\overleftrightarrow \overleftrightarrow$.

Recommended Reading: Behaviorism Was Founded By

Don't Miss