How To Understand Logarithms
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 28 people, some anonymous, worked to edit and improve it over time. This article has been viewed 359,762 times.Learn more…
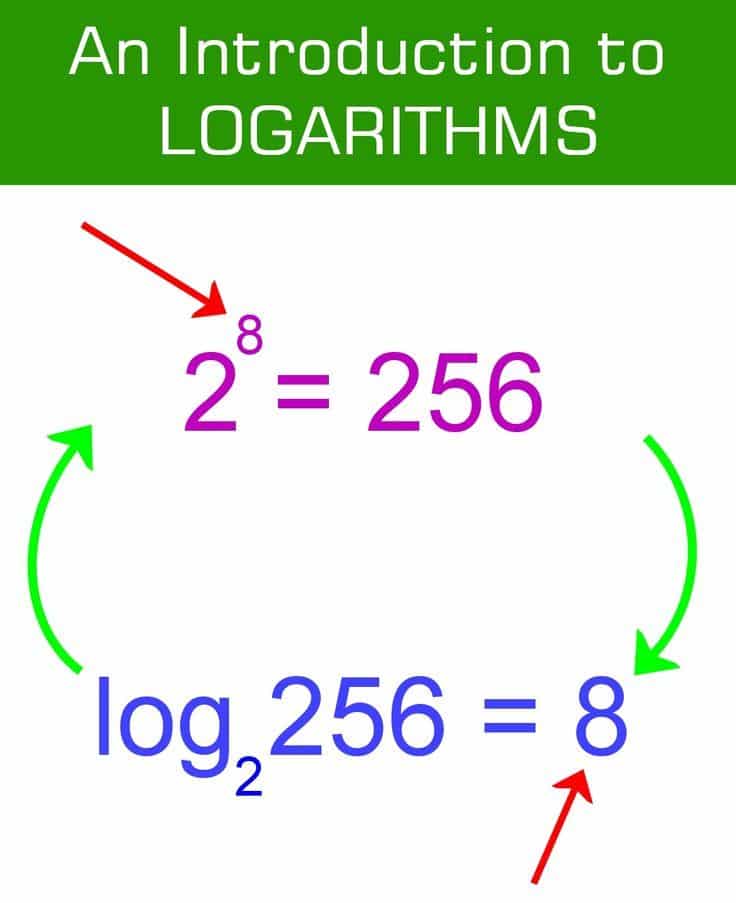
Confused by the logarithms? Don’t worry! A logarithm is actually just an exponent in a different form. The important thing to understand about logarithms is why we use them, which is to solve equations where our variable is in the exponent and we can’t get like bases. XResearch source
logax = y is the same as ay = x.
Some Properties Of Logarithms
We often need to evaluate logarithms using a base other than 10 or e. To find a way to utilize the common or natural logarithm functions to evaluate expressions like log2, we need some additional properties.
Properties of logs: Exponential Property
The exponent property allows us to find a method for changing the base of a logarithmic expression.
Properties of Logs: Change of Base
To show why these properties are true, we offer proofs.
Inverses Of Other Exponential Functions
Exponentiation occurs in many areas of mathematics and its inverse function is often referred to as the logarithm. For example, the logarithm of a matrix is the inverse function of the matrix exponential. Another example is the p-adic logarithm, the inverse function of the p-adic exponential. Both are defined via Taylor series analogous to the real case. In the context of differential geometry, the exponential map maps the tangent space at a point of a manifold to a neighborhood of that point. Its inverse is also called the logarithmic map.
In the context of finite groups exponentiation is given by repeatedly multiplying one group element b with itself. The discrete logarithm is the integer n solving the equation
- b , =x,}
where x is an element of the group. Carrying out the exponentiation can be done efficiently, but the discrete logarithm is believed to be very hard to calculate in some groups. This asymmetry has important applications in public key cryptography, such as for example in the DiffieâHellman key exchange, a routine that allows secure exchanges of cryptographic keys over unsecured information channels.Zech’s logarithm is related to the discrete logarithm in the multiplicative group of non-zero elements of a finite field.
Recommended Reading: What Is Job’s Method In Chemistry
Using Logarithms In The Real World
Logarithms are everywhere. Ever use the following phrases?
- Order of magnitude
You’re describing numbers in terms of their powers of 10, a logarithm. And an interest rate is the logarithm of the growth in an investment.
Surprised that logarithms are so common? Me too. Most attempts at Math In the Real World point out logarithms in some arcane formula, or pretend we’re geologists fascinated by the Richter Scale. “Scientists care about logs, and you should too. Also, can you imagine a world without zinc?”
No, no, no, no no, no no!
Math expresses concepts with notation like “ln” or “log”. Finding “math in the real world” means encountering ideas in life and seeing how they could be written with notation. Don’t look for the literal symbols! When was the last time you wrote a division sign? When was the last time you chopped up some food?
Basic Idea And Rules For Logarithms
Suggested background
The basic idea
A logarithm is the opposite of a power. In other words, if we take a logarithm of a number, we undo an exponentiation.
Let’s start with simple example. If we take the base $b=2$ and raise it to the power of $k=3$, we have the expression $2^3$. The result is some number, we’ll call it $c$, defined by $2^3=c$. We can use the rules of exponentiation to calculate that the result is$$c= 2^3 = 8.$$
Let’s say I didn’t tell you what the exponent $k$ was. Instead, I told that the base was $b=2$ and the final result of the exponentiation was $c=8$. To calculate the exponent $k$, you need to solve$$2^k = 8.$$From the above calculation, we already know that $k=3$. But, what if I changed my mind, and told you that the result of the exponentiation was $c=4$, so you need to solve $2^k=4$? Or, I could have said the result was $c=16$ or $c=1$ .
Just like we can change the base $b$ for the exponential function, we can also change the base $b$ for the logarithmic function. The logarithm with base $b$ is defined so that$$\log_b c = k$$is the solution to the problem $$b^k=c$$for any given number $c$ and any base $b$.
Basic rules for logarithms
Since taking a logarithm is the opposite of exponentiation , we can derive the basic rules for logarithms from the basic rules for exponents.
| Rule or special case |
|---|
| $\ln=-\ln$ |
The product rule
The quotient rule
Log of a power
Log of $e$
Log of one
Log of reciprocal
Don’t Miss: Simplifying Rational Expressions Practice Algebra 2
Rules Or Laws Of Logarithms:
As you know, a logarithm is a mathematical operation that is the inverse of exponentiation. It is expressed by using the abbreviation “log”. Before getting into solving logarithmic equations, there are several strategies and “rules” that we must first familiarize ourselves with.
First of all, in order to solve logarithmic equations, just like with polynomials, you should be comfortable graphing logarithmic functions. Check out our video on graphing logarithmic functions for an overview if needed. Also, before we get into logarithm rules, it is important that you also understand one of the simplest logarithm strategies the change of base formula. Again, check out our video on the change of base formula if you need a refresher. Now that you have all that mastered, let’s take a look at some of the most important logarithm rules:
1) Logarithm Product Rule
In general, the product rule of logarithms is defined by:
Both of these cases are always true, regardless of the base. Also, in case it comes up, the first special case is sometimes referred to as the logarithmic zero rule.
All of these rules, taken together, are extremely powerful tools we can use to solve any logarithmic problem. For a video review of these concepts, check out our videos on properties of logarithms and the quotient rule for logarithms. Now that we’ve covered the essentials, let’s get to how to solve log problems!
Logarithm Tables Slide Rules And Historical Applications
By simplifying difficult calculations before calculators and computers became available, logarithms contributed to the advance of science, especially astronomy. They were critical to advances in surveying, celestial navigation, and other domains. Pierre-Simon Laplace called logarithms
- “…n admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations.”
As the function f = bx is the inverse function of logbx, it has been called an antilogarithm. Nowadays, this function is more commonly called an exponential function.
Also Check: Introduction To Linear Algebra Fifth Edition Solutions
Logarithms And Logarithmic Functions
In this section you will learn
Common And Natural Logarithms
The common log is the logarithm with base 10, and is typically written \\) and sometimes like \\). If the base is not indicated in the log function, then the base b used is \.
The natural log is the logarithm with base \, and is typically written \\).
Note that for any other base b, other than 10, the base must be indicated in the notation \\).
Example \
Solution
a. Using the LOG key on the calculator to evaluate logarithms in base 10, we evaluate LOG
Answer: \
b. Using the LN key on the calculator to evaluate natural logarithms, we evaluate LN
Answer: \
You May Like: What Does Demographic Mean In Geography
Change Of Base Formula
One dilemma is that your calculator only has logarithms for two bases on it. Base 10 and base e . What is to happen if you want to know the logarithm for some other base? Are you out of luck?
No. There is a change of base formula for converting between different bases. To find the log base a, where a is presumably some number other than 10 or e, otherwise you would just use the calculator,
Take the log of the argument divided by the log of the base.
loga x = /
There is no need that either base 10 or base e be used, but since those are the two you have on your calculator, those are probably the two that you’re going to use the most. I prefer the natural log . The base that you use doesn’t matter, only that you use the same base for both the numeratorand the denominator.
loga x = / = /
Example: log3 7 = /
Ok Ok We Get It: What Are Logarithms About
Logarithms find the cause for an effect, i.e the input for some output
A common “effect” is seeing something grow, like going from \$100 to \$150 in 5 years. How did this happen? We’re not sure, but the logarithm finds a possible cause: A continuous return of ln / 5 = 8.1% would account for that change. It might not be the actual cause , but it’s a smooth average we can compare to other changes.
- 100 is 10 which grew by itself for 2 time periods
- 1000 is 10 which grew by itself for 3 time periods
We can think of numbers as outputs and inputs . So,
1000 outputs > 100 outputs
Why is this useful?
Logarithms put numbers on a human-friendly scale.
Large numbers break our brains. Millions and trillions are “really big” even though a million seconds is 12 days and a trillion seconds is 30,000 years. It’s the difference between an American vacation year and the entirety of human civilization.
The trick to overcoming “huge number blindness” is to write numbers in terms of “inputs” . This smaller scale is much easier to grasp:
- power of 0 = $10^0$ = 1
- power of 1 = $10^1$ = 10
- power of 3 = $10^3$ = thousand
- power of 6 = $10^6$ = million
- power of 9 = $10^9$ = billion
- power of 12 = $10^12$ = trillion
- power of 23 = $10^23$ = number of molecules in a dozen grams of carbon
- power of 80 = $10^80$ = number of molecules in the universe
A 0 to 80 scale took us from a single item to the number of things in the universe. Not too shabby.
Logarithms count multiplication as steps
Don’t Miss: Geometry Nation Section 1 Test Yourself Answers
Probability Theory And Statistics
Logarithms arise in probability theory: the law of large numbers dictates that, for a fair coin, as the number of coin-tosses increases to infinity, the observed proportion of heads approaches one-half. The fluctuations of this proportion about one-half are described by the law of the iterated logarithm.
Logarithms also occur in log-normal distributions. When the logarithm of a random variable has a normal distribution, the variable is said to have a log-normal distribution. Log-normal distributions are encountered in many fields, wherever a variable is formed as the product of many independent positive random variables, for example in the study of turbulence.
Logarithms are used for maximum-likelihood estimation of parametric statistical models. For such a model, the likelihood function depends on at least one parameter that must be estimated. A maximum of the likelihood function occurs at the same parameter-value as a maximum of the logarithm of the likelihood , because the logarithm is an increasing function. The log-likelihood is easier to maximize, especially for the multiplied likelihoods for independent random variables.
The logarithm transformation is a type of data transformation used to bring the empirical distribution closer to the assumed one.
How To Calculate Logarithms
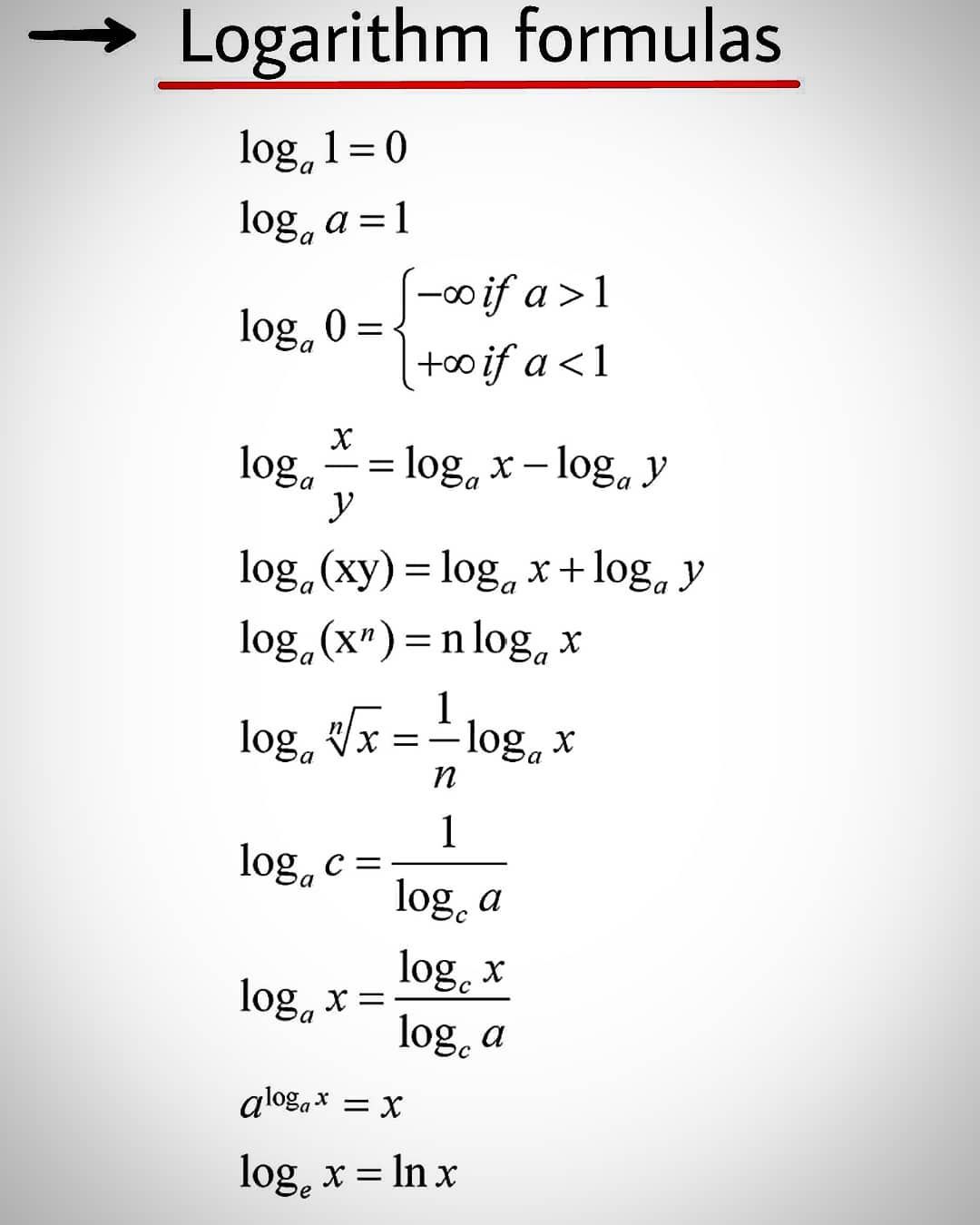
In this article, all logarithms and exponents are to base 10, and decimal answers are rounded appropriately.
The logarithm of a number is the power to which 10 must be raised to equal that number. Some simple examples:
These are commonly used in Mathematics but rarely in mental calculation. However the method described here is used for a method of calculating difficult roots and powers.
You May Like: What Does Colonialism Mean In Geography
Types Of Logarithmic Equations
- The first type looks like this.
If you have a single logarithm on each side of the equation having the same base, you can set the arguments equal to each other and then solve. The arguments here are the algebraic expressions represented by \colorM and \colorN.
- The second type looks like this.
If you have a single logarithm on one side of the equation, you can express it as an exponential equation and solve it.
Lets learn how to solve logarithmic equations by going over some examples.
Read A Brief Summary Of This Topic
logarithm, the exponent or power to which a base must be raised to yield a given number. Expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = logb n. For example, 23 = 8 therefore, 3 is the logarithm of 8 to base 2, or 3 = log2 8. In the same fashion, since 102 = 100, then 2 = log10 100. Logarithms of the latter sort are called common, or Briggsian, logarithms and are written simply log n.
Invented in the 17th century to speed up calculations, logarithms vastly reduced the time required for multiplying numbers with many digits. They were basic in numerical work for more than 300 years, until the perfection of mechanical calculating machines in the late 19th century and computers in the 20th century rendered them obsolete for large-scale computations. The natural logarithm , however, continues to be one of the most useful functions in mathematics, with applications to mathematical models throughout the physical and biological sciences.
Don’t Miss: Math Poems For High School Algebra
What On Earth Is A Logarithm
To understand what a logarithm is you first have to understand what a power is. Follow that link first if you don’t!
OK, you do know what a power is. So it makes sense to you to write something like
bx = y.
In the preceding equation, the x should look like a superscript of b. If it does not you have an underpowered browser.
After these preliminaries, we can now get into the meat of the matter. The equation is the key to everything. The number b is the base, the number x the exponent, and the expression that equals y is a power. If we think ofx as the independent variable and y as the dependent variable then defines an exponential function.
In the equation we can now pretend that two of the variables are given, and solve for the third. If the base and the exponent are given we compute a power, if the the exponent and the power are given we compute a root , and, if the power and the base are given, we compute a logarithm.
In other words, The logarithm of a number y with respect to a base b is the exponent to which we have to raise b to obtain y.
We can write this definition as
x = logby < ---> bx = y
and we say that x is the logarithm of y with base b if and only if b to the powerx equals y.
Let’s illustrate this definition with a few examples. If you have difficulties with any of these powers go back to my page on powers.
-
102 = 100 log10100 = 2
-
21/2 = 1.4142135623... log21.414.. = 1/2
Product Quotient Power And Root
The logarithm of a product is the sum of the logarithms of the numbers being multiplied the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of the p-th power of a number is p times the logarithm of the number itself the logarithm of a p-th root is the logarithm of the number divided by p. The following table lists these identities with examples. Each of the identities can be derived after substitution of the logarithm definitions x
- =\log _10+\log _x=1+\log _x.\ }
Thus, log10 is related to the number of of a positive integer x: the number of digits is the smallest integer strictly bigger than log10. For example, log10 is approximately 3.15. The next integer is 4, which is the number of digits of 1430. Both the natural logarithm and the logarithm to base two are used in information theory, corresponding to the use of nats or bits as the fundamental units of information, respectively. Binary logarithms are also used in computer science, where the binary system is ubiquitous in music theory, where a pitch ratio of two is ubiquitous and the number of cents between any two pitches is the binary logarithm, times 1200, of their ratio and in to measure exposure values, light levels, exposure times, apertures, and film speeds in “stops”.
| Base b |
|---|
Recommended Reading: How Did Geography Influence Byzantine Trade
How To Tackle Mcat Style Logarithm Questions
June 8, 2014 By Leah4sci
When it comes to mathematical calculations on the MCAT shortcuts are the way to go. But with most shortcut you have the option of falling back on the long yet proven pen-and-paper calculations to get your results.
But this is not the case when it comes to logarithms. Logs or negative logs, unlike multiplication, division and similar cannot be solved in a simple written out manner.
Therefore, learning a non-calculator trick for solving log questions is a must for every MCAT student. And that’s why my newest video shows you how to quickly tackle simple negative log questions, and a trick for solving the more difficult questions, all without a calculator.