What Is Analytical Geometry
Analytical geometry is an important branch of math, which helps in presenting the geometric figures in a two-dimensional plane and to learn the properties of these figures. Here we shall try to know about the coordinate plane and the coordinates of a point, to gain an initial understanding of Analytical geometry.
Examples Of Coordinate Geometry In A Sentence
coordinate geometry Quanta Magazinecoordinate geometryQuanta Magazine
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘coordinate geometry.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Faqs On Coordinate Geometry
1. Why do we need coordinate geometry?
Coordinate geometry has various applications in real life. Some places where we use coordinate geometry is in integration, in digital devices such as mobiles, computes, in aviation to determine the position and location of airplane accurately in GPS, and to map the geographical locations using longitudes and latitudes.
2. Who is the father of Coordinate Geometry?
The father of coordinate geometry is Rene Descartes.
3. What is the name of horizontal and vertical lines that are drawn to find out the position of any point in the Cartesian plane?
The name of horizontal and vertical lines that are drawn to find out the position of any point in the Cartesian plane is determined by the x-axis and y-axis respectively.
4. What is Abscissa and Ordinates in Coordinate Geometry?
Abscissa and Ordinates are used to identify the position of a point on the graph. The horizontal value or x-axis is called the abscissa and the vertical line or the y-axis is called the ordinate. For example, in an ordered pair , 2 is abscissa and 8 is ordinate.
Recommended Reading: Definition Of Abiotic In Biology
Examples Of Coordinate In A Sentence
coordinatingcoordinatecoordinatecoordinatecoordinatecoordinatingcoordinatescoordinatecoordinate alcoordinate Quanta Magazinecoordinate baltimoresun.comcoordinate Quanta Magazinecoordinate BostonGlobe.comcoordinate National Reviewcoordinate WSJcoordinate chicagotribune.comcoordinate baltimoresun.com/maryland/carrollcoordinate The Courier-Journalcoordinate The Atlanticcoordinate Dallas Newscoordinate The Christian Science Monitorcoordinate Washington Postcoordinate New York Timescoordinate Star Tribunecoordinate Harper’s Magazinecoordinate The Indianapolis Starcoordinate Forbescoordinate alcoordinate BostonGlobe.comcoordinate oregonlivecoordinate Scientific Americancoordinate baltimoresun.com/maryland/carroll
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘coordinate.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Analytical Geometry Formulas In A Coordinate Plane

The formulas of coordinate geometry help in conveniently proving the various properties of lines and figures represented in the coordinate axes. The important formulas of coordinate geometry are the distance formula, slope formula, midpoint formula, and section formula. Let us know more about each of the formulas in the below paragraphs.
You May Like: What Is Copulation In Biology
Coordinates Of A Point
A coordinate is an address, which helps to locate a point in space.;For a two-dimensional space, the coordinates of a point are .;Here let us take note of these two important terms.
- Abscissa:;It is the x;value in the point;, and is the distance of this point along the x-axis, from the origin
- Ordinate:; It is the y;value in the point;., and is the perpendicular distance of the point from the x-axis, which is parallel to the y-axis.
The coordinates of a point are useful;to perform numerous operations of finding distance, midpoint, the slope of a line, equation of a line.
Moving On A Coordinate Plane
René’s mouche domestique, living in a mathematician’s house, was clearly mathematically inclined and always walked in straight lines. Being a fly, it also tended to move a bit erratically, taking two steps backward for every one step forward. It had a sense of negative numbers, like this:
La mouche de René might start out at 0, move to +1, then return to -1. Next la petite mouche starts at -1, advances to 0, and backs up to -2.
But what if the fly turns 90° and heads off in a different direction? We need another number line, perpendicular to our first number line, to chart her motion. We line up the 0 on each number line, and can now measure her movement in two directions.
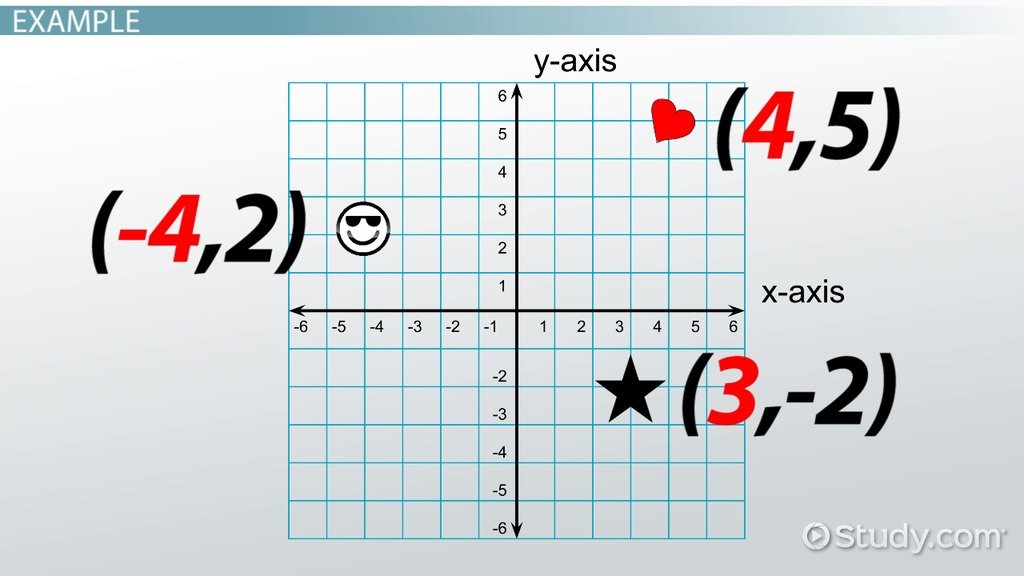
To clearly describe the fly’s movement, we need to decide which direction we will mention first, and which we will mention second. Each number line is an axis, with the x-axis going left to right and the y-axis going up to down.
The x-axis value is always given first, followed by the y-axis value. For example, the center of our number lines is , and two steps to the left is . Those x and y values form a coordinate pair, which points to a unique position on the coordinate plane.
If we wanted to be imprecise, we could roughly estimate movement with just the two intersecting, perpendicular number lines. Mathematicians are not fond of imprecision, though, so we use multiple number lines in both directions:
You May Like: How To Use Elimination In Math
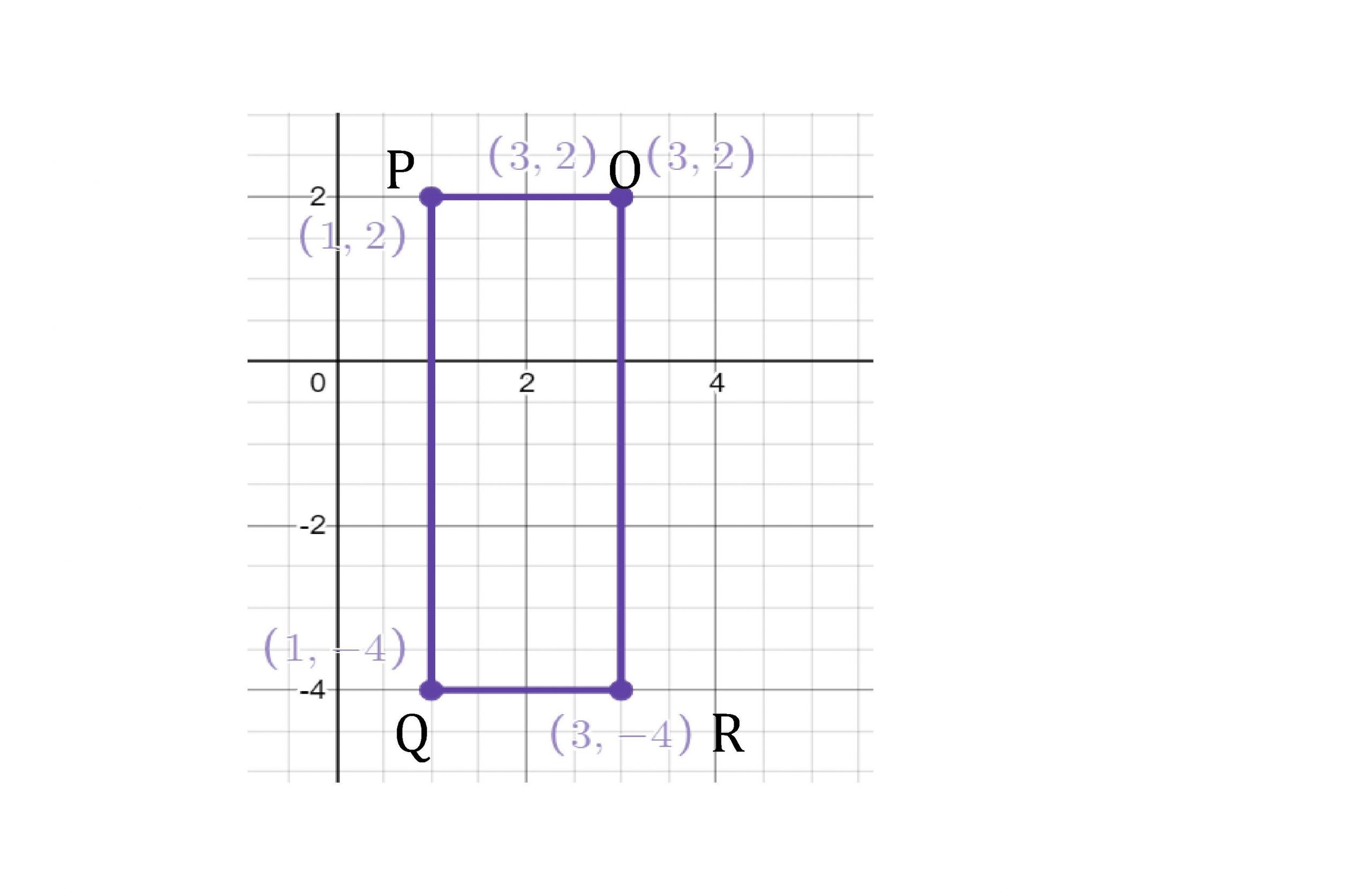
Plotting A Point In The Coordinate Plane
In this section, we are going to learn how to plot a point on the coordinate plane. Let’s take the example of point P = . To plot a point in the coordinate plane, follow the steps given below:
- Step 1: Draw two perpendiculars, the X-axis and Y-axis.
- Step 2: Start from the origin. Move 5 units to the right, along the positive X-axis.
- Step 3: Move 6 units up, along the positive Y-axis.
- Step 4: Mark the point of intersection. Mark it as .
Note that P is in the first quadrant. Also, this is known as the positive coordinate plane as the value of both the coordinates for any point in this quadrant will be positive.
Important Points on Coordinate Plane:
- The first quadrant known as the positive coordinates quadrant, is represented by the Roman numeral I.
- The second quadrant is represented by the Roman numeral II.
- The third quadrant is represented by the Roman numeral III.
- The fourth quadrant is represented by the Roman numeral IV.
- The coordinates of any point are enclosed in brackets.
Try to Solve this Challenging Question:
Find out any three points that lie in the positive coordinate plane and for which the abscissa and ordinate are equal and non-negative.
Topics Related to Coordinate Plane
Example 1: Let’s help Olivia and Jane plot the following points in the Cartesian plane:
A and C are in the first quadrant.B is in the second quadrant.D is in the fourth quadrant.
The Slope Of A Line In Coordinate Plane:
Consider the line segment joining two points \\) and \\)
From the below figure,
\ and \
The tangent of the angle gives the slope of the line.;
In the triangle \ \
Generally, the slope of the line is represented by \
Therefore, the slope of the line passing through two points \\) and \\) is given by
Don’t Miss: Elimination Method Steps
Area Of A Triangle Formed By Joining Three Points
The area of the triangle whose vertices are \,\) and \\) is
\~ + ~x_2~ +~ x_3|\)
If the area of a triangle whose vertices are \,\) and \\) is zero, then the three points are collinear.
We have learnt about two-dimensional coordinate geometry until now.;To solve more problems on topic Coordinate Geometry visit BYJUS which provides detailed and step by step solutions to all questions in an NCERT Books. Also, take free tests to practice for exams.
| MATHS Related Links |
Introduction To Coordinate Geometry
Coordinate geometry is defined as the study of geometry using the coordinate points. Using coordinate geometry, it is possible to find the distance between two points, dividing lines in m:n ratio, finding the mid-point of a line, calculating the area of a triangle in the Cartesian plane, etc. There are certain terms in Cartesian geometry that should be properly understood. These terms include:
| Coordinate Geometry Terms | |
|---|---|
| Coordinate Geometry Definition | It is one of the branches of geometry where the position of a point is defined using coordinates. |
| What are the Coordinates? | Coordinates are a set of;values which helps to show the exact position of a point in the coordinate plane. |
| Coordinate Plane Meaning | A coordinate plane is a 2D plane which is formed by the intersection of two perpendicular lines known as the x-axis and y-axis. |
| Distance Formula | |
| It is used to;divide any line into two parts, in m:n ratio | |
| Mid-Point Theorem | This formula is used to find the coordinates at which a line is divided into two equal halves. |
Read Also: What Is The Molecular Geometry Of Ccl4
Spatial Reference And Coordinate Systems
Spatial reference defines the measurement system used to locate the geometry on a model of the Earth. For people that are new to GIS, this may come as a surprise, there are several such models to represent Earth. These models are a mathematical approximations of Earth and as such, each model is designed to suit a specific purpose – such as for navigation, area calculation, large area display etc. ArcGIS supports over a thousand such systems, called coordinate systems or coordinate reference systems.
When spatial data is created, it is often specified with a spatial reference in the form a particular coordinate system. Most spatial references fall into one of two categories – geographic coordinate systems and projected coordinate systems. To integrate spatial data from various sources, the data must be transformed to a common coordinate system. Thus spatial reference system must be clearly defined not only to verify the integrity of geometric calculations between shapes, but also to allow transformations to take place between shapes in different coordinate systems.
Coordinate Geometry In Three Dimensions
Coordinate geometry is not limited to two dimensions! It is also possible to consider objects in three dimensional and even higher dimensions.
The coordinates represent a point in three-dimensional space found by moving x units along the horizontal axis, y units along the vertical axis, and z units along a third axis.
Volume is an example of how we can use coordinate geometry in three dimensions.
Don’t Miss: Span Definition Linear Algebra
How To Find Equation Of A Line In Coordinate Geometry
This equation of a line represents all the points on the line, with the help of a simple linear equation. The standard form of the equation of a line is ax + by + c= 0. There are different methods to find the equation of a line. Another important form of the equation of a line is the slope-intercept form of the equation of a line .; Here m is the slope of the line and c is the y-intercept of the line. Further, the other forms of equations of a line such as;point-slope form, two-point form,;intercept form, and the normal form,;are presented in the equation of a line webpage of cuemath.
y = mx + c
Tips And Tricks on Coordinate Geometry
Area Of A Triangle In Coordinate Geometry Example
Example: What is the area of the ABC whose vertices are A, B and C?
Solution:
A = = ;9/2;square units.
Therefore, the area of a triangle ABC is;;9/2;square units.
To know more about coordinate geometry and areas of polygons in a coordinate plane, log onto www.byjus.com. To watch interesting videos on the topic, download BYJUS The Learning App from Google Play Store.
| Also Access |
Don’t Miss: Geometry Segment Addition Postulate Worksheet
Area Of A Triangle In Coordinate Geometry
In Geometry, a triangle is a 3 sided polygon which has 3 edges and 3 vertices. Area of the triangle is a measure of the space covered by the triangle in the two-dimensional plane. In this article, let us discuss what the area of a triangle is and different methods used to find the area of a triangle in coordinate geometry.
| Also, read: |
Finding Intersections Of Geometric Objects
For two geometric objects P and Q represented by the relations P the intersection is the collection of all points ( which are in both relations.
For example, might be the circle with radius 1 and center ( +y^=1\}} and might be the circle with radius 1 and center ( } +y^=1\}} . The intersection of these two circles is the collection of points which make both equations true. Does the point ( make both equations true? Using ( +0^=1} or . On the other hand, still using ( +0^=1} or so it is not in the intersection.
The intersection of can be found by solving the simultaneous equations:
- x +y^=1}
- ( +y^=1.}
Traditional methods for finding intersections include substitution and elimination.
Substitution: Solve the first equation for y and then substitute the expression for y
- +y^=1}
- y =1-x^} .
We then substitute this value for y into the other equation and proceed to solve for x
- +=1}
- x -2x+1+1-x^=1}
Next, we place this value of x in either of the original equations and solve for y
- +y^=1}
- y
- }}}.}
So our intersection has two points:
- \;\;\mathrm \;\;\left.}
Elimination: Add a multiple of one equation to the other equation so that one of the variables is eliminated. For our current example, if we subtract the first equation from the second we get ( -x^=0} . The in the first equation is subtracted from the y in the second equation leaving no y has been eliminated. We then solve the remaining equation for x , in the same way as in the substitution method:
- x -2x+1+1-x^=1}
- +y^=1}
- y
- }}}.}
You May Like: What Is The Molecular Geometry Of Ccl4
Coordinate Geometry In Two Dimensional Plane
In coordinate geometry, first, we learn about locating the points in a Cartesian plane.
For example, the point is 3 units away from the Xaxis measured along the positive Yaxis and 2 units away from Yaxis measured along the positive Xaxis.
The points having x-coordinate as 0 lie on the Yaxis and points having y-coordinate as 0 lie on the Xaxis.
For example, the points , lie on Xaxis and the points , lie on Yaxis.
Coordinate Lines/curves And Planes/surfaces
In two dimensions, if one of the coordinates in a point coordinate system is held constant and the other coordinate is allowed to vary, then the resulting curve is called a coordinate curve. In the Cartesian coordinate system the coordinate curves are, in fact, straight lines, thus coordinate lines. Specifically, they are the lines parallel to one of the coordinate axes. For other coordinate systems the coordinates curves may be general curves. For example, the coordinate curves in polar coordinates obtained by holding r constant are the circles with center at the origin. A coordinate system for which some coordinate curves are not lines is called a curvilinear coordinate system. This procedure does not always make sense, for example there are no coordinate curves in a homogeneous coordinate system.
In three-dimensional space, if one coordinate is held constant and the other two are allowed to vary, then the resulting surface is called a coordinate surface. For example, the coordinate surfaces obtained by holding constant in the spherical coordinate system are the spheres with center at the origin. In three-dimensional space the intersection of two coordinate surfaces is a coordinate curve. In the Cartesian coordinate system we may speak of coordinate planes.
Similarly, coordinate hypersurfaces are the -dimensional spaces resulting from fixing a single coordinate of an n-dimensional coordinate system.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Section Formula In Coordinate Geometry
The section formula;is useful to find the coordinates of a point that divides;the line segment joining the points;\\) and \\) in the ratio \. The point dividing the given two points lies on the line joining the two points and;is available either between the two points or outside the line segment between the points.
\ = \left \)
How Do You Construct A Coordinate Plane
A coordinate plane can be constructed in the following manner:
- Step 1: Take a sheet of graph or grid paper.
- Step 2: Draw a horizontal line. This line is called the x-axis and is used to locate values of x.
- Step 3: Draw a vertical line. This line is called the y-axis and is used to locate values of y. To show that the axis actually
Note: To show that these axes actually go on forever in both directions, use small arrowheads at each end of the line.
Read Also: How To Use Manipulatives In Math
Coordinate Geometry Questions For Practice
Section Formula In Coordinate Geometry:
Consider two points \\) and \\) on the cartesian plane and the point \\) in the ratio \ as shown below:
In two right triangles \ and \
\ Corresponding angles )
So, by CPCT;
\ and \
\ and \
\ = n\left\) and \ = n\left\)
\ and \
\ and \
\ = m + n\) and \ = m + n\)
\ and \
Therefore, coordinates of the point \ which divides the line segment joining the points \\) and \\) in the ratio \ internally is given by
\ = \left\)
Recommended Reading: Lewis Dot Ccl4