Simplifying Rational Expressions Practice Algebra 2

Simplifying Complex Rational Expressions

A complex rational expression is a rational expression that contains additional rational expressions in the numerator, the denominator, or both. We can simplify complex rational expressions by rewriting the numerator and denominator as single rational expressions and dividing. The complex rational expression a can be simplified by rewriting the numerator as the fraction a and combining the expressions in the denominator as 1 b . We can then rewrite the expression as a multiplication problem using the reciprocal of the denominator. We get a

Given a complex rational expression, simplify it.

Begin by combining the expressions in the numerator into one expression.

Now the numerator is a single rational expression and the denominator is a single rational expression.

We can rewrite this as division, and then multiplication.

Can a complex rational expression always be simplified?

Yes. We can always rewrite a complex rational expression as a simplified rational expression.

Simplify Rational Expressions With Opposite Factors

Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. Letâs start with a numerical fraction, say 7 . We know this fraction simplifies to â1 . We also recognize that the numerator and denominator are opposites.

In Foundations, we introduced opposite notation: the opposite of a

, whose numerator and denominator are opposites, in this way:

So, in the same way, we can simplify the fraction x

In general, we could write the opposite of a

Solve Direct Variation Problems

In the following exercises, solve.

89. If \ varies directly as \ when \ and \, find \ when \.

Answer

90. If \ varies inversely as \ when \ and \ find \ when \.

91. Vanessa is traveling to see her fiancé. The distance, \, varies directly with the speed, \, she drives. If she travels 258 miles driving 60 mph, how far would she travel going 70 mph?

Answer

301 mph

92. If the cost of a pizza varies directly with its diameter, and if an 8â diameter pizza costs $12, how much would a 6â diameter pizza cost?

93. The distance to stop a car varies directly with the square of its speed. It takes 200 feet to stop a car going 50 mph. How many feet would it take to stop a car going 60 mph?

Answer

Don’t Miss: How To Think Straight About Psychology

Solve Similar Figure Applications

In the following exercises, solve.

77. \ is similar to \. The lengths of two sides of each triangle are given in the figure. Find the lengths of the third sides.

Answer

78. On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the figure below. If the actual distance from Rome to Vienna is 700 miles, find the distance from

79. Francesca is 5.75 feet tall. Late one afternoon, her shadow was 8 feet long. At the same time, the shadow of a nearby tree was 32 feet long. Find the height of the tree.

Answer

23 feet

80. The height of a lighthouse in Pensacola, Florida is 150 feet. Standing next to the statue, 5.5-foot-tall Natasha cast a 1.1-foot shadow. How long would the shadow of the lighthouse be?

Quick Link For All Rational Expressions Worksheets

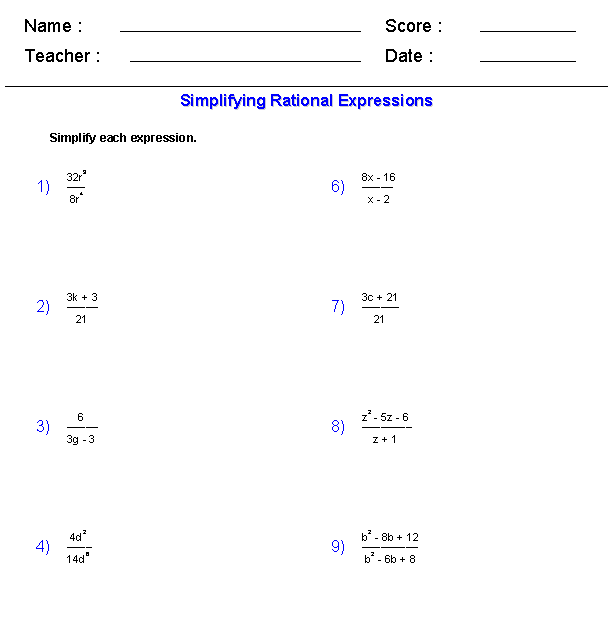
This Rational Expressions worksheet will produce problems for simplifying rational expressions. You may select the types of denominators you want in each expression. This Rational Expression worksheet will produce ten problems per page. This Rational Expressions worksheet is a good resource for students in the 9th Grade, 10th Grade, 11th Grade, and 12th Grade.

This Rational Expressions worksheet will produce problems for adding and subtracting rational expressions. You may select the types of denominators you want in each expression. This Rational Expression worksheet will produce ten problems per page. This Rational Expressions worksheet is a good resource for students in the 9th Grade, 10th Grade, 11th Grade, and 12th Grade.

This Rational Expressions worksheet will produce problems for multiplying and dividing rational expressions. You may select the types of numerators and denominators you want in each expression. This Rational Expression worksheet will produce ten problems per page. This Rational Expressions worksheet is a good resource for students in the 9th Grade, 10th Grade, 11th Grade, and 12th Grade.

This Rational Expressions worksheet will produce problems for Complex Fractions. You may select the difficulty of the problems. This Rational Expression worksheet will produce ten problems per page. This Rational Expressions worksheet is a good resource for students in the 9th Grade, 10th Grade, 11th Grade, and 12th Grade.

Also Check: What Does I Stand For In Physics

Determine The Values For Which A Rational Expression Is Undefined

When we work with a numerical fraction, it is easy to avoid dividing by zero, because we can see the number in the denominator. In order to avoid dividing by zero in a rational expression, we must not allow values of the variable that will make the denominator be zero.

If the denominator is zero, the rational expression is undefined. The numerator of a rational expression may be 0âbut not the denominator.

So before we begin any operation with a rational expression, we examine it first to find the values that would make the denominator zero. That way, when we solve a rational equation for example, we will know whether the algebraic solutions we find are allowed or not.

Solve Uniform Motion Applications

In the following exercises, solve.

81. When making the 5-hour drive home from visiting her parents, Lolo ran into bad weather. She was able to drive 176 miles while the weather was good, but then driving 10 mph slower, went 81 miles when it turned bad. How fast did she drive when the weather was bad?

Answer

45 mph

82. Mark is riding on a plane that can fly 490 miles with a tailwind of 20 mph in the same time that it can fly 350 miles against a tailwind of 20 mph. What is the speed of the plane?

83. Josue can ride his bicycle 8 mph faster than Arjun can ride his bike. It takes Luke 3 hours longer than Josue to ride 48 miles. How fast can John ride his bike?

Answer

16 mph

84. Curtis was training for a triathlon. He ran 8 kilometers and biked 32 kilometers in a total of 3 hours. His running speed was 8 kilometers per hour less than his biking speed. What was his running speed?

Don’t Miss: What Does Endpoint Mean In Geometry

Adding And Subtracting Rational Expressions

Adding and subtracting rational expressions works just like adding and subtracting numerical fractions. To add fractions, we need to find a common denominator. Letâs look at an example of fraction addition.

We have to rewrite the fractions so they share a common denominator before we are able to add. We must do the same thing when adding or subtracting rational expressions.

The easiest common denominator to use will be the least common denominator, or LCD. The LCD is the smallest multiple that the denominators have in common. To find the LCD of two rational expressions, we factor the expressions and multiply all of the distinct factors. For instance, if the factored denominators were .

Once we find the LCD, we need to multiply each expression by the form of 1 that will change the denominator to the LCD. We would need to multiply the expression with a denominator of ( and the expression with a denominator of (

Given two rational expressions, add or subtract them.

First, we have to find the LCD. In this case, the LCD will be x We then multiply each expression by the appropriate form of 1 to obtain x as the denominator for each fraction.

Now that the expressions have the same denominator, we simply add the numerators to find the sum.

How Do You Simplify Rational Expressions

Affiliate

To simplify rational expressions, first completely factor the polynomials in the numerator and the denominator. If there are any factors that are common to the numerator and denominator , cancel off these factors.

Depending on the class and the context, you might be expected to take whatever is left and multiply it back together. At this stage, though, leaving things factored is probably fine. When you get to adding rational expressions, you’ll probably multiply out the numerators, but leave the denominators factored. This is becuase, once you have a common denominator, you’ll be adding the numerators, so it will be helpful to have added terms, rather than multiplied factors, when doing that addition.

• Simplify the following expression:

To simplify a numerical fraction, I would cancel off any common numerical factors. For this rational expression , I can similarly cancel off any common numerical or variable factors.

The numerator factors as the denominator factors as . Anything divided by itself is just 1, so I can cross out any factors common to both the numerator and the denominator.

Considering the factors in this particular fraction, I get:

Then the simplified form of the expression is:

Content Continues Below

• Simplify the following rational expression:

How nice! This one is already factored for me!

The only common factor here is “x + 3″, so I’ll cancel that off and get:

Then the simplified form is:

Affiliate

You can only cancel off factors , not terms .

Also Check: Algebra 2 Chapter 1 Test Answers

You Can Only Cancel Factors Not Terms

You can use the Mathway widget below to practice finding the domain of rational functions. Try the entered exercise, or type in your own exercise. Then click the button and select “Find the Domain” to compare your answer to Mathway’s.

Please in order to enable this widget.

There is one technical consideration which is often overlooked in algebra, but crops up later in calculus. In the exercise above, when I went from the original expression:

…to the simplified form:

…I removed a “division by zero” problem. That is, in the original fraction, I could not have plugged in the value x = 3, because this would have caused division by zero.

Affiliate

But in the reduced fraction, x was allowed to be 3. So the question is, if the two expressions have different domains, can they really be equal?

No, they’re not exactly equal. To be exactly equal, they must have the same domains .

Depended upon the text you’re using, this technicality with the domain may be ignored or glossed over, or else you may be required to make note of it. Specifically, many textbooks will accept the following as your answer:

…but some books will require that your simplified form be adjusted, as necessary, in order to have the same domain as the original form, so the technically-complete answer would be:

Depending on your book and instructor, you may not need the “as long as x isn’t equal to 3″ part. If you’re not sure which answer your instructor is expecting, ask now, before the next test.

Simplify A Complex Rational Expression By Using The Lcd

We ââ¬Åclearedââ¬ï¿½ the fractions by multiplying by the LCD when we solved equations with fractions. We can use that strategy here to simplify complex rational expressions. We will multiply the numerator and denominator by the LCD of all the rational expressions.

Letââ¬â¢s look at the complex rational expression we simplified one way in Example 7.25. We will simplify it here by multiplying the numerator and denominator by the LCD. When we multiply by LCD we are multiplying by 1, so the value stays the same.

Read Also: What Is Behavioral Perspective In Psychology

Solve Applications Using Proportions

In the following exercises, solve.

75. Rachael had a 21-ounce strawberry shake that has 739 calories. How many calories are there in a 32-ounce shake?

Answer

1161 calories

76. Leo went to Mexico over Christmas break and changed $525 dollars into Mexican pesos. At that time, the exchange rate had $1 US is equal to 16.25 Mexican pesos. How many Mexican pesos did he get for his trip?

Simplifying Rational Expressions Explanation & Examples

Now that you understand what rational numbers are, the next topic to look at in this article is rational expressions and how to simplify them. Just for your own benefit, we define a rational number as a number expressed in the form of p/q where it is not equal to zero.

In other words, we can say a rational number is nothing more than a fraction in which the numerator and the denominator are integers. Examples of rational numbers are 5/7, 4/9/ 1/ 2, 0/3, 0/6 etc.

On the other hand, a rational expression is an algebraic expression of the form f / g in which the numerator or denominator are polynomials, or both the numerator and the numerator are polynomials.

Examples of rational expression are 5/x 2, 4/, /5, /, /, /2x etc.

You May Like: How To Prepare For Physics Exam

Multiply And Divide Rational Functions

19. Find \=f \cdot g\) where \=\dfrac+9 x}-3 x-4}\) and \=\dfrac-16}+12 x}\).

Answer

\=3\)

20. Find \=\dfrac\) where \=\dfrac}\) and \=\dfrac+54 x}-x-42} \).

Add and Subtract Rational Expressions with a Common Denominator

In the following exercises, perform the indicated operations.

21. \

Answer

22. \

23. \

Answer

24. \

25. \

Answer

26. \

27. \

Answer

28. \

How To

Usually, we leave the simplified rational expression in factored form. This way it is easy to check that we have removed all the common factors!

Weâll use the methods we covered in Factoring to factor the polynomials in the numerators and denominators in the following examples.

Also Check: How Are Detergents Made Chemistry