Taylor Polynomials And Taylor Series
The derivative gives the best possible linear approximation of a function at a given point, but this can be very different from the original function. One way of improving the approximation is to take a quadratic approximation. That is to say, the linearization of a real-valued function f at the point x0 is a linear polynomiala + b, and it may be possible to get a better approximation by considering a quadratic polynomial a + b + c2. Still better might be a cubic polynomial a + b + c2 + d3, and this idea can be extended to arbitrarily high degree polynomials. For each one of these polynomials, there should be a best possible choice of coefficients a, b, c, and d that makes the approximation as good as possible.
In the neighbourhood of x0, for a the best possible choice is always f, and for b the best possible choice is always f’. For c, d, and higher-degree coefficients, these coefficients are determined by higher derivatives of f. c should always be f”/2, and d should always be f”’/3!. Using these coefficients gives the Taylor polynomial of f. The Taylor polynomial of degree d is the polynomial of degree d which best approximates f, and its coefficients can be found by a generalization of the above formulas. Taylor’s theorem gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial of degree d equals f.
Determine The Values You’re Using
The first step in calculating the percentage difference involves determining the values you’re using. Remember that if you’re calculating the percentage difference, you’ll need two related values. For example, the number of sneaker sales last year compared to the number of sneaker sales this year. Since both of these concern sneaker sales, they’re related values. Once you’ve determined that your two variables are similarly related, you can proceed with your percentage difference calculation.
For example, Lets say you sold $1,000 worth of sneakers this year and you sold $800 worth of sneakers last year. 1,000 and 800 are your values.
What Is The Definition Of Integration
The process of calculating definite or indefinite integrals is known as integration. For a closed interval on the real line and some function f,
the unambiguous integral
abfdx
is the distance between the functions graph, the horizontal axis and the two vertical lines. These two lines will represent the intervals endpoints.
The term indefinite integral is used when no precise interval is given.
Well use antiderivatives to calculate the definite integral. As a result, integration is the polar opposite of differentiation.
Recommended Reading: Segment Addition Postulate Kuta
Distance And Displacement With Examples
Distance and Displacement
Distance is a scalar quantity representing the interval between two points. It is just the magnitude of the interval. However,Displacement is a vector quantity and can be defined by using distance concept. It can be defined as distance between the initial point and final point of an object. It must be the shortest interval connecting the initial and final points, that is a straight line.Let’s look at the below examples for deep understanding.
Look at the picture above, boy travels from D to A, A to B, B to C and C to D. Displacement from D to D is zero. However, distance traveled is not zero. It is equal to the perimeter of the rectangle.
Another example of distance and displacement is illustrated in Figure 1.2
John walks from the point A to B to C. What does the distance he travel? What is the displacement?
Let’s calculate first the distance that john travels. While calculating distance, we look at the numeric value of interval between traveled points. As you can see from Figure 1.2 he travels from A to B to C. Distance from A to B is 4m and B to C is 3 m. Their sum will give us total distance
4+3=7
Example: Look at the picture given below. An object moves from point A through B, C, D, E and stops at point F.
a) Find final displacement.
b) Find distance taken from point A to D.
When To Use Percentage Difference

If you need to compare two values, there are different measurements you can use. You should use the percentage difference in particular when the two values you’re measuring are related or of similar nature. Here are some instances when you can use a percentage difference:
In contrast, if you’re comparing a new value with an old value, you would be calculating the percentage change. If you’re comparing an exact value with an estimate, you would be calculating percentage error. Make sure that the values you are using align with the calculation you’re using.
Related: Learn About Being a Financial Analyst
You May Like: Mcdougal Littell Geometry Workbook Answers
What Is Percentage Difference
Percentage difference is the difference between two values divided by their average. It is used to measure the difference between two related values and is expressed as a percentage. For example, you can compare the price of a laptop this year versus the price of a laptop from last year.
It’s important not to confuse percentage difference with percentage change and percentage error. Percentage change compares an older value with a newer one while a percentage error compares a value that is exact with one that is not.
Related: 16 Accounting Jobs That Pay Well
Example Questions Using The Percentage Difference Formula
Some problems related to the percent difference formula are given below for a better understanding of this concept.
Example 1:
A shopkeeper sells mangoes for Rs. 40 per kilos. Another shopkeeper sells the same mangoes for Rs. 60 per kilos. Find out how much is the percentage difference between the selling price of the shopkeepers.
Solution:
According to the formula, first, the difference between their selling price has to be calculated which is = Rs. 20
Now, 20 needs to be divided by the average of the selling prices and multiply by 100.
Average = /2 = 50.
So, %D = × 100 = 40%.
Example 2:
Find the percentage difference between the population of two cities having 12 million and 13 million population respectively.
Solution:
Putting the values of 1.2 million and 1.3 million in the above formula, the percent difference can be calculated.
Here, difference = |12,00,000 13,00,000| = 1,00,000.
Average = = 12,50,000
%D = × 100
So, percent difference = 8%.
Example 3:
In a cricket match, one team scored 220 runs while the other team managed to score 150 runs. What is the percentage difference between their runs?
Solution:
= × 100
Read Also: Is Paris Jackson Really Michaels Daughter
Differentiation Formulas For Trigonometric Functions
Trigonometry is the concept of the relationship between angles and sides of triangles. Here, we have 6 main ratios, such as, sine, cosine, tangent, cotangent, secant and cosecant. You must have learned about basic trigonometric formulas based on these ratios. Now let us see the formulas for derivatives of trigonometric functionsand hyperbolic functions.
What Is Differentiation In Mathematics
Differentiation in Mathematics is defined as a derivative of a function in terms of an independent variable.
Let f be a function of x and y be another variable.
Here, the rate of change of y per unit change in x is denoted by dy/dx.
If the function f goes through an infinitesimal change of h near to any point x, the function is defined as,
Lim f f/ h
h tends to 0.
You May Like: Punchline Bridge To Algebra 2nd Ed Answer Key 2009
Consider The Diagram Above:
Difference between distance and displacement: If an object started travelling from B to C and ends at D, distance travelled is BC + CD. Displacement is BD.
Displacement can be ZERO: If the object started travelling from B to C to D and ends at B, distance travelled is BC + CD + DB. Displacement is ZERO.
Displacement can be NEGATIVE: If the object travels from B to A, the displacement is negative. By CONVENTION, the direction towards the right and top are positive. A way to remember: Go right = positive, go left = negative.
Difference And Comparisons Articles In Physics
To deal with a complicated subject like Physics, students must have in-depth knowledge about the concepts of various related topics. In this regard, the study in the form of difference and comparisons play a crucial role. Students can get a clear understanding of a topic and memorise intricate details about them.
As Physics holds multitudinous aspects and an ocean of topics, sub-topics and related concepts, difference and comparisons Articles in Physics can help students get comprehensive knowledge about the subject.
You May Like: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate
How To Differentiate Polynomials
This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow’s Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.There are 10 references cited in this article, which can be found at the bottom of the page. This article has been viewed 202,863 times.Learn more…
Differentiation is one of the fundamental processes in calculus. Differentiating a function ) results in another function called the derivative, written as f’ . This derivative has many uses in physics and mathematics. For instance, if we graph a polynomial f, the derivative f’ tells us the slope of the original function at all its points. The first section of this article teaches you to differentiate each term of the polynomial, one at a time. The second section uses this approach to walk through a typical example problem, differentiating an entire polynomial. After some practice, differentiating 5 will be as second nature as multiplying and dividing.
Linking Path Difference And Phase Difference: Equation
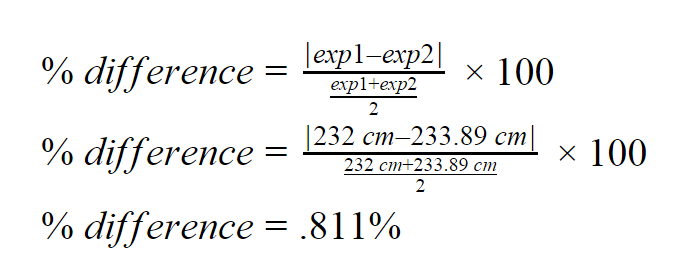
NOTE: Convert both the path difference AND the wavelength into metres first! And leave radians in terms of pi!
e.g.
a) What is the phase difference of two points of a wave of wavelength 4m that are separated by a distance of 2m?
b) What is the phase difference of two points on a wave of wavelength 12m that are separated by a distance of 3m?
c) What is the distance between two points on a wave of wavelength 20cm that are 10cm apart?
PROGRESSIVE WAVE DEFINITION:
A progressive wave distributes energy from a point source to the surrounding area. They move energy in the form of vibrating particles or fields.
Look at the animation below which shows one way that a progressive wave can be formed. Look at the green particles. Do they change their HORIZONTAL position along the wave at all?
No! They oscillate in a vertical plane, but the particles finish up in the same position that they started in after one complete cycle!
Wave Properties
It is important to be able to label various properties of a wave, and give a word definition for those properties. The video below points out the most important factors:
So, to summarise the properties of a wave:
Time period and frequency oscilloscopes
Oscilloscopes allow a wave to be traced out on a cathode ray screen. The wave form that you can see is called a trace. On an oscilloscope trace, the x axis represents time and the y axis amplitude .
b) What is the frequency of this wave?
Recommended Reading: Abiotic Meaning In Science
Derivatives Of Trigonometric Functions
We can also find the derivative of trigonometric functions that means for sin, cos, tan and so on. The formulas are given below:
- d/dx = cos x
- d/dx = -sin x
- d/dx = sec2x
- d/dx = -cosec x cot x
- d/dx = sec x tan x
- d/dx = -cosec2x
The derivative of tan x can be derived using the quotient rule as shown below:
Let f = tan x
We know that tan x = sin x/ cos x
Let us take u = sin x and v = cos x
As we know,
d/dx = / v2
d/dx = / cos2x
= /cos2x
= /cos2x
Using the identity sin2A + cos2A = 1,
= 1/cos2x
= sec2x
d/dx = sec2x
Therefore, the derivative of tan x is sec2x.
Thermodynamics And Statistical Mechanics
The first chapter of The Feynman Lectures on Physics is about the existence of atoms, which Feynman considered to be the most compact statement of physics, from which science could easily result even if all other knowledge was lost. By modeling matter as collections of hard spheres, it is possible to describe the kinetic theory of gases, upon which classical thermodynamics is based.
Thermodynamics studies the effects of changes in temperature, pressure, and volume on physical systems on the macroscopic scale, and the transfer of energy as heat. Historically, thermodynamics developed out of the desire to increase the efficiency of early steam engines.
The starting point for most thermodynamic considerations is the laws of thermodynamics, which postulate that energy can be exchanged between physical systems as heat or work. They also postulate the existence of a quantity named entropy, which can be defined for any system. In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of system and surroundings. A system is composed of particles, whose average motions define its properties, which in turn are related to one another through equations of state. Properties can be combined to express internal energy and thermodynamic potentials, which are useful for determining conditions for equilibrium and spontaneous processes.
Also Check: Core Connections Algebra Chapter 9
How To Differentiate Between Distance And Displacement
Distance is the measurement of paths taken by an object. In simple words, distance is something an object covers in a given time t. However, displacement is the shortest path taken by an object during its motion.
Distance and displacement are two physical quantities that we use in our everyday life. So, which point differentiates the two terms even if they have a common word path in them?
Also, why do we consider two different terms for the measurement of paths while considering their magnitudes? This page discusses all the differences between distance and displacement in tabular format. Also, we will go through illustrating examples on the same.
Calculus: Differentials Integrals And Partial Derivatives
Calculus differentiation, integration etc. is easier than you think. Here’s a simple example: the bucket at right integrates the flow from the tap over time. The flow is the time derivative of the water in the bucket. The basic ideas are not more difficult than that. Calculus analyses things that change, and physics is much concerned with changes. For physics, you’ll need at least some of the simplest and most important concepts from calculus. Fortunately, one can do a lot of introductory physics with just a few of the basic techniques.
So stick with us: differentiation really is just subtracting and dividing, and integration really is just multiplying and adding. This short introduction is no substitute, however, for a good high school calculus course: we shall take some short cuts of which mathematicians may disapprove.
Differential Equations: some simple examples This page supports the Physclips project.
Recommended Reading: Geometry Workbook Answers Mcgraw Hill
Derivatives In Math Calculus
The process of finding the derivative is called differentiation. The inverse process is called anti-differentiation. Lets find the derivative of a function y = f. It is the measure of the rate at which the value of y changes with respect to the change of the variable x. It is known as the derivative of the function f, with respect to the variable x.
If an infinitesimal change in x is denoted as dx, then the derivative of y with respect to x is written as dy/dx.
Here the derivative of y with respect to x is read as dy by dx or dy over dx
Example:
Let y be a dependent variable and x be an independent variable.
Consider a change in the value of x, that is dx.
This change in x will bring a change in y, let that be dy.
Now to find out the change in y with a unit change in x as follows:
Let f be a function whose value varies as the value of x varies
Steps to find the Derivative:
Now d is ignorable because it is considered to be too small.
The Root Of All Calculus
|
Contents |
Calculus or mathematical analysis is built up from 2 basic ingredients: integration and differentiation. Differentiation is concerned with things like speeds and accelerations, slopes and curves ect. These are Rates of Change, they are things that are defined locally. The Fundamental Theorem of Calculus is that Integration and Differentiation are the inverse of each other.
Recommended Reading: Parallax Errors
Quantum Mechanics Atomic Physics And Molecular Physics
Quantum mechanics is the branch of physics treating atomic and subatomic systems and their interaction based on the observation that all forms of energy are released in discrete units or bundles called “quanta“. Remarkably, quantum theory typically permits only probable or statistical calculation of the observed features of subatomic particles, understood in terms of wave functions. The Schrödinger equation plays the role in quantum mechanics that Newton’s laws and conservation of energy serve in classical mechanicsi.e., it predicts the future behavior of a dynamic systemand is a wave equation that is used to solve for wavefunctions.
For example, the light, or electromagnetic radiation emitted or absorbed by an atom has only certain frequencies , as can be seen from the line spectrum associated with the chemical element represented by that atom. The quantum theory shows that those frequencies correspond to definite energies of the light quanta, or , and result from the fact that the electrons of the atom can have only certain allowed energy values, or levels when an electron changes from one allowed level to another, a quantum of energy is emitted or absorbed whose frequency is directly proportional to the energy difference between the two levels. The further confirmed the quantization of light.
String Theory