What Is The Law Of Conservation Of Momentum In Physics

B1 Measuring Velocity With Aballistic Pendulum

Figure 3.3

A ball is shot by a spring gun into a catcher arranged to swingas a pendulum . When the ball is caught, the combinationof the ball and catcher become the bob of the pendulum. Althoughthe collision between ball and catcher is inelastic andenergy is not conserved, momentum is. With the catcherat rest, the initial momentum of the system is provided by theball, shot with velocity vb. Just after theball is caught, the momentum that is due to motion of the centerof mass of the pendulum assembled from the catcher and ball, havingvelocity vp . Conservation of momentum requiresthese be the same,

where m and M are the masses of the ball andpendulum respectively.

After the ball is caught, the energy of the combined ball andcatcher system is conserved. Initially the center of mass is ata height h1, with velocity vp. As it movesupwards against the force of gravity, the kinetic energy is convertedinto potential energy. A pawl mechanism latches it at its highestpoint, h2, where all the initial kinetic energy ofthe pendulum has been used to produce a change in the potentialenergy,

which can be determined by measuring the increase in heighth = h1 – h2 of thecenter of mass of the assembly. The value of the initial velocityof the ball is,

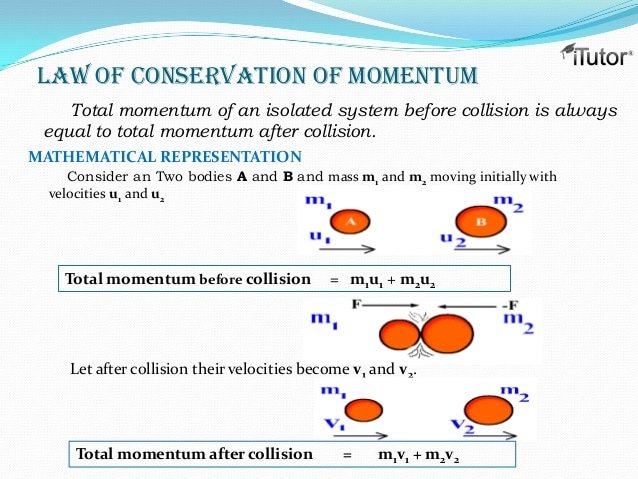
Conservation Of Linear Momentum

• Explain the meaning of âconservation of momentumâ
• Correctly identify if a system is, or is not, closed
• Define a system whose momentum is conserved
• Mathematically express conservation of momentum for a given system
• Calculate an unknown quantity using conservation of momentum

Recall Newtonâs third law: When two objects of masses m m 2 interact , the force that object 2 applies to object 1 is equal in magnitude and opposite in direction to the force that object 1 applies on object 2. Let:

• F

Then, in symbols, Newtonâs third law says

Although the magnitudes of the forces on the objects are the same, the accelerations are not, simply because the masses are different. Therefore, the changes in velocity of each object are different:

However, the products of the mass and the change of velocity are equal :

Itâs a good idea, at this point, to make sure youâre clear on the physical meaning of the derivatives in Equation 9.3. Because of the interaction, each object ends up getting its velocity changed, by an amount dv. Furthermore, the interaction occurs over a time interval dt, which means that the change of velocities also occurs over dt. This time interval is the same for each object.

Letâs assume, for the moment, that the masses of the objects do not change during the interaction. In that case, we can pull the masses inside the derivatives:

In light of this, letâs re-write Equation 9.12 in a more suggestive form:

Derivation Of Conservation Of Momentum

Newtons third law states that for a force applied by an object A on object B, object B exerts back an equal force in magnitude, but opposite in direction. This idea was used by Newton to derive the law of conservation of momentum.

Consider two colliding particles A and B whose masses are m1 and m2 with initial and final velocities as u1 and v1 of A and u2 and v2 of B. The time of contact between two particles is given as t.

Therefore, above is the equation of law of conservation of momentum where \ is the representation of total momentum of particles A and B before the collision and \ is the representation of total momentum of particles A and B after the collision.

Related Articles:

You May Like: What Causes Parallax Error And How Do You Avoid It

Application Of Law Of Conservation Of Momentum

Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?

Well, they eject matter at very high speed so in an isolated system the momentum should remain constant therefore the rocket will move in the opposite direction with the same momentum as that of the exhaust.

Stay tuned with BYJUS to know more about the law of conservation of momentum, Newtons Second Law of Motion, and much more.

Operation And Setup Of The Track:

There are several things that must be done in preparation forthe experiments. Most importantly is to check if the track islevel. Levels are provided for this purpose. Take one, and placeit over the track’s feet at one end of the track. First, placeit along the length of the track and observe the level’s “bubble”.You want this bubble to be exactly in the middle. If it is not,adjust the feet of the track by turning the screws at the baseof the feet. When the bubble is in the middle of the level, repeatthis procedure at the opposite end of the track with the levelagain length wise. Once both ends have been adjusted, repeat thisagain at both ends with the level along the width of the track.Make sure that one of the end stops is on the right end of thetrack and the launcher is on the left side of the track . For a description of the launchers see the handout. To movethe end stop and the launcher, loosen the screws on the side andslide them into position. Lastly, align the two photo gates equidistantfrom each other, making sure that the display is facing you. Thetrack is equipped with a measuring tape so that distances canbe measured. Place the first photo gate at 50cm from the launcher.Place the second photo gate at about 100cm from the launcher sothat the two photo gates are about 50cm apart.

Fig. 2

Recommended Reading: What Does Vertical Mean In Geometry

What Does Conservation Of Momentum Mean In Physics

physics is themomentum conservationmomentummomentum

. Herein, what is the conservation of momentum?

Conservation of momentum is a fundamental law of physics which states that the momentum of a system is constant if there are no external forces acting on the system. It is embodied in Newton’s first law .

Also Know, what is the formula for law of conservation of momentum? The equation for conservation of momentum looks like this: total momentum before = total momentum after. pbefore = pafter. before = after.

Simply so, what do you mean by law of conservation of momentum?

The law of conservation of momentum states that for two objects colliding in an isolated system, the total momentum before and after the collision is equal. This is because the momentum lost by one object is equal to the momentum gained by the other.

What is principle of conservation of momentum?

In physics, the principle of conservation of momentum states that when you have an isolated system with no external forces, the initial total momentum of objects before a collision equals the final total momentum of the objects after the collision.

Closed And Isolated Systems

A closed system has no transfer of matter or net force with the outside world. An isolated system has no transfer of matter, net force, or energy with the outside world. Generally, we use closed systems in physics and isolated systems in thermodynamics.

These system types are important to understand because we study momentum problems in simplified versions of reality closed and isolated systems so that we only have to keep track of momentum within the system.

In real life, closed and isolated systems do not exist. Even if an object is placed in a remote spot in the vacuum of space, there will be small gravitational forces, electromagnetic energy exchange, and even occasional gas particles interacting with it.

However, we can study physics problems in the context of these systems. We can do so because, in certain situations, the forces, matter, and energy of the outside world are negligible, that is, their effect is so small and minuscule that they can be ignored.

You May Like: Do You Capitalize Bachelor’s Degree In Psychology

Difference Between Momentum And Velocity

September 25, 2011 Posted by Admin

Momentum vs Velocity

Momentum and velocity are two very basic concepts. These two concepts have remarkable similarities, but in theory, these are two different quantities. It is crucial to have a clear understanding in both velocity and momentum in order to excel in fields such as mechanics, automobile engineering, and almost every field in physics and engineering. This article will present the definitions of the two concepts, their uses, common laws and theories regarding them, their similarities and finally their differences.

Velocity

Momentum

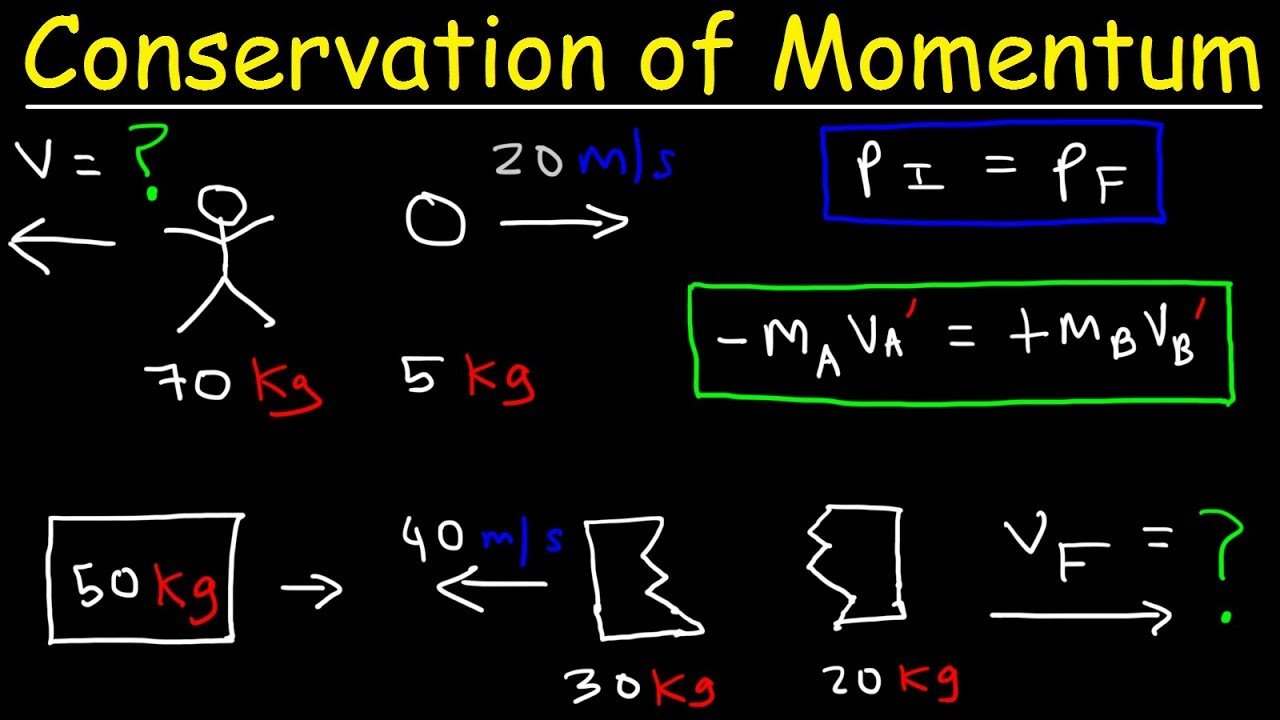
Solved Problems On Law Of Conservation Of Momentum

Q1. There are cars with masses 4 kg and 10 kg respectively that are at rest. A car having the mass 10 kg moves towards the east with a velocity of 5 m.s-1. Find the velocity of the car with mass 4 kg with respect to ground.Ans: Given,

We know from the law of conservation of momentum that,

Pinitial = 0, as the cars are at rest

Pfinal = p1 + p2

= 4 kg.v1 + 10 kg.5 m.s-1

Pi = Pf

0=4 kg.v1+50 kg.m.s-1

v1 = 12.5 m.s-1

Q2. Find the velocity of a bullet of mass 5 grams which is fired from a pistol of mass 1.5 kg. The recoil velocity of the pistol is 1.5 m.s-1.Ans: Given,

Mass of bullet, m1 = 5 gram = 0.005 kg

Mass of pistol, m2 = 1.5 kg

The velocity of a bullet, v1 = ?

Recoil velocity of pistol, v2 = 1.5 m.s-1

Using law of conservation of momentum,

m1u1 + m2u2 = m1v1 + m2v2

Here, Initial velocity of the bullet, u1 = 0

Initial recoil velocity of a pistol, u2 = 0

+ = +

0 = +

Hence, the recoil velocity of the pistol is 450 m.s-1.

Read Also: Who Is Paris Jackson’s Biological Father

Three Application Of Conservation Of Momentum In Daily Life

• Air filled balloons

In the air-filled balloon, balloon, and air inside form a kind of system. Initially when the system is at rest, so the momentum of the system is also zero. As soon as the balloon is set free air escapes out with some great velocity, balloon moves forward in the direction opposite to air rushing out.

• The system of gun and bullet

Before firing both gun and bullet are at rest, therefore momentum of the system is zero. When the bullet is fired the bullet moves forward and gun recoils back. The mass of the gun is very large as compared to the mass of the bullet, therefore the recoils velocity is very small as compared to the velocity of the bullet.

• Motion of rockets and jet engines

Rockets and jet engines also work on the law of conservation of momentum. In these hot gases produced by burning of fuel rush out with large momentum, Due to this, these machines gain an equal and opposite momentum. This momentum enables the rockets and jet engines with very high velocities.

Conservation Of Momentum Equation

The general equation for conservation of momentum during a collision between n number of objects is given as:

Where mi is the mass of object i, via is the velocity of object i before the collision, and vib is the velocity of object i after the collision.

This formula is given in summation notation, which makes it easy to equate the sum of all objects momentum before the collision to the sum of all objects momentum after the collision.

Read Also: Geometry 1.7 Worksheet Answers

The Definition Of Conservation Of Momentum

The law of conservation of momentum tells us that in closed and isolated systems, the sum of all objects momentum stays constant. This means that momentum cannot be created or destroyed, it is conserved.

Remember that the formula for the momentum of an object is given as:p = m×vWhere p is the objects momentum, m is the objects mass, and v is the objects velocity.

In a collision between two objects, the decrease in one objects momentum is equal to the increase in the other objects momentum. In fact, this transfer of momentum can happen between any number of objects within a system.

Collisions Explosions And Impulse

Momentum, kinetic energy and impulse can be used to analyse collisions between objects such as vehicles or balls. Forces and the final velocity of objects can be determined.

The symbol for momentum is \ so this can also be written as:

Momentum is measured in kg ms-1.

Momentum is a vector quantity that depends on the direction of the object. Momentum is of interest during collisions between objects.

When two objects collide the total momentum before the collision is equal to the total momentum after the collision .

This is the law of conservation of momentum. It is true for all collisions.

Also Check: How Many Subfields Of Psychology Are There

What Is Conservation Of Energy Give Two Examples

Daily life examples of Conservation of energy:

2) When a moving car hits another car which is parked to make it move, energy of the moving car is transferred from the moving car to the parked car. 3) Water is used to produce electricity. Water falls from the sky, converting potential energy to kinetic energy.

Derivation Of The Law Of Conservation Of Momentum

As per Newtons 2nd Law of motion, force F = p/t In an isolated system, the net external force is zero, F = 0Hence from equation for that isolated system we get, p/t = 0this implies, p = 0or, change in momentum is zero This means Momentum remains constant when the external force is zero or Momentum remains constant in an isolated system. Thus we can mathematically derive the law or principle of conservation of linear momentum.

In a system of particles, in which each may have different amounts of momentum, the total momentum of the system is the sum of all the individual momenta.

You May Like: What Is The Molecular Geometry Of Ccl4

Selected Solutions To Problems & Exercises

1. 0.122 m/s

3. In a collision with an identical car, momentum is conserved. Afterwards vf = 0 for both cars. The change in momentum will be the same as in the crash with the tree. However, the force on the body is not determined since the time is not known. A padded stop will reduce injurious force on body.

5. 22.4 m/s in the same direction as the original motion

• College Physics. : OpenStax College. Located at: . License: CC BY: Attribution. License Terms: Located at License

Law Of Conservation Of Momentum Definition

According to this law: The momentum of an isolated system of two or more than two interacting bodies remains constant.The momentum of a system depends on its mass and velocity. A system is a group of bodies within certain boundaries. An isolated system is a group of interacting bodies on which no external force is acting. It is expressed mathematically as:The above formula states that the momentum of two striking bodies before and after collision remains the same.

Also Check: How To Intimidate Someone Psychologically

Conservation Of Linear Momentum:

Conservation of linear momentum is based on Newtons second law of motion which states that in an isolated system the total momentum remains the same. Lets consider the following example,

Remember: In the above experiment we did not consider any loss of energy due to friction, heat, etc. and all the collisions were elastic in nature i.e. there was a total transfer of energy, Actual observations may differ.

Lets consider a case where a football of mass \ is resting on the ground, a bowling ball with a comparatively heavier mass of \ is thrown at the football at a velocity of \.

When the bowling ball hits the football the energy is transferred and the bowling ball loses some velocity and moves at a new velocity \, the football moves at velocity \, why did the football move?

To conserve linear momentum, i.e. the bowling ball had an initial momentum of \ so as \ and the momentum of football should be equal to the momentum lost by the bowling ball according to the law of conservation of momentum, the football had no other option than moving at a velocity \.

Where Does The Law Of Conservation Of Momentum Apply

Take the scenario of a snowball hitting a tree and stopping. Initially, the snowball had momentum but now neither the snowball nor tree have momentum, so momentum is lost . Or since the tree has such a large mass, is the velocity of the tree is so small that it’s hardly noticeable?

If the explanation is the latter, this wouldn’t hold for a fixed object of smaller mass. So in that case, how would the law of conservation of momentum hold?

• 3$\begingroup$To be clear: the conservation of momentum ALWAYS holds, in an incredible manner. If you will find a single exception, you’re gonna be a Nobel Laureant at least. But it says that the overall momentum is conserved, so as a check, always include the whole universe and remove all objects that are clearly not affected.$\endgroup$
• QmechanicJan 9 at 11:05
• $\begingroup$Just to stress it more, conservation of momentum is valid even in nuclear reactions – one of the smallest objects possible .$\endgroup$

Momentum is conserved only if there is no net external force on the system.

Consider the snowball and the tree as the system. In your case, the earth provides an external force on the tree, so the momentum of the snowball/tree system is not conserved. If the tree is “suspended” momentum would be conserved, but the final velocity of the tree would be very small and hardly noticeable due to its large mass.

$$m_sv_s = m_ev_e$$

where “e” stands for the earth. If you plug the numbers in, thus you get

$$v_e \approx 3.3\cdot10^\frac$$

Recommended Reading: Who Are Paris Jackson’s Biological Parents