Spherical Geometry Triangle Angle Sum Proof

Relation To Euclid’s Postulates

If “line” is taken to mean great circle, spherical geometry obeys two of Euclid’s postulates: the second postulate and the fourth postulate . However, it violates the other three. Contrary to the first postulate , there is not a unique shortest route between any two points contrary to the third postulate, a sphere does not contain circles of arbitrarily great radius and contrary to the fifth postulate, there is no point through which a line can be drawn that never intersects a given line.

A statement that is equivalent to the parallel postulate is that there exists a triangle whose angles add up to 180°. Since spherical geometry violates the parallel postulate, there exists no such triangle on the surface of a sphere. The sum of the angles of a triangle on a sphere is 180°, where f is the fraction of the sphere’s surface that is enclosed by the triangle. For any positive value of f, this exceeds 180°.

Maximum Sum Of Angles In Triangle In Sphere

Recently my differential geometry lecturer demonstrated that the sum of the interior angles of a triangle in a sphere is not necessarily never $180^\circ$. This is one way to prove that the earth is not flat. I was wondering, what then is the maximum sum of the interior angles of triangles in a sphere, since this sum is not a constant?

• 8$\begingroup$The maximal sum of interior angles is achieved by drawing a very small triangle somewhere on the sphere and then declaring the inside to be the outside and vice versa. The sum of the interior and exterior angles is necessarily always $3\times 360^\circ$ and since one of these sets cannot sum to less than $180^\circ$, the opposite one cannot be more than $5\times 180^\circ$.$\endgroup$Oct 24, 2011 at 23:52
• 3$\begingroup$The “not necessarily” in the question should be replaced by “never” .$\endgroup$Oct 25, 2011 at 0:04

Proof That The Angle Sum Of A Triangle Is Always Greater Than 180 Degrees In Elliptic Geometry

I’ve scoured the internet and have found many proofs showing that in Euclidean geometry, the angle sum of a triangle is always 180 degrees. I’ve also found many proofs showing that in hyperbolic geometry, the angle sum of a triangle is always less than 180 degrees. For some reason I have been unable to find a proof that shows that, in elliptic geometry, the angle sum of a triangle is greater than 180 degrees.

Could anyone state the proof, or even better, provide a link or book where I could read up on it?

SOLUTION – verified

Using the reading Sam suggested, combined with a book I’ve been reading, I think I’ve come up with a hybrid proof.

Definition: A lune is a wedge of a sphere with angle $\theta$, represented by L in the proof.

$\alpha$, $\beta$, and $\gamma$ are the three angles of the triangle.

Proof

If you read the page Sam suggested, especially part 3. Triangle on Spheres, it should help with the idea of lunes. The six lunes created by the angles of the triangle encompass the entire sphere as well as overlapping the triangle area in the front and rear of the sphere 4 extra times. Thus, we begin with the radius of a sphere plus 4 times the area of the triangle is equal to the 6 lunes.

$4\pi r^2 + 4 = 2L + 2L + 2L$

$2 = 2 + L + L)$

$2\pi r^2 + 2 = L + L + L$

At this point we need to use a theorem that states that a lune whose corner angle is $\theta$ radians has area $2\theta r^2$.

$2\pi r^2 + 2 = 2\alpha r^2 + 2\beta r^2 + 2\gamma r^2$

$2\pi r^2 + 2 = 2 r^2 $

You May Like: What Is Phenotype In Biology

Regular Polygons On The Sphere

Recall that a regular polygon is a polygon with all sides the same length and all angles equal. We keep the same definition in non-Euclidean geometry.

In Euclidean geometry, the angle sum for a polygon with n sides is < math> \times 180^\circ< /math> , and this forces the corner angles of a regular < math> n< /math> -gon to be < math> \frac< /math> . This means there is only one shape of Euclidean regular < math> n< /math> -gon.

In spherical geometry there are many regular < math> n< /math> -gons. There is a regular < math> n< /math> -gon with any angle sum larger than < math> \times 180^\circ< /math> . So, there is a regular < math> n< /math> -gon with any choice of corner angle larger than < math> \frac< /math> . The maximum sizes arent as important, and are left for the exercises.

This table summarizes the corner angles of some regular polygons on the sphere:

To make a regular tessellation of the sphere, we need to pick one regular polygon and use it to cover the sphere. As with regular tessellations of the plane, the difficulty is to fit corner angles around a vertex, which requires the corner angle to divide evenly into 360°. This means that the possibilities for corner angles are 360/2 = 180°, 360/3 = 120°, 360/4 = 90°, 360/5 = 72°, 360/6 = 60°, and so on.

Relation To Similar Geometries

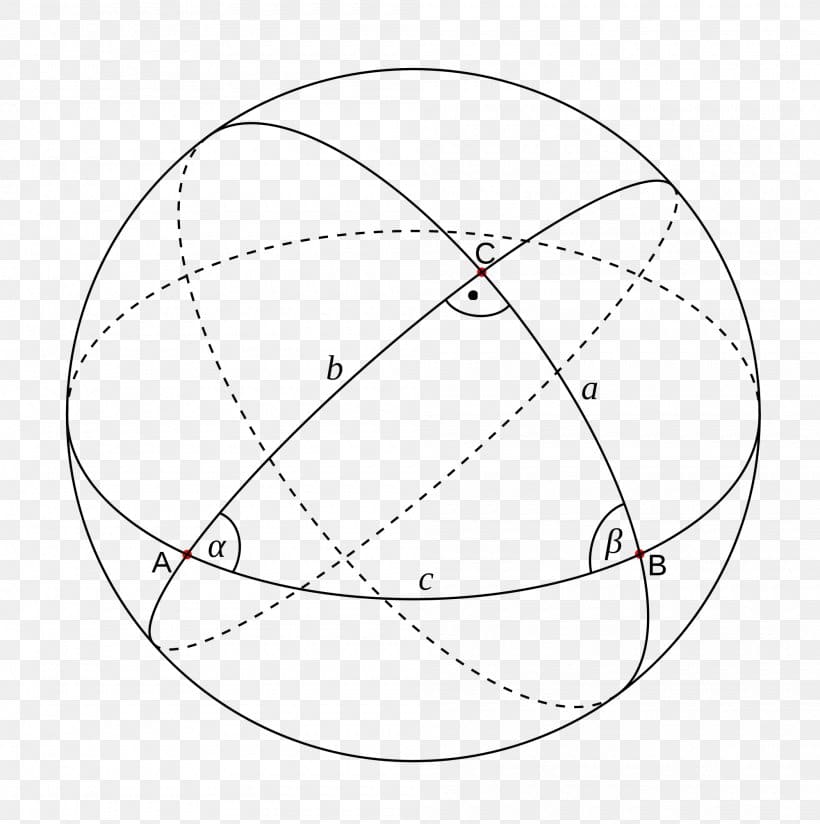
Spherical geometry is closely related to elliptic geometry.

An important geometry related to that of the sphere is that of the real projective plane it is obtained by identifying antipodal points on the sphere. Locally, the projective plane has all the properties of spherical geometry, but it has different global properties. In particular, it is non-orientable, or one-sided, and unlike the sphere it cannot be drawn as a surface in 3-dimensional space without intersecting itself.

Concepts of spherical geometry may also be applied to the oblong sphere, though minor modifications must be implemented on certain formulas.

Higher-dimensional spherical geometries exist see elliptic geometry.

Read Also: What Is Emulsion In Chemistry

The Exterior Angle Theorem

Scott E. BrodieAugust 14, 2000

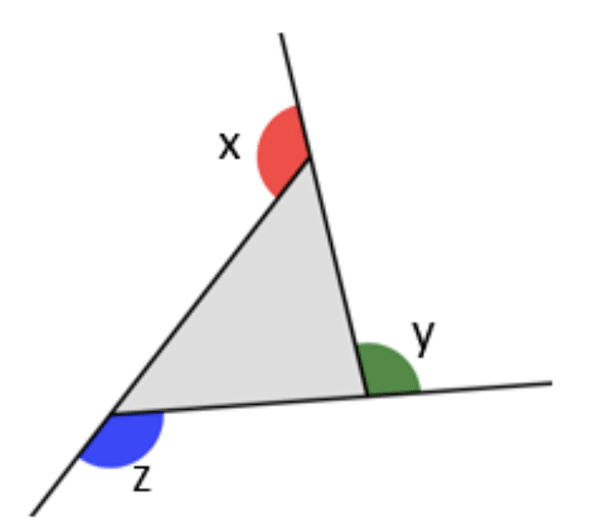
The Exterior Angle Theorem ” rel=”nofollow”> Euclid I.16), “In any triangle, if one of the sides is produced, then the exterior angle is greater than either of the interior and opposite angles,” is one of the cornerstones of elementary geometry. In many contemporary high-school texts, the Exterior Angle Theorem appears as a corollary of the famous result that the three angles of a triangle sum to two right angles — .

In contrast, in Euclid’s sequence of propositions, the Exterior Angle Theorem appears before any invocation of the Parallel Postulate. Thus the Exterior Angle Theorem, and many of its consequences, apply more generally than one might suppose from the watered-down “High School” treatment.

The importance of the Exterior Angle Theorem can be seen by listing some of the important theorems which derive directly from it:

• In any triangle, the sum of any two angles is less than two right angles

This is the beginning of the argument which leads to Legendre’sLemma: The sum of the three angles of a triangle are less than or equalto two right angles.

One can also use this proposition to simplify Euclid’s enunciation ofthe Parallel Postulate: it becomes unnecessary to state that two linescut by a transversal “meet on that side on which are the angles lessthan the two right angles.” If they met on the other side, they would forma triangle whose angle sum exceeds two right angles.

• No triangle can contain two right angles .

Napier’s Rules For Quadrantal Triangles

A quadrantal spherical triangle is defined to be a spherical triangle in which one of the sides subtends an angle of /2 radians at the centre of the sphere: on the unit sphere the side has length /2. In the case that the side c has length /2 on the unit sphere the equations governing the remaining sides and angles may be obtained by applying the rules for the right spherical triangle of the previous section to the polar triangle A’B’C’ with sides a’,b’,c’ such that A’ = a, a’ = A etc. The results are:

a

which is a relation between the six parts of the spherical triangle.

Recommended Reading: What Is Limiting Factor In Biology

Area And Spherical Excess

Consider an N-sided spherical polygon and let An denote the n-th interior angle. The area of such a polygon is given by

Area of polygon

, }\equiv E=E_=A+B+C-\pi ,}

where E is the amount by which the sum of the angles exceeds radians. The quantity E is called the spherical excess of the triangle. This theorem is named after its author, Albert Girard. An earlier proof was derived, but not published, by the English mathematician Thomas Harriot. On a sphere of radius R both of the above area expressions are multiplied by R2. The definition of the excess is independent of the radius of the sphere.

The converse result may be written as

A Area of the sphere . }}}}.}

Since the area of a triangle cannot be negative the spherical excess is always positive. It is not necessarily small, because the sum of the angles may attain 5 . For example,an octant of a sphere is a spherical triangle with three right angles, so that the excess is /2. In practical applications it is often small: for example the triangles of geodetic survey typically have a spherical excess much less than 1′ of arc. .On the Earth the excess of an equilateral triangle with sides 21.3 km is approximately 1 arc second.

There are many formulae for the excess. For example, Todhunter, gives ten examples including that of L’Huilier:

tan

Deriving The Surface Area Of A Spherical Triangle

A triangle on a sphere is composed of points $A$, $B$ and $C$.The $\alpha$, $\beta$ and $\gamma$ denote the angles at the corresponding points of the triangle:

The Girard’s theorem states that the surface area of any spherical triangle:

$$ A = R^2 \cdot E $$

where $R$ is the radius of the sphere and $E$ is the excess angle of $$

I’m wondering how to derive this formula.

Could you please help explain this clearly?

• 1$\begingroup$TeX tip: Notice the difference between $\alpha$ + $\beta$ + $\gamma$ – $\pi$ and $\alpha + \beta + \gamma – \pi$. In the former, the minus sign looks like a hyphen instead of a minus sign. There’s a reason why that’s not standard usage. I fixed this in the posting.$\endgroup$ Michael HardyFeb 16, 2012 at 18:06
• $\begingroup$@Nunoxic, no. That question is about how to determine the angles between ABC, ACB and BAC.$\endgroup$Feb 16, 2012 at 18:06
• $\begingroup$There is a nice proof at math.rice.edu/~pcmi/sphere/gos4.html$\endgroup$

Consider the following three parts of the sphere: let $P_A$ be the lune created from the triangle $ABC$ plus the triangle adjacent across the $BC$ line segment, plus the opposite lune , and similarly for parts $P_B$ and $P_C$.

The area of $P_A$ is $4\alpha R^2$: the total area of the sphere is $4\pi R^2$, and the area of $P_A$ is certainly proportional to $\alpha$.

Notice now that $P_A\cup P_B\cup P_C$ is the entire sphere, and that $P$’s intersect at the triangle + the opposite triangle. We thus have:

Don’t Miss: Scratch Geometry Dash All Levels

Maths In A Minute: Not Always 180

Over 2000 years ago the Greek mathematician Euclid came up with a list of five postulates on which he thought geometry should be built. One of them, the fifth, was equivalent to a statement we are all familiar with: that the angles in a triangle add up to 180 degrees. However, this postulate did not seem as obvious as the other four on Euclid’s list, so mathematicians attempted to deduce it from them: to show that a geometry obeying the first four postulates would necessarily obey the fifth. Their struggle continued for centuries, but in the end they failed. They found examples of geometries that do not obey the fifth postulate.

Derivation Of The Cosine Rule

The spherical cosine formulae were originally proved by elementary geometry and the planar cosine rule . He also gives a derivation using simple coordinate geometry and the planar cosine rule . The approach outlined here uses simpler vector methods.

Consider three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle . The arc BC subtends an angle of magnitude a at the centre and therefore OB·OC = cos a. Introduce a Cartesian basis with OA along the z-axis and OB in the xz-plane making an angle c with the z-axis. The vector OC projects to ON in the xy-plane and the angle between ON and the x-axis is A. Therefore, the three vectors have components:

OA OC .

The scalar product OB·OC in terms of the components is

OB·OC =\sin c\sin b\cos A+\cos c\cos b} .

Equating the two expressions for the scalar product gives

cos .

This equation can be re-arranged to give explicit expressions for the angle in terms of the sides:

cos }.}

The other cosine rules are obtained by cyclic permutations.

Don’t Miss: What Is Insolation In Geography

Notes On Spherical Trigonometry

Spherical trigonometry is the study of curved triangles, triangles drawn on the surface of a sphere. The subject is practical, for example, because we live on a sphere. The subject has numerous elegant and unexpected theorems. We give a few below.

The diagram shows the spherical triangle with vertices A, B, and C. The angles at each vertex are denoted with Greek letters , , and . The arcs forming the sides of the triangle are labeled by the lower-case form of the letter labeling the opposite vertex.

Napier’s Rules For Right Spherical Triangles

When one of the angles, say C, of a spherical triangle is equal to /2 the various identities given above are considerably simplified. There are ten identities relating three elements chosen from the set a, b, c, A, B.

Napier provided an elegant mnemonic aid for the ten independent equations: the mnemonic is called Napier’s circle or Napier’s pentagon .

First, write the six parts of the triangle in the order they occur around any circuit of the triangle: for the triangle shown above left, going clockwise starting with a gives aCbAcB. Next replace the parts that are not adjacent to C by their complements and then delete the angle C from the list. The remaining parts can then be drawn as five ordered, equal slices of a pentagram, or circle, as shown in the above figure . For any choice of three contiguous parts, one will be adjacent to two parts and opposite the other two parts. The ten Napier’s Rules are given by

• sine of the middle part = the product of the tangents of the adjacent parts
• sine of the middle part = the product of the cosines of the opposite parts

For an example, starting with the sector containing a

Read Also: What Is Atomic Radius In Chemistry

Sum Of Angles Of A Triangle On A Sphere

What is the minimum and maximum of sum of angles of a spherical triangle? Let us remove a constraint from spherical triangles: sides are not necessarily circular arcs. Then what will be the minimum and maximum of sum of angles of such triangles?

• $\begingroup$If the Earth is so big that locally it looks flat, then a triangle on the ground approximates on in the plane, with a sum of close to $180^\circ$. It can be made as close as desired by making the triangle small enough: the smaller it is the flatter the Earth looks. So that’s the smallest, except that it’s really an infimum rather than a minimum. $\qquad$$\endgroup$May 9, 2016 at 17:19
• 4$\begingroup$You really want to constraint the sides somehow. Otherwise the bounds are $0$ and $6\pi$ radians.$\endgroup$May 9, 2016 at 17:19
• 1May 9, 2016 at 17:28
• 1$\begingroup$@EricTowers Indeed, at first it seems that the upper bound is $3\pi$ but in case of no constrains one can simply draw a “triangle” with virtualy zero angle sum, and then threat the outside as an inside of a second “triangle” with an angle sum of course $6\pi$$\endgroup$May 9, 2016 at 17:35
• 1$\begingroup$Yes, for a triangle whose sides are required to be arcs of great circles, the angle-sum $\Sigma$ satisfies $\pi< \Sigma< 5\pi$. This corresponds to bounds on the area of such a triangle being $0< A< 4\pi r^2$.$\endgroup$

Symmetry Groups Of The Sphere

Symmetry groups of plane figures were completely classified into the rosette, frieze, and wallpaper groups. There are infinitely many rosette groups in two types, depending on whether reflection symmetry is present. The frieze and wallpaper groups were finite lists, harder to classify and less structured.

For the sphere, the classification of symmetry groups is closely tied to the platonic solids. In fact:

Every symmetry group of a spherical figure comes about by selecting some of the symmetries of a regular spherical tessellation.

For example, there are two symmetry groups coming from the octahedron: One which has all symmetries of the octahedron and a second which has only the rotations, and none of the reflections. Escher’s has symmetry of this reflectionless octahedron type. Two more spherical symmetry groups come from the icosahedron, in exactly the same way. Because of duality, the cube and dodecahedron contribute nothing new – they have the same symmetries as their duals. The tetrahedron contributes three: One with no reflections, one with all six possible reflections, and a third with three of the reflections.

For more details, notation, and a complete list of all these groups, see Wikipedia’s list of spherical symmetry groups.

Recommended Reading: What Is The Definition Of Mantle In Geography

Geometry Of Spherical Triangle

Using the formula for the area of a spherical triangle, find and prove a formula relating the angle sum of a spherical polygon to its area

Thought:

Area $=\mathbb^2$ where $\alpha, \beta, \gamma$ are the interior angles

Let $n$ be the number of vertices/sides of a polygon.

Consider a quadrilateral $n=4$ with interior angle $$

Area $=\mathbb^2$

then how do I induce to infinite $n$???

The natural thing seems to be the area is the sum of the angles minus $\pi$ times two less than the number of sides. You should be able to prove this by cutting the polygon into triangles.This means that in Euclidean space all polygons have zero area.

• $\begingroup$”This means that in Euclidean space all polygons have zero area.” Of course this is wrong. In spherical geometry, angle excess is proportional to area. This does not happen in euclidian geometry.$\endgroup$Mar 12, 2013 at 7:11
• 2$\begingroup$@arbautjc: true, but it is not as silly as it sounds. Euclidean geometry is like spherical geometry on an infinite radius sphere. All finite polygons have zero area relative to such a sphere.$\endgroup$ Ross MillikanMar 12, 2013 at 13:02
• $\begingroup$There is an r^2 factor which tends toward infinity, that’s why the limit is not zero.$\endgroup$

A polygon with an infinite number of vertices/sides is a circle. So, what is the area of a circle in spherical geometry? It is the surface area covered by the region on $\mathbb^2$ bounded by the curve resulting from intersecting $\mathbb^2$ with a plane.