How Do U Know If Angles Are Congruent
Two angles are congruent if they have the same measure. You already know that when two lines intersect the vertical angles formed are congruent . Well, it turns out that the bisector of an angle divides the angle into two angles , each of which has measure equal to one-half the measure of the original angle .
What Is The Difference Between Sas And Sss
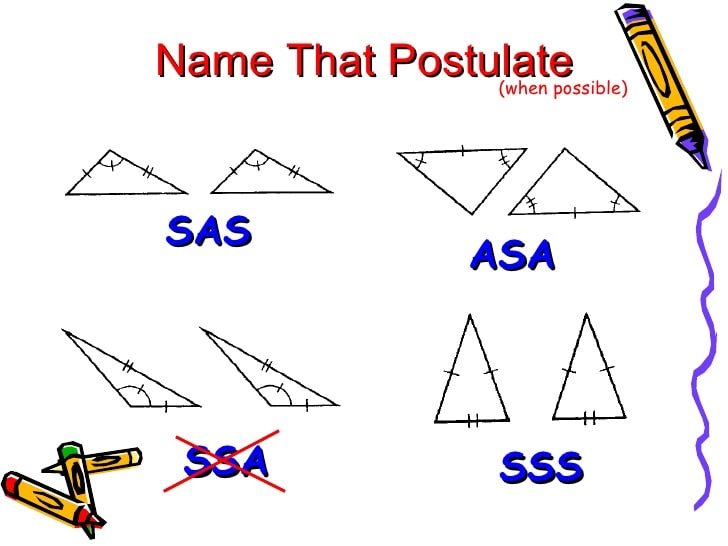
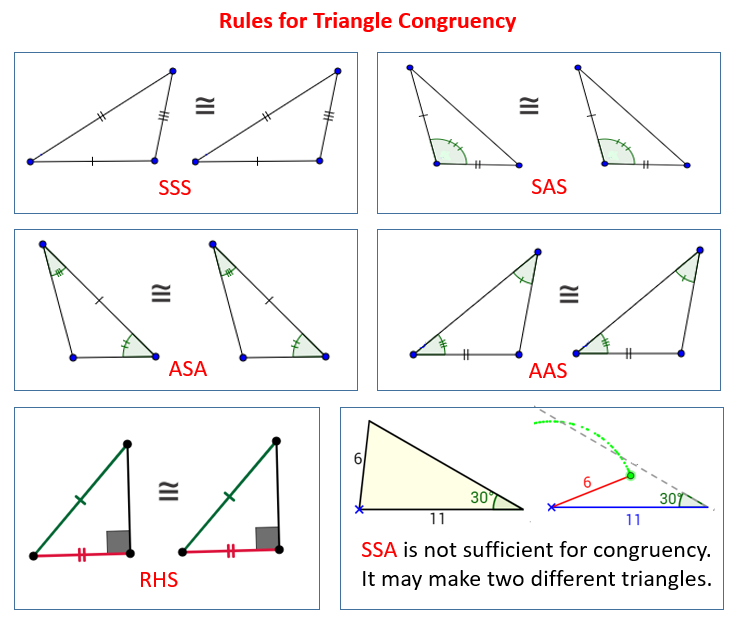
Both SAS and SSS rules are the triangle congruence rules. The full form of SAS is “Side-Angle-Side” and SSS stands for “Side-Side-Side.”
- In the SAS postulate, two sides and the angle between them in a triangle are equal to the corresponding two sides and the angle between them in another triangle.
- In the SSS postulate, all three sides of one triangle are equal to the three corresponding sides of another triangle.
What Does Sss Prove
Why do we use congruent instead of equal?Is congruent to symbol?Are lines equal or congruent?What another word for could?What is a better word for was?What are the similarities and differences of every individual?How do you use similarities in a sentence?What are the similarities between plants and animals?Can you write cow in 13 letters?Why do British say H wrong?What are the 7 letter words?What is the difference between and in math?
Was this information helpful?
Also Check: Ccl4 Electron Geometry
What Is The Difference Between Ssa And Sas
4.9/5differenceSASSSA
Furthermore, how do you tell if a triangle is SAS or SSA?
SAS stands for “side, angle, side” and means that we have two triangles where we know two sides and the included angle are equal. If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.
Also Know, is SSA a congruence shortcut? Four shortcuts allow students to know two triangles must be congruent: SSS, SAS, ASA, and AAS. Knowing only side-side-angle does not work because the unknown side could be located in two different places.
Also Know, what is the difference between AAS and ASA?
While both are the geometry terms used in proofs and they relate to the placement of angles and sides, the difference lies in when to use them. ASA refers to any two angles and the included side, whereas AAS refers to the two corresponding angles and the non-included side.
Is there an SSA congruence?
Same as the Angle Side Side Postulate If two triangles have two congruent sides and a congruent non included angle, then triangles are NOT NECESSARILLY congruent. This is why there is no Side Side Angle and there is no Angle Side Side postulate.
Congruent Meaning In Maths
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is same as the other.
Recommended Reading: Ccl4 Lewis Structure Shape
How Can You Tell If Triangles Are Congruent
You could cut up your textbook with scissors to check two triangles. That is not very helpful, and it ruins your textbook. If you are working with an online textbook, you cannot even do that.
Geometricians prefer more elegant ways to prove congruence. Comparing one triangle with another for congruence, they use three postulates.
What Is Sss And Sas In Geometry
4.2/5
Consequently, what does SSS stand for in geometry?
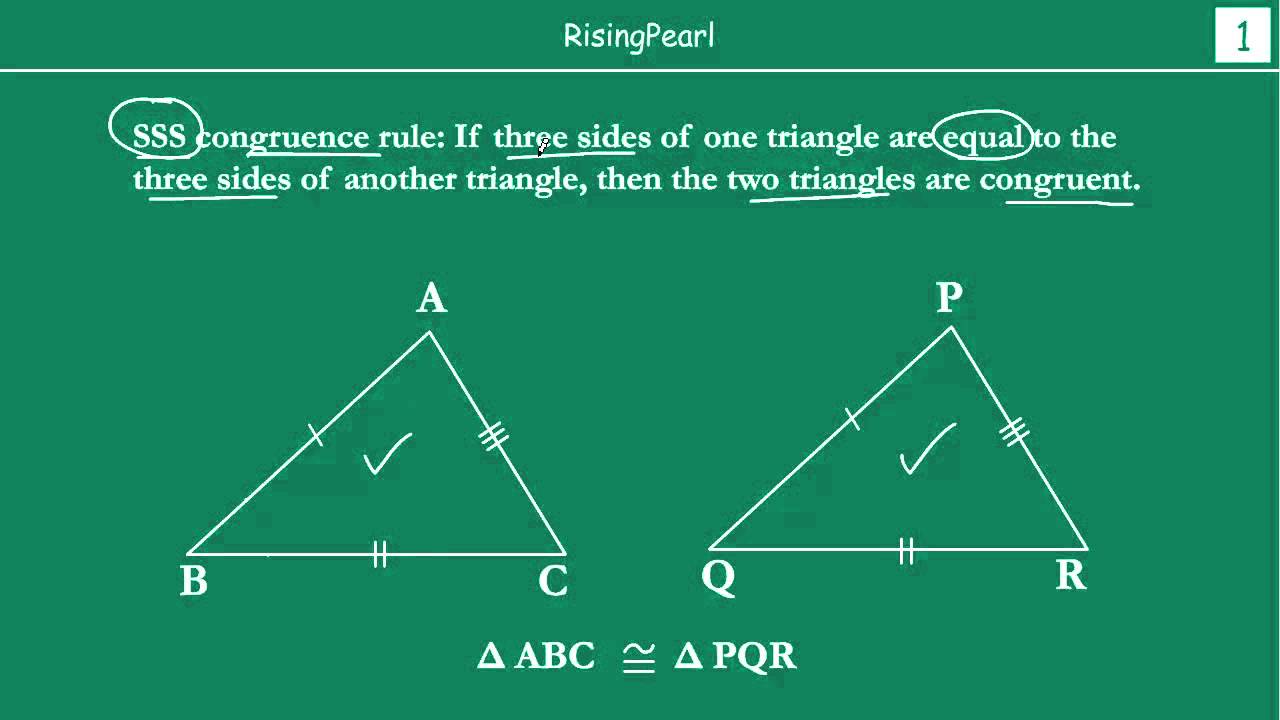
SSS SSS stands for “side, side, side” and means that we have two triangles with all three sides equal. For example: is congruent to: If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.
Likewise, what is SAS rule? Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent. The SAS rule states that. If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.
Additionally, what is SSS SAS ASA AAS?
SSS All three corresponding sides are congruent. SAS Two sides and the angle between them are congruent. ASA
How do you prove the SAS congruence theorem?
SAS Postulate If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.
Don’t Miss: What Is The Molecular Geometry Of Ccl4
Example Question #: Explain How The Criteria For Triangle Congruence Follow From The Definition Of Congruence In Terms Of Rigid Motions
In terms of rigid motion, how do we know when two figures are congruent to one another?
Possible Answers:
Two figures are congruent if there is a sequence of rigid motions that maps one figure to another
Two figures are congruent if there is a sequence of rigid motions that maps at least two vertices to another
Two figures are congruent if they meet the criteria of one of the following theorems: SAS, ASA, SSS
Two figures are congruent if they meet the criteria of all three of the following theorems: SAS, ASA, SSS
Correct answer:
Two figures are congruent if there is a sequence of rigid motions that maps one figure to another
This is the correct definition in terms of rigid motions. Some of the other options are correct definitions for congruence but do not mention the criteria of there being rigid motion between the two figures. An example of this is that and are congruent because they are a reflection of one another. Their vertices that map to each other are
What Do You Mean By Side Angle Side
SAS congruence is the term which is also known as Side Angle Side congruence, which is used to describe the relation of two figures that are congruent. Let’s discuss the SAS congruence of triangles in detail to understand the meaning of SAS. Look at ABC and PQR:
These two triangles are of the same size and shape. Thus, we can say that these are congruent. They can be considered as congruent triangle examples. We can represent this in a mathematical form using the congruent triangles symbol . . This means D falls on P, E falls on Q, and F falls on R. ED falls on PQ, EF falls on QR, and DF falls on PR. Thus, we can conclude that the corresponding parts of the congruent triangles are equal.
Recommended Reading: Why Are There Different Branches Of Chemistry
What Does Sss Stand For
What does SSS mean? This page is about the various possible meanings of the acronym, abbreviation, shorthand or slang term: SSS.
Filter by:
- Selective Service, Selective Service System, SSS
- an independent federal agency that administers compulsory military service
Popularity rank for the SSS initials by frequency of use:
Couldn’t find the full form or full meaning of SSS?
Maybe you were looking for one of these abbreviations:
Discuss these SSS abbreviations with the community:
Report Comment
We’re doing our best to make sure our content is useful, accurate and safe.If by any chance you spot an inappropriate comment while navigating through our website please use this form to let us know, and we’ll take care of it shortly.
The Sas Similarity Rule
The SAS similarity criterion states that If two sides of one triangle are respectively proportional to two corresponding sides of another, and if the included angles are equal, then the two triangles are similar.
Given: DE/AB=DF/AC and D=A. To prove: DEF is similar to ABCThe SAS criterion tells us that ABC ~ DEF. Let us see the justification of this.
Construction:
- Take a point X on AB such that AX = DE.
- Through X, draw segment XY BC, intersecting AC at Y.
Proof:
Since XY II BC, we can note that AXY ~ ABC, and thus: AX/AB = AY/AC….
Now, we will show that AXY and DEF are congruent. It is given that DE/AB=DF/AC….
Since AX=DE and from and , we have: DE/AB = AX/AB = AY/AC = DF/AC. Thus, AY=DF
Now, by the SAS congruency criterion, AXYDEFAXYDEF
While we already have, AXY ~ ABC. This means DEF and ABC are similar. Hence Proved.
You May Like: What Does Abiotic Mean In Biology
Caution Don’t Use Aaa
AAA means we are given all three angles of a triangle, but no sides.
This is not enough information to decide if two triangles are congruent!
Because the triangles can have the same angles but be different sizes:
| is not congruent to: |
Without knowing at least one side, we can’t be sure if two triangles are congruent.
What’s A Congruent In Geometry
congruentcongruentcongruent
Exactly equal in size and shape. Congruent sides or segments have the exact same length. Congruent angles have the exact same measure. For any set of congruent geometric figures, corresponding sides, angles, faces, etc. are congruent.
Similarly, what is SSS SAS ASA AAS? SSS All three corresponding sides are congruent. SAS Two sides and the angle between them are congruent. ASA
Also asked, what does it mean to be congruent?
The adjective congruent fits when two shapes are the same in shape and size. If you lay two congruent triangles on each other, they would match up exactly. Congruent comes from the Latin verb congruere “to come together, correspond with.” Figuratively, the word describes something that is similar in character or type.
What are congruent transformations?
Two objects are congruent if they are the same size and shape. A congruence transformation is a transformation that doesn’t change the size or shape of an object. There are three main types of congruence transformations, and those are reflections , rotations , and translations .
Read Also: Theory Of Everything Geometry Dash 2
Congruent Triangles On A Sphere
As with plane triangles, on a sphere two triangles sharing the same sequence of angle-side-angle are necessarily congruent . This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point thus ASA is valid.
The congruence theorems side-angle-side and side-side-side also hold on a sphere in addition, if two spherical triangles have an identical angle-angle-angle sequence, they are congruent .
The plane-triangle congruence theorem angle-angle-side does not hold for spherical triangles. As in plane geometry, side-side-angle does not imply congruence.
What Is The Difference Between Sss And Sas
4.4/5between
Regarding this, how can you tell the difference between SAS and SSS?
Furthermore, what is SSS ASA SAS RHS? SSS Criterion: Side-Side-Side. SAS Criterion: Side-Angle-Side. ASA Criterion: Angle-Side- Angle. RHS Criterion: Right angle- Hypotenuse-Side.
Thereof, what is the difference between SSS SAS ASA AAS?
The “included angle” in SAS is the angle formed by the two sides of the triangle being used. The “included side” in ASA is the side between the angles being used. The “non-included” side in AAS can be either of the two sides that are not directly between the two angles being used.
How many congruence rules are there?
There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL.
Also Check: What Does Abiotic Mean In Biology
What Is Geometry Drawing
If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles … shapes that can be drawn on a piece of paper. Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres.
Triangle Congruency Lesson & Examples
38 min
- Introduction to triangle congruency lesson
- 00:00:13 What are SAS and SSS Postulates?
- 00:07:20
- Are the triangles congruent by SSS?
- 00:18:12 Write SAS, SSS or Not Congruent
- 00:32:20 Complete the two-column proof
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
You May Like: How Did Geography Discourage Greek Unity
Triangle Congruence Postulates Sss & Sas Explained W/ 13 Examples
// Last Updated:
Did you know that there are five ways you can prove triangle congruency?
Jenn, Founder Calcworkshop®, 15+ Years Experience
Its true!
In todays geometry lesson, were going to tackle two of them, the Side-Side-Side and Side-Angle-Side postulates.
Youll quickly learn how to prove triangles are congruent using these methods.
In addition, youll see how to write the associated two column proof.
Lets jump in!
So we already know, two triangles are congruent if they have the same size and shape. This means that the pair of triangles have the same three sides and the same three angles .
Thankfully we dont need to prove all six corresponding parts are congruent we just need three!
Why?
Because if we can show specific sides and/or angles to be congruent between a pair of triangles, then the remaining sides and angles are also equal.
But there is a warning we must be careful about identifying the accurate side and angle relationships!
As Math is Fun accurately states, there only five different congruence postulates that will work for proving triangles congruent. So we need to learn how to identify congruent corresponding parts correctly and how to use them to prove two triangles congruent.
What Does Cpcte Mean In Geometry
Corresponding Parts of Congruent Triangles are Equal
Corresponding Parts of Congruent Triangles are Equal
Subsequently, question is, what does Cpctc mean in geometry? corresponding parts of congruent triangles are congruent
Keeping this in consideration, what is Cpctc and example?
Corresponding Parts of Congruent Triangles are CongruentIt means that if two trangles are known to be congruent , then all corresponding angles/sides are also congruent. As an example, if 2 triangles are congruent by SSS, then we also know that the angles of 2 triangles are congruent.
What is the definition of congruent triangles?
Congruent Triangles. When two triangles are congruent they will have exactly the same three sides and exactly the same three angles. The equal sides and angles may not be in the same position , but they are there.
Read Also: Why Are There Different Branches Of Chemistry
The Sas Congruence Rule
The Side-Angle-Side theorem of congruency states that, if two sides and the angle formed by these two sides are equal to two sides and the included angle of another triangle, then these triangles are said to be congruent.
Verification:
Let’s perform an activity to show the proof of SAS. Given: AB=PQ, BC=QR, and B=Q. To prove: ABC PQR
Place the triangle ABC over the triangle PQR such that B falls on Q and side AB falls along the side PQ.
- Since AB=PQ, so point A falls on point P.
- Since B=Q, so the side BC will fall along the side QR.
- BC=QR, so point C falls on point R. Thus, BC coincides with QR and AC coincides with PR.
So, ABC will coincide with PQR. Therefore, ABCPQR. This demonstrates SAS criterion of congruence.
What Is The Definition Of Sss In Geometry
Definition
SSS SSS stands for “side, side, side” and means that we have two triangles with all three sides equal. For example: is congruent to: If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.
One may also ask, what does SSS and SAS mean in geometry? If all three pairs of corresponding sides are congruent, the triangles are congruent. This congruence shortcut is known as side-side-side . Another shortcut is side-angle-side , where two pairs of sides and the angle between them are known to be congruent.
Also to know is, what is SSS SAS ASA AAS?
SSS All three corresponding sides are congruent. SAS Two sides and the angle between them are congruent. ASA
What is the full form of SSS?
SSS- Side Side Side.
Read Also: What Does Abiotic Mean In Biology
What Is An Example Of A Congruent Shape
Usually, we reserve congruence for two-dimensional figures, but three-dimensional figures, like our chess pieces, can be congruent , too. Think of all the pawns on a chessboard. They are all congruent . To summarize, congruent figures are identical in size and shape the side lengths and angles are the same.
What Is The Sss Rule Of Congruence
The word “congruent” means equal in every aspect or figure in terms of shape and size.
Congruence is the term used to describe the relation of two figures that are congruent.
Now let’s discuss the congruence of triangles.
Look at \ and \ below.
These two triangles are of the same size and shape.
Thus, we can say that they are congruent.
They can be considered as congruent triangle examples.
We can represent this in a mathematical form using the congruent triangles symbol .
| \ |
This means \ falls on \, \ falls on \ and \ falls on \.
Also, \ falls on \, \ falls on \ and \ falls on \.
This indicates that the corresponding parts of congruent triangles are equal.
Read Also: How Do Noise Cancelling Headphones Work Physics
How To Prove Sss Rule Of Congruence
Let’s perform an activity to show SSS proof.
Draw two right-angled triangles with the hypotenuse of 6 inches and one side of 4 inches each.
Cut these triangles and try to place one triangle over the other such that equal sides are placed over one another.
Do you observe that these two triangles superimpose on each other completely?
This means these two triangles are congruent.
This completes the SSS proof.
Do you want to explore more congruency rules?
Here is a simulation for you to explore these properties of congruent triangles.
Side Side Side Postulate
A postulate is a statement taken to be true without proof. The SSS Postulate tells us,
Congruence of sides is shown with little hatch marks, like this: . For two triangles, sides may be marked with one, two, and three hatch marks.
If ACE has sides identical in measure to the three sides of HUM, then the two triangles are congruent by SSS:
You May Like: Angle Addition Postulate Homework 4