How Do You Find The Measure Of An Acute Angle
Acute angles can be measured with the help of a protractor. To measure an acute angle, place the bottom line of the protractor on the baseline and place the center of the protractor on the vertex where the two angles lines meet. Now, consider the bottom scale of the protractor and measure the angle.
Measurement Of An Acute Angle
Measuring an acute angle is a simple task, for which a protractor must be used. Then, the 90° angle is located and the angles below it will be acute angles, except for the 0° angle, by definition.
See how it is done:
Here an acute angle equal to 60° has been measured, which is the characteristic angle of an equilateral triangle.
Acute And Obtuse Triangles
An acute triangle is a triangle with three acute angles . An obtuse triangle is a triangle with one obtuse angle and two acute angles. Since a triangle’s angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle.
Acute and obtuse triangles are the two different types of oblique triangles triangles that are not right triangles because they have no 90° angle.
| Right |
| _} |
Read Also: Figure Ground Psychology
Triangles With Integer Sides
The only triangle with consecutive integers for an altitude and the sides is acute, having sides and altitude from side 14 equal to 12.
The smallest-perimeter triangle with integer sides in arithmetic progression, and the smallest-perimeter integer-sided triangle with distinct sides, is obtuse: namely the one with sides .
The only triangles with one angle being twice another and having integer sides in arithmetic progression are acute: namely, the triangle and its multiples.
There are no acute integer-sided triangles with area = perimeter, but there are three obtuse ones, having sides , , and .
The smallest integer-sided triangle with three rational medians is acute, with sides .
Heron triangles have integer sides and integer area. The oblique Heron triangle with the smallest perimeter is acute, with sides . The two oblique Heron triangles that share the smallest area are the acute one with sides and the obtuse one with sides , the area of each being 12.
Other Types Of Angles
Apart from the above discussed angles, there are other types of angles known as pair angles. They are called pair angles because they appear in pairs to show a certain property. These are:
- Adjacent angles have the same vertex and arm.
- Complementary angles: Pair angles that add up to 90º.
- Supplementary angles: Pair angles whose sum of angles is equal to 180º.
- Vertically Opposite Angles. Vertically opposite angles are equal.
- Alternate Interior Angles: Alternate interior angles are pair angles formed when a line intersects two parallel lines. Alternate interior angles are always equal to each other.
- Alternate Exterior Angles: Alternate exterior angles are simply vertical angles of the alternate interior angles. Alternate exterior angles are equivalent.
- Corresponding Angles: Corresponding angles are pair angles formed when a line intersects a pair of parallel lines. Corresponding angles are also equal to each other.
We saw a brief overview of the different types of angles. Next, we will see the detailed articles on the most common types of angles .
Recommended Reading: Segment Addition Postulate And Midpoint Worksheet
Why Are Acute Angles Important In Geometry
Have you ever used a protractor? If so, you probably remember that you used it to measure angles. The three basic kinds of angles are right angles,obtuse angles, and acute angles. If a basic geometric shape is made of straight lines , it contains at least one of these three types of angles.
In a square, the four inside corners are the four angles of the square. These angles are all right angles . If you took one of these angles and moved one line closer to the other, narrowing the space between them, the angle would measure less than 90° and would be an acute angle. An angle that is greater than 90° is called an obtuse angle. If you kept widening the angle, it would eventually measure 180° and would look exactly like a straight line.
Understanding the difference between angles is one of the first lessons of geometry, and grasping this basic idea is the starting point for learning more complicated geometric concepts. Acute angles are important in many fields that rely on geometry and the exact measurement of shapes. Just think about how many corners are in your house, and youll realize how crucial angles are to architecture.
Definition Of An Acute Angle:
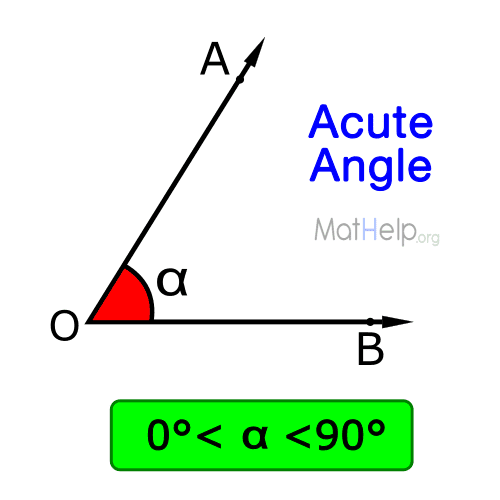
An acute angle is an angle that measures less than 90 degrees.
|
ABC measures 30 and hence it is an acute angle |
A triangle formed by all angles measuring less than 90 is also known as an acute triangle. For example, in an equilateral triangle, all three angles measure 60, making it an acute triangle.
Acute triangle
Dividing the right angle will give us two or more acute angles since each newly formed angle will be less than 90.
-
Right Angle
-
Two acute angles formed by dividing the right angle
Some real-life examples of acute angles are:
If we slice a pizza into 5 or more slices, each slice of pizza will make an acute angle.
Each slice of the pizza makes an acute angle.
Another example is the wall clock. The arms of a wall clock make acute angles at several hours of a day. For example, 2 o Clock.
The hour hand and the minute hand forming an acute angle at 2 o Clock.
|
Fun Facts
|
Read Also: Define Movement In Geography
Positive And Negative Angles
Although the definition of the measurement of an angle does not support the concept of a negative angle, it is frequently useful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions relative to some reference.
In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns. With positive angles representing rotations toward the positive y-axis and negative angles representing rotations toward the negative y-axis. When Cartesian coordinates are represented by standard position, defined by the x-axis rightward and the y-axis upward, positive rotations are anticlockwise and negative rotations are clockwise.
In many contexts, an angle of is effectively equivalent to an angle of “one full turn minus “. For example, an orientation represented as 45° is effectively equivalent to an orientation represented as 360° 45° or 315°. Although the final position is the same, a physical rotation of 45° is not the same as a rotation of 315° .
Acute Angles In Real Life
- The angle made in letter V is an acute angle.
- If we slice a pizza into four or more slices, each slice of pizza will make an acute angle.
- The hands of a wall clock make acute angles at several hours of a day. Example, at 1 oclock.
- The road signs, namely One Way and No Left Turn arrows show an acute angle.
- The turn signal indicator of the dashboard and the speedometer both establish acute angles inside the vehicle.
You May Like: Ccl4 Geometric Shape
What Is Acute Angle
Acute Angle Definition: An angle that is less than 90° is known as an acute angle. The acute angle is otherwise called the angle which is less than the right angle. The acute angle is denoted by the symbol and measured with the help of a protractor in terms of degree.
Acute Angle Examples: Few examples of acute angles in degrees are 80o, 55o, 70o, 25o, 83o, 89o, 15o, 12o, 28o.
A 45o acute angle can be sketched as follows:
Is A Right Angle Triangle An Acute Angle Triangle
No, a right angle triangle is not an acute angle triangle. A right triangle has one of its interior angles to be 90° and the other two angles as 45° each. For a triangle to be an acute angle triangle, all the internal angles need to be less than 90°. So we can say that a right-angled triangle is not an acute triangle.
Don’t Miss: Calculating Half Life
How Many Acute Angles Are In An Acute Triangle
In an acute triangle, all angles are acute. To be an acute triangle, it must have 3 acute angles.
A good example of an acute triangle is an equilateral triangle. The interior angles of all triangles must sum to 180 ° , so in an equilateral triangle, where all three angles have the same measure, we know that each interior angle is an acute 60 angle.
Using Sine Cosine And Tangent To Measure Triangles
If the triangle in question is a right angle, students can use trigonometry in order to find the missing values of the measurements of angles or line segments of the triangle when certain other data points about the figure are known.
The basic trigonometric ratios of sine , cosine , and tangent relate a triangle’s sides to its non-right angles, which are referred to as theta in trigonometry. The angle opposite the right angle is called the hypotenuse and the other two sides that form the right angle are known as the legs.
With these labels for the parts of a triangle in mind, the three trigonometric ratios can be expressed in the following set of formulas:
cos = adjacent/hypotenusesin = opposite/hypotenusetan = opposite/adjacent
If we know the measurements of one of these factors in the above set of formulas, we can use the rest to solve for the missing variables, especially with the use of a graphing calculator which has a built-in function for calculating sine, cosine, and tangents.
Recommended Reading: Who Are Paris Jackson’s Biological Parents
Classification Of Angles On The Basis Of Rotation
Based on the direction of rotation, angles can be classified into two categories, namely
- Positive Angles
- Negative Angles
Positive Angles
Positive angles are the types of angles whose measurements are taken in a counterclockwise direction from the base.
Negative Angles
Negative angles are measured in a clockwise direction from the base.
Alternative Ways Of Measuring The Size Of An Angle
There are several alternatives to measuring the size of an angle by the angle of rotation.The slope or gradient is equal to the tangent of the angle, or sometimes the sine a gradient is often expressed as a percentage. For very small values , the grade of a slope is approximately the measure of the angle in radians.
Inrational geometry the spread between two lines is defined as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines.
Astronomers measure angular separation of objects in degrees from their point of observation.
- 0.5° is approximately the width of the sun or moon.
- 1° is approximately the width of a little finger at arm’s length.
- 10° is approximately the width of a closed fist at arm’s length.
- 20° is approximately the width of a handspan at arm’s length.
These measurements clearly depend on the individual subject, and the above should be treated as rough rule of thumb approximations only.
In astronomy, right ascension and are usually measured in angular units, expressed in terms of time, based on a 24-hour day.
| Unit |
|---|
| 160 minute |
Don’t Miss: Unit 1 Test Geometry Basics Answers Key
Classification Of Angles Based On Their Magnitude
There are seven types of angles based on their degree measurement. They include:
- Zero Angles
A zero angle is an angle formed when both the angles arms are at the same position.
Illustration:
An acute angle is an angle that is more than 0° but less than 90°. Common examples of acute angles include: 15°, 30°, 45°, 60°, etc.
XYZ is greater than 0° but less than 90°
A 90-degree angle, also known as a right angle, is an angle whose measure is equal to 90° is called a right angle. Right angles are represented by drawing a small square box between the arms of an angle.
Illustration:
An obtuse angle is a type of angle whose degree measurement is more than 90° but less than 180°. Examples of obtuse angles are: 100°, 120°, 140°, 160°, 170°, etc.
PQR is an obtuse angle because its less than 180° and greater than 90°.
As the name suggests, a straight angle is an angle whose measure is equal to 180°
Illustration:
Reflex angles are the types of angles whose degree measurement is more than 180° but less than 360°. Common examples of reflex angles are 200°, 220°, 250°, 300°, 350°, etc.
Illustration:
A complete angle is equal to 360°. 1 revolution is equal to 360°.
Illustration:
What Are The Definitions Of A Right Obtuse Or Acute Angle
An angle is the distance, measured in degrees, between two lines that share one endpoint. The exact degree of the angle is measured by a protractor or calculated based on other angles, if using a triangle, which as three sides and three angles total. As an angle increases, the name of the angle changes.
Recommended Reading: Clinical Psychology Subfields
Length Area And Volume
Length, area, and volume describe the size or extent of an object in one dimension, two dimension, and three dimensions respectively.
In Euclidean geometry and analytic geometry, the length of a line segment can often be calculated by the Pythagorean theorem.
Area and volume can be defined as fundamental quantities separate from length, or they can be described and calculated in terms of lengths in a plane or 3-dimensional space. Mathematicians have found many explicit formulas for area and formulas for volume of various geometric objects. In calculus, area and volume can be defined in terms of integrals, such as the Riemann integral or the Lebesgue integral.
Metrics and measures
The concept of length or distance can be generalized, leading to the idea of metrics. For instance, the Euclidean metric measures the distance between points in the Euclidean plane, while the hyperbolic metric measures the distance in the hyperbolic plane. Other important examples of metrics include the Lorentz metric of special relativity and the semi-Riemannian metrics of general relativity.
In a different direction, the concepts of length, area and volume are extended by measure theory, which studies methods of assigning a size or measure to sets, where the measures follow rules similar to those of classical area and volume.
Types Of Angles Explanation & Examples
Different types of angles exist in nature, and each one of them carries much importance in our daily lives.
For example, architects and engineers use angles when designing machines, buildings, roads, and bridges.
In sports, athletes use angles to enhance their performance. For example, a person must spin with the disk at a certain angle to throw it far in short put. In soccer, you must use a certain angle to pass the ball to the next player.
Carpenters and artisans also use angles to fabricate objects such as sofas, tables, chairs, pails, etc. Artists use angles to sketch portraits and paintings. Fashion designers also use angles to come with certain with the best outfits. For these reasons, it is, therefore, necessary we learn the different types of angles.
Don’t Miss: Ct Algebra 1 Curriculum Version 3.0
How To Construct Angles
We use a protractor to construct angles. Lets draw a 50° angle.
- Step 1: First, draw a ray OB and align the protractor with OB as shown.
- Step 2: Place a point above the marking on the protractor that corresponds to 50°.
- Step 3: Remove the protractor and draw a ray beginning at O that passes through this point. Thus, AOB is the required angle, that is AOB = 50°
Note: If the ray extends in the other direction, we measure the angle from the 0° mark on the bottom-left.
The image given below shows how to draw a 50° angle when the ray is pointing in another direction.
Important Notes on Angles
How Do You Find An Acute Angle

To measure an angle, we use a tool called a protractor. When you line up the bottom line of the protractor on one of the angle lines and put the hole that is in the center bottom of the protractor on the corner of the angle, you can find the measure of the angle. Any measure less than 90° is an acute angle.
Recommended Reading: Sacred Geometry Moon Phases Tattoo Spine
Angle Definition In Maths
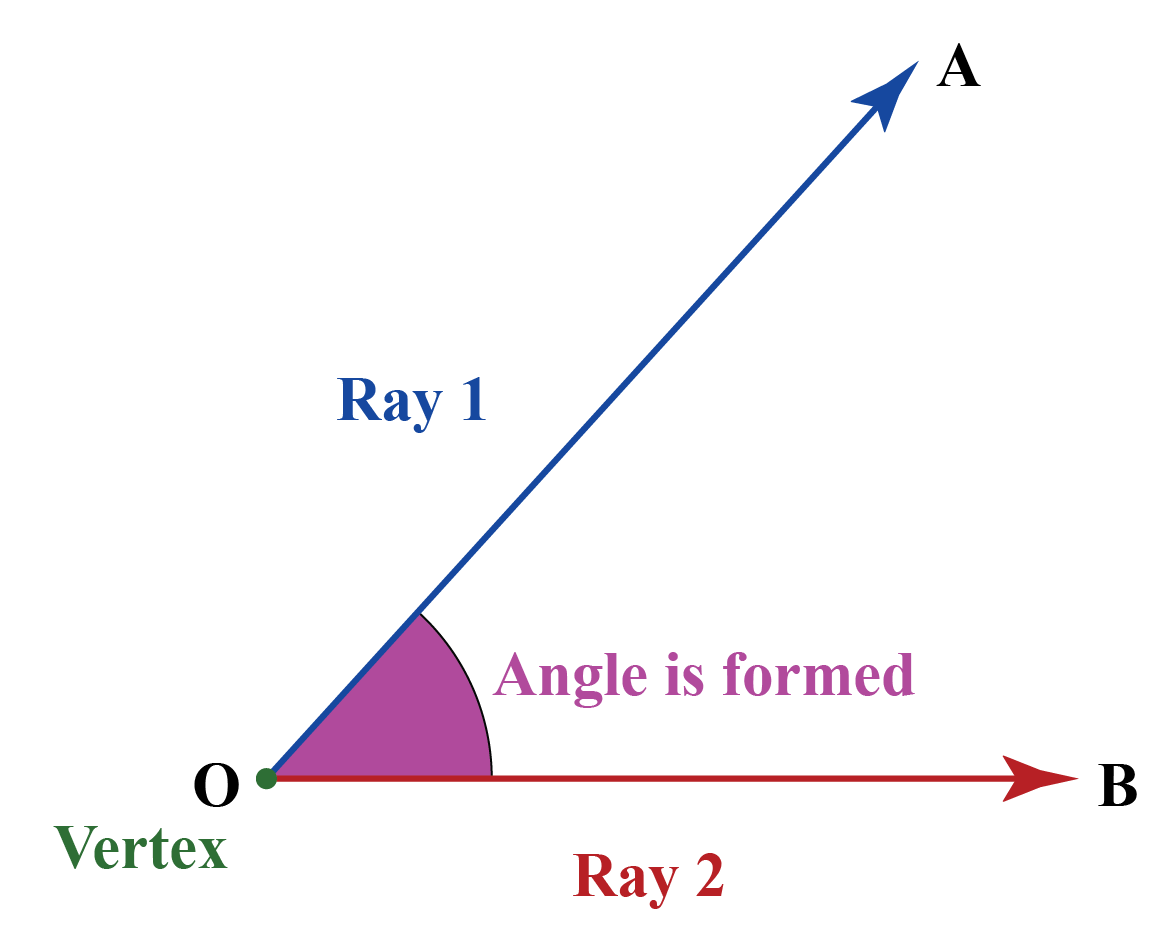
What is an angle? In Plane Geometry, a figure which is formed by two rays or lines that shares a common endpoint is called an angle. The word angle is derived from the Latin word angulus, which means corner. The two rays are called the sides of an angle, and the common endpoint is called the vertex. The angle that lies in the plane does not have to be in the Euclidean space. In case if the angles are formed by the intersection of two planes in the Euclidean or the other space, the angles are considered dihedral angles. The angle is represented using the symbol . The angle measurement between the two rays can be denoted using the Greek letter , , etc. If the angles are measured from a line, we can find two different types of angles, such as a positive angle and a negative angle.
Positive Angle: If the angle goes in counterclockwise, then it is called a positive angle.
Negative Angle: If the angle goes clockwise direction, then it is called a negative angle.
How to Label the Angles?
There are two different ways to label the angles. They are:
Method 1: Give a name to the angle. Generally, the angle is named using the lower case letter like a, x, etc or by using the Greek Letters alpha , beta , theta , etc.
Method 2: By using the three letters on the shapes, we can define the angle. The middle letter should be the vertex .
For example, ABC is a triangle. To represent the angle A is equal to 60 degrees, we can define it as BAC = 60°
How to Measure the Angle?