Find Geometry In Your Name

Progression Of Geometry With Grades

Kindergarten: In kindergarten, children learn to identify and describe two- and three-dimensional shapes. They are able to identify the geometric shapes and names regardless of their orientation. They analyze and compare shapes of different sizes and attributes. They also learn to compose simple shapes to form larger shapes.

Grade 1: In this grade, children develop skills to reason with shapes and the attributes. They understand basic geometric shapes definition. They analyze shapes from their defining attributes, like number of sides. They compose two dimensional and three-dimensional shapes to make larger composite shapes. They learn to partition rectangles and circle into equal shares. They learn the vocabulary related to partitionings like quarters, fourths and halves.

Grade 2: The kids learn to identify and draw shapes according to the given attributes. They learn to draw shapes as per the specified number of faces or geometry angles. They are able to identify cubes, pentagons, hexagons, quadrilateral, and triangles. They also learn to partition a rectangle into same-size squares. They then count these squares to determine the size of the rectangle. The kids learn to partition rectangles and circles into two to four equal shares. They describe the partitioned shapes using the words like half of, third of, thirds, halves. They understand the wholes as four fourths, three-thirds, and two halves.

Lesson 56 Proving Triangle Congruence By Asa And Aas

Monitoring Progress

Question 1.Can the triangles be proven congruent with the information given in the diagram? If so, state the theorem you would use.Answer:

Question 2.In the diagram, \ \, \ \, and \ \ . Prove ABC DEF.Answer:

Question 3.In the diagram, S U and \\ . Prove that RST VYTAnswer:

Geometry Word Problems Involving Perimeter

Example:A triangle has a perimeter of 50. If 2 of its sides are equal and the third side is 5 morethan the equal sides, what is the length of the third side?

Solution:

Let x = length of the equal sides Sketch the figure

Step 2: Write out the formula for perimeter of triangle.

P = sum of the three sides

Step 3: Plug in the values from the question and from the sketch.

50 = x + x + x+ 5

Be careful! The question requires the length of the third side.

The length of third side = 15 + 5 = 20

Answer: The length of third side is 20.

Recommended Reading: Abiotic Science Definition

Adding And Populating A Geometry Column

PostGIS stores a tables spatial information in geometry columns. Usually these columns have the word geom floating around in their name. If you select * on a table with a geometry column, the geom column will look like a long series of nonsense.

Frequently, long/lat values get stored in columns in a database or spreadsheet. To make these into a geometry column that PostGIS understands, we:

Lesson 51 Angles Of Triangles

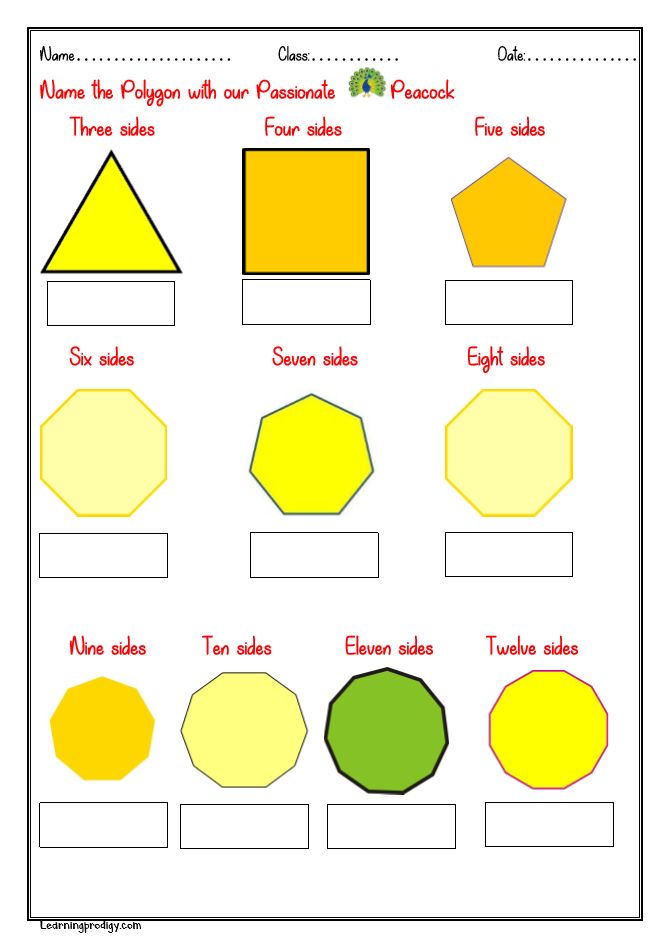
Monitoring Progress

Draw an obtuse isosceles triangle and an acute scalene triangle.Answer:The figures of an obtuse isosceles triangle and an acute triangle are as follows:

Question 2.ABC has vertices A, B, and C, Classify the triangle by its sides. Then determine whether it is a right triangle.Answer:A , B , and C and the triangle is ABCWe know that,To find whether the given triangle is a right-angled triangle or not,We have to prove,AC² = AB² + BC²Where,AC is the distance between A and C pointsAB is the distance between A and B pointsBC is the distance between B and C pointsWe know that,The distance between 2 points = ² + ²Now,Let the given points be considered as A, B, and CSo,AB = ² + ² = 3² + 3²= 9 + 9 = 18BC = ² + ²= ² + 0²AC = ² + ²= ² + 3²

The measure of each acute angle is 90°, 64°, and 26°

Don’t Miss: How Many Physics Questions Are On The Mcat

Make An Angles Display

OK, so its not an activity for the kids exactly, but lets face it: Angles can be pretty tricky when you are trying to learn all the different types and terms. Having a classroom display to help your students remember the different terms and angles is a must! We have a range of posters that are perfect to display in your classroom.

Here are some of our fantastic angle posters available to download today!

How To Uninstall Geometry Dash From Your Pc

If youre not enjoying Geometry Dash, you can find more PC games in the Free Alternative section below.

The easiest way to uninstall Geometry Dash is through the Android emulator. Ill use Bluestacks as an example, but the process is similar for most Android emulators.

Read Also: Who Is Paris Jackson Mother

The 18th And 19th Centuries

Non-Euclidean geometry

It remained to be proved mathematically that the non-Euclidean geometry was just as self-consistent as Euclidean geometry, and this was first accomplished by Beltrami in 1868. With this, non-Euclidean geometry was established on an equal mathematical footing with Euclidean geometry.

While it was now known that different geometric theories were mathematically possible, the question remained, “Which one of these theories is correct for our physical space?” The mathematical work revealed that this question must be answered by physical experimentation, not mathematical reasoning, and uncovered the reason why the experimentation must involve immense distances. With the development of relativity theory in physics, this question became vastly more complicated.

Introduction of mathematical rigor

Analysis situs, or topology

Whos The Ideal Client For Our Geometry Course Completion Service

We serve all sorts of students, but, for the most part, clients fall into one of the categories below:

• Students who want the assurance of a guaranteed high grade in order to protect their GPA and increase their chances of being admitted to the school of their choice, e.g. selective college admissions
• Students who do not want to be bothered with specific projects and assignments that are tedious. Geometry courses in particular are notorious for this
• Students who are currently going through a tough family/personal situation and no longer have the time and energy to devote to their current Geometry course
• Students who simply want to direct their focus to more pressing subjects and interests

Recommended Reading: Hawkes Learning Systems Business Statistics Answers

The Nine Chapters On The Mathematical Art

Areas for the

By the beginning of the 9th century, the “Islamic Golden Age” flourished, the establishment of the House of Wisdom in Baghdad marking a separate tradition of science in the medieval Islamic world, building not only Hellenistic but also on Indian sources.

Although the Islamic mathematicians are most famed for their work on algebra, number theory and number systems, they also made considerable contributions to geometry, trigonometry and mathematical astronomy, and were responsible for the development of algebraic geometry.

Al-Mahani conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. Al-Karaji completely freed algebra from geometrical operations and replaced them with the arithmetical type of operations which are at the core of algebra today.

In some respects, Thabit is critical of the ideas of Plato and Aristotle, particularly regarding motion. It would seem that here his ideas are based on an acceptance of using arguments concerning motion in his geometrical arguments. Another important contribution Thabit made to geometry was his generalization of the Pythagorean theorem, which he extended from special right triangles to all triangles in general, along with a general proof.

Making Points Lines Line Segments And Rays

Finally, students will get creative and use their coloring supplies to make points, lines, line segments, and rays with the letters of their name. Using dots and arrows, students will draw and label at least one point, line, line segment, and ray in their name. Check out the picture below for an example of how this might look:

Here are a few ideas to help you make this geometry activity a success:

• Consider using three separate pieces of graph paper, one for each activity, to prevent too many labels from cluttering up student name pictures.
• You may instead find it helpful to do each geometry activity using a different marker or colored pencil. Use one color for classifying the angles, another color for measuring the angles, and a third color for drawing points, lines, line segments, and rays.
• Give students extra practice by having them do this activity with their first name, middle name, and last name, or using their own name and siblings’ names.

Looking for more fun geometry activities to practice with your elementary-aged students? Check out the interactive geometry lessons on iKnowIt.com today!

Also Check: Prentice Hall Gold Geometry Teaching Resources Answer Key

Geometry And Shapes For Kids: Activities That Captivate

• 57
• 32760

This post contains affiliate links for your shopping convenience. Any purchases made through one of our links earn us a small commission, at no extra cost to you. As an Amazon Associate, I earn from qualifying purchases. All creative ideas and opinions expressed are purely my own. Read our full privacy policy and disclosure for more information.

Learn and build with the geometry and shapes for kids. Tons of fun math activities included and a FREE pattern block symmetry activity!

Were you searching or googling to find engaging, hands-on geometry and shapes for kids? Are you looking for lessons and activity ideas that are fun and build a strong understanding of shapes and geometry? Then you have come to the right place!

Exercise 53 Proving Triangle Congruence By Sas

vocabulary and core concept check

Question 1.What is an included angle?Answer:

Question 2.COMPLETE THE SENTENCEIf two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then __________ .Answer:

Monitoring progress and Modeling with Mathematics

In Exercises 3-8, name the included an1e between the pair of sides given.

Question 3.\ and \Answer:

\ and \Answer:

\ and \Answer:

\ and \Answer:

\ and \Answer:

\ and \Answer:

In Exercises 9-14, decide whether enough information is given to prove that the triangles are congruent using the SAS Congruence Theorem . Explain.

Question 9.

Given \ \, \ \Prove PQT RSTAnswer:

In Exercises 19-22, use the given information to name two triangles that are congruent. Explain your reasoning.

Question 19.SRT URT, and R is the center of the circle.Answer:

ABCD is a square with four congruent sides and four congruent angles.Answer:

RSTUV is a regular pentagon.Answer:

Question 22.\ \, \ \, and M and L are centers of circles.Answer:

CONSTRUCTIONIn Exercises 23 and 24, construct a triangle that is congruent to ABC using the SAS Congruence Theorem .

Question 23.

Describe and correct the error in finding the value of x.Answer:

HOW DO YOU SEE IT?What additional information do you need to prove that ABC DBC?Answer:

Question 27.PROOFThe Navajo rug is made of isosceles triangles. You know B D. Use the SAS Congruence Theorem Answer:

You May Like: Equilateral Geometry Definition

Proving Triangle Congruence By Sas

Exploration 1

Work with a partner.

Use dynamic geometry software.a. Construct circles with radii of 2 units and 3 units centered at the origin. Construct a 40° angle with its vertex at the origin. Label the vertex A.Answer:

b. Locate the point where one ray of the angle intersects the smaller circle and label this point B. Locate the point where the other ray of the angle intersects the larger circle and label this point C. Then draw ABC.Answer:

c. Find BC, mB, and mC.Answer:

d. Repeat parts – several times. redrawing the angle indifferent positions. Keep track of your results by copying and completing the table below. What can you conclude?USING TOOLS STRATEGICALLYTo be proficient in math, you need to use technology to help visualize the results of varying assumptions, explore consequences, and compare predictions with data.Answer:

Communicate Your Answer

Question 2.What can you conclude about two triangles when you know that two pairs of corresponding sides and the corresponding included angles are congruent?Answer:

How would you prove your conclusion in Exploration 1?Answer:

We’ve Done Geometry Work For A Wide Range Of Topics Such As:

• Reasoning and proofs: inductive reasoning, classification, & properties of congruence
• Lines, segments, & rays: Parallel lines, perpendicular lines
• Triangles and congruence: SAS, AAS, SSA, Pythagorean Theorem, Law of Sines, Law of Cosines. Mid-segments, perpendicular bisectors, angle bisectors, medians, & altitudes
• Polygons & Quadrilaterals: parallelograms, rhombi, rectangles, squares, kites, & trapezoids
• Circles: tangent lines, arcs, inscribed angles, chords, secants, & graphs
• Perimeter & area: of triangles, quadrilaterals, polygons, prisms, & circles
• Surface area & volume of polygons, circles, prisms, etc
• Geometric solids : prisms, cylinders, pyramids, cubes, cones, & spheres
• Transformations, congruence, and similarity: rotations, reflections, & dilations, & many more!
• Geometric constructions: constructing bisectors constructing regular polygons inscribed in circles constructing circumcircles and incircles constructing a line tangent to a circle

Don’t Miss: Afda Mean Median Mode Range Practice Answer Key

Congruent Triangles Cumulative Assessment

Question 1.Your friend claims that the Exterior Angle Theorem can be used to prove the Triangle Sum Theorem . Is your friend correct? Explain your reasoning.Answer:

Question 2.Use the steps in the construction to explain how you know that the line through point P is parallel to line m.Answer:

The coordinate plane shows JKL and XYZa. Write a composition of transformations that maps JKL to XYZAnswer:

b. Is the composition a congruence transformation? If so, identify all congruent corresponding parts.Answer:

Question 4.The directed line segment RS is shown. Point Q is located along \ so that the ratio of RQ to QS is 2 to 3. What are the coordinates of point Q? Q

Updating A Geometry Column With Existing Lat/longs

We use two functions to make points out of our latitude/longitude numbers: ST_MakePoint andST_SetSRID.

ST_MakePoint takes the x and y values youre using to make the point. For us, longitude is our x, and latitude is our y. The function requires these numbers to be in the type double precision. If yours arent already you can cast them in the statement as we do below.

St_SetSRID sets the spatial reference system for the point we make. It takes the point and the EPSG code your setting it to. This EPSG code needs to be the same as what you set your geom column to when you added it.

update sandbox.public_bathrooms

• PostgreSQL/PostGIS II: Geometry Types and Coordinate Systems

Don’t Miss: Who Is Paris Jackson Mom

Big Ideas Math Geometry Answers Chapter 5 Congruent Triangles

If you are looking across the web for better preparation resources regarding the Big Ideas Math Geometry Ch 5 Congruent Triangles then this is the one stop destination for all your needs. For better understanding of the concepts we have compiled all the Big Ideas Math Geometry Answers Ch 5 Congruent Triangles in a simple and easy to understand language. Boost your math skills and have a deeper understanding of concepts taking help from the Congruent Triangles BIM Book Geometry Solution Key.

Assigning Numbers To Letters In Your Name

Don’t Miss: Who Is Khloe Kardashian’s Biological Father

Hexagons And Other Shapes

There are all sorts of shapes to be found in flora. Conifers are in the shape of cones , dew drops that coalesce on the leaves of plants are spheres, and salt granules are perfect cubes.

But the most common shape youll find in nature, and the one that most astounds mathematicians, is the hexagon. These six-sided shapes are everywhere! Beehives, insect eyes, and snowflakes are all made up of hexagons. And while free-floating bubbles are often spheres, when a bunch of bubbles mash up against one another, they turn into hexagons!

What shapes can you find around your house or yard?

How To Download Geometry Dash For Android For Free

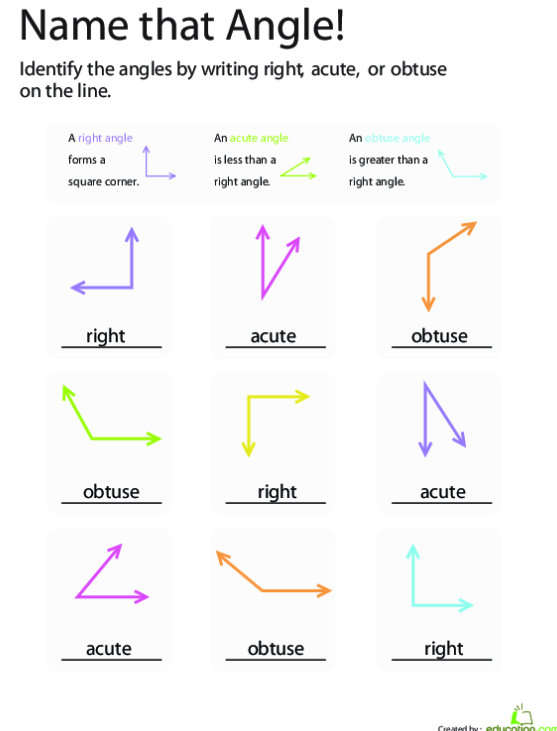
Read Also: Hawkes Learning College Algebra Answers

Lines Rays And Angles

This fourth grade geometry lesson teaches the definitions for a line, ray, angle, acute angle, right angle, and obtuse angle. We also study how the size of the angle is ONLY determined by how much it has “opened” as compared to the whole circle. The lesson contains many varied exercises for students.

When two points are connected with a straight line, we get a line segment. We call this line segment AB or line segmentAB. The sides of a triangleare line segments.

A line has no beginning point or end point. Imagine it continuing indefinitely in both directions.We can illustrate that by little arrows on both ends.

We can name a line using two points on it. This is line EF or line. Or, we can name a line using a lowercase letter: this is line s.

What is an angle? Many people think that an angle is some kind ofslanted line. But in geometry an angle is made up of two rays thathave the same beginning point.

That point is called the vertex and the two rays are called the sidesof the angle.

To name an angle, we use three points, listing the vertex in the middle.This is angle DEF or DEF. We can use the symbol for angle.