Common Core Algebra 1 Unit 2 Equations Formulas Ratio Proportion Chapter Plan
Hi Students, Welcome to Amans Maths Blogs . In this article, you get the full details of Common Core Algebra 1 Unit 2 Equations Formulas Ratio Proportion Chapter Plan. It means, I describe you about Common Core Algebra 1 Unit 2 Equations Formulas Ratio Proportion, what the chapters and lessons plan. Some definitions and important questions with answers and solutions.
Example: What Is 25% Of 160
The percent is 25, the whole is 160, and we want to find the “part”:
Part160 = 25100
Multiply across the known corners, then divide by the third number:
Part = / 100
Answer: 25% of 160 is 40.
Note: we could have also solved this by doing the divide first, like this:
Part = 160 ×
We can also find a Percent:
Ratios And Proportions And How To Solve Them
Let’s talk about ratios and proportions. When we talk about the speed of a car or an airplane we measure it in miles per hour. This is called a rate and is a type of ratio. A ratio is a way to compare two quantities by using division as in miles per hour where we compare miles and hours.
A ratio can be written in three different ways and all are read as “the ratio of x to y”
$$x\: to\: y$$
$$x:y$$
$$\frac$$
A proportion on the other hand is an equation that says that two ratios are equivalent. For instance if one package of cookie mix results in 20 cookies than that would be the same as to say that two packages will result in 40 cookies.
$$\frac=\frac$$
A proportion is read as “x is to y as z is to w”
$$\frac=\frac \: where\: y,w\neq 0$$
If one number in a proportion is unknown you can find that number by solving the proportion.
Example
You know that to make 20 pancakes you have to use 2 eggs. How many eggs are needed to make 100 pancakes?
| 100 |
$$\frac=\frac\: \: or\: \: \frac=\frac$$
If we write the unknown number in the nominator then we can solve this as any other equation
$$\frac=\frac$$
Multiply both sides with 100
$$ }\, \frac= }\, \frac$$
$$x=\frac$$
$$x=10$$
If the unknown number is in the denominator we can use another method that involves the cross product. The cross product is the product of the numerator of one of the ratios and the denominator of the second ratio. The cross products of a proportion is always equal
$$\frac }} }}=\frac }} }}$$
$$xw=yz$$
Don’t Miss: How To Login To Imagine Math
Common Core Algebra 1 Unit 2b Chapter 8 Applications Of Proportions
In this chapter, we will learn about the applications of proportions.
The proportion can be used to solve the questions involving figures, specially similar figure.
A similar figures have exactly the same shape but not necessarily the same shape.
Corresponding sides of two figures are in the same relative position and corresponding angles are equal.
For example: if two triangles ABC and DEF are similar, then
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 8 Question No : 1
In the figure below, if the triangles RST and BCD are similar, then find the value of x.
Common Core Algebra 1 Unit 2 Chapter 8 Solution : 1
Since RST ~ BCD, then RS/BC = RT/BD = ST/CD
RS/BC = RT/BD
8/x = 5/12
x = / 5 = 19.2
Common Core Algebra 1 Unit 2 Chapter 8 Question No : 2
In the figure below, if the hexagons FGHJKL and MNPQRS are similar, then find the value of x.
Common Core Algebra 1 Unit 2 Chapter 8 Solution : 2
Since FGHJKL ~ MNPQRS, then NP/GH = RQ/KJ
6/4 = x/2
x = / 4 = 3
Common Core Algebra 1 Unit 2 Chapter 8 Question No : 3
In the figure below, if the triangles ABC and DEF are similar, then find the value of x.
Common Core Algebra 1 Unit 2 Chapter 8 Solution : 31
Since ABC ~ DEF, then AB/DE = AC/DF = BC/EF
AB/DE = AC/DF
5/4 = 7/x
What Is The Concept Of Ratios

Maths ratio and proportion are used to solve many real-world problems. Register with BYJUS and get solutions for many difficult questions in easy methodology and followed by the step-by-step procedure.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Read Also: Holt Geometry Chapter 7 Test Answer Key
Common Core Algebra 1 Unit 2b Chapter 7 Rates Ratio & Proportion
In this chapter, we will learn about the ratio and proportions.
A ratio is a comparison of two quantities by division. The ratio of a to b can be written a : b or a/b, where b is non-zero. For example: the ration of 1 and 12 is 1 : 12 or 1/12.
Ratios that give same comparison are called as Equivalent ratios. For example: 1/12 and 2/24 are equivalent ratios.
A ratio is differ from fraction. A ratio can be positive or negative but a fraction is always positive.
Read More: 8 Types of Fractions
Now, a statement that two ratios are equivalent is called as Proportion. For example: 1/12 = 2/24 is called Proportion. In proportion, a/b = c/d, the products a.d and b.c are called cross product.
A rate is a ratio of two quantities with different units and second means denominator quantity of 1 unit. For example: 10km/5hour = 2km/1hour. This is the rate.
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 7 Question No : 1
Solve the proportion: 3/z = 1/8.
Common Core Algebra 1 Unit 2 Chapter 7 Solution : 1
Given proportion is 3/z = 1/8.
z x 1 = 3 x 8
z = 24
Common Core Algebra 1 Unit 2 Chapter 7 Question No : 2
Solve the proportion: 9/2 = 5/.
Common Core Algebra 1 Unit 2 Chapter 7 Solution : 2
Given proportion is 9/2 = 5/.
9 x = 2 x 5
9 = 10
= 10/9 1
k = 1/9
Common Core Algebra 1 Unit 2 Chapter 7 Question No : 3
Solve the proportion: 3/ = 4/.
Common Core Algebra 1 Unit 2 Chapter 7 Solution : 3
Given proportion is 3/ = 4/.
3 = 4
3d + 36 3d = 4d + 12 3d
Common Core Algebra 1 Unit 2a Chapter 1 Solving Equations By Adding Or Subtracting
In this chapter, we learn to solve one step equations in one variable by using addition and subtraction.
As we know that an equation is a mathematical statement that two expression are equal and its solution is a value of variable that makes the equation true.
First, note about the properties of equality.
Now, to find the solution of an equation, isolate the variable in one side of the equation by using inverse operation, which undo operation on the variable.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 2 Chapter 1 Question No : 1
Solve x + 7 = 9
Common Core Algebra 1 Unit 2 Chapter 1 Solution : 1
Given equation is x + 7 = 9.
In LHS, we see that 7 is added to the variable x, so to isolate the variable x in LHS, we subtract 7 from the both sides to undo the addition, this is known as inverse operation.
Thus, we get x + 7 7 = 9 7 x = 2. This x = 2 is the solution of the given equation.
Common Core Algebra 1 Unit 2 Chapter 1 Question No : 2
Solve d + 1/2 = 1
Common Core Algebra 1 Unit 2 Chapter 1 Solution : 2
Given equation is d + 1/2 = 1.
In LHS, we see that 1/2 is added to the variable d, so to isolate the variable d in LHS, we subtract 1/2 from the both sides to undo the addition, this is known as inverse operation.
Thus, we get d + 1/2 1/2 = 1 1/2 d = 1/2. This d = 1/2 is the solution of the given equation.
Common Core Algebra 1 Unit 2 Chapter 1 Question No : 3
Solve x 5 = 3
Common Core Algebra 1 Unit 2 Chapter 1 Solution : 3
Also Check: How Do You Find Ksp
Solving Word Problems With Ratios And Proportions Foldable
Want to know something exciting? I taught ratios and proportions in Algebra 1 without once mentioning cross multiplying. Two kids brought it up as an option, but I quickly told them that there was a way to do these problems without cross multiplication. Now, I learned to cross multiply in middle school and did just
Common Core Algebra 1 Unit 2b Chapter 9 Percents
In this chapter, we will learn about the percentage.
A PERCENT is a ratio that compares a number to 100. A percentage is represented as % sign.
To convert a ratio into percent, multiply the ratio with 100 and then write the simplification with % sign.
For example: 1/4 = x 100 = 25%
And, to convert a percentage into a ratio, write the percent with a denominator with of 100, then simplify it.
We can also change it into decimal by dividing the percent by 100, as below.
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 9 Question No : 1
Find 20% of 60.
Common Core Algebra 1 Unit 2 Chapter 9 Solution : 1
Let x represent 20% of 60, then
x = 20% of 60
Thus, 4% of 36 is 1.44.
You May Like: Holt Geometry Workbook Answer Key
Common Core Algebra 1 Unit 2b Chapter 10 Applications Of Percents
In this chapter, we will learn about the applications of percents.
Percents can be used in finding Simple Interest and Sales Tax.
Interest is the amount of money charged for borrowing money, or the amount of money when saving or investing money. Principle is the amount borrowed or invested. Simple Interest is the interest paid only on the principle.
A tip is an amount of money added to a bill for service. It is usually a percent of the bill before sales tax is added. Sales Tax is a percent of an items cost.
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 10 Question No : 1
A telemarketers earns $350 per week plus a 12 % commission on sales. Find her total pay for a week in which her sales are $940.
Common Core Algebra 1 Unit 2 Chapter 10 Solution : 1
Total Pay = Earning Per Week + Commission
Total Pay = 350 +
Total Pay = 350 +
Total Pay = 350 + 42
Total Pay = $392
Common Core Algebra 1 Unit 2 Chapter 10 Question No : 2
Find the simple interest earned after 2 years on an investment of $3000 at 4.5% interest earned annually.
Common Core Algebra 1 Unit 2 Chapter 10 Solution : 2
I = PRT
I = x x
I = x x
I = x x
I = x x
I = $270
Common Core Algebra 1 Unit 2 Chapter 10 Question No : 3
Estimate a 15% tip on a check for $21.98
Common Core Algebra 1 Unit 2 Chapter 10 Solution : 3
First, we round up $21.98 to $22.
Now Tip is about to 15% of $22.
Required tip = 15% of $22
= $2.2 + $1.1 = $3.3
What Is Ratio And Proportion In Maths
The definition of ratio and proportion is described here in this section. Both concepts are an important part of Mathematics. In real life also, you may find a lot of examples such as the rate of speed or price of a material, etc, where the concept of the ratio is highlighted.
Proportion is an equation that defines that the two given ratios are equivalent to each other. For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Let us now learn Maths ratio and proportion concept one by one.
You May Like: 10 Branches Of Chemistry
Common Core Algebra 1 Unit 2a Chapter 6 Solving Absolute Value Equations
In this chapter, we will learn how to solve the equations containing the absolute values.
As we know that an absolute value of a number is the numbers distance from zero on a number line. Absolute of a number x is represented as |x|, which is read as MOD of x.
For example: |5| = 5 and |-5| = 5. It means, for any nonzero value, there are exactly two numbers with that absolute.
Now, we need to ask a question that what the absolute value of x is 5, it means we need to solve for x in the question |x| = 5.
To solve the absolute value equation, perform inverse operations to isolate the absolute value expression on one side of the equation. For this, we need to must consider two cases.
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 6 Question No : 1
Solve for x in the equation |x| = 6.
Common Core Algebra 1 Unit 2 Chapter 6 Solution : 1
Given absolute value equation is |x| = 6.
x = 6 or -6
Common Core Algebra 1 Unit 2 Chapter 6 Question No : 2
Solve for x in the equation |x 3| 6 = 2.
Common Core Algebra 1 Unit 2 Chapter 6 Solution : 2
Given absolute value equation is |x 3| 6 = 2.
|x 3| -6 + 6 = 2 + 6
|x 3| = 8
x 3 = 8 or -8
x 3 + 3 = or
x = 11 or -5
Common Core Algebra 1 Unit 2 Chapter 6 Question No : 3
Solve for x in the equation 3|x| 12 = 18.
Common Core Algebra 1 Unit 2 Chapter 6 Solution : 3
Given absolute value equation is 3|x| 12 = 18.
3|x| 12 + 12 = 18 + 12
3|x| = 30
3|x| / 3 = 30 / 3
|x| = 10
Common Core Algebra 1 Unit 2a Chapter 5 Solving For Variables
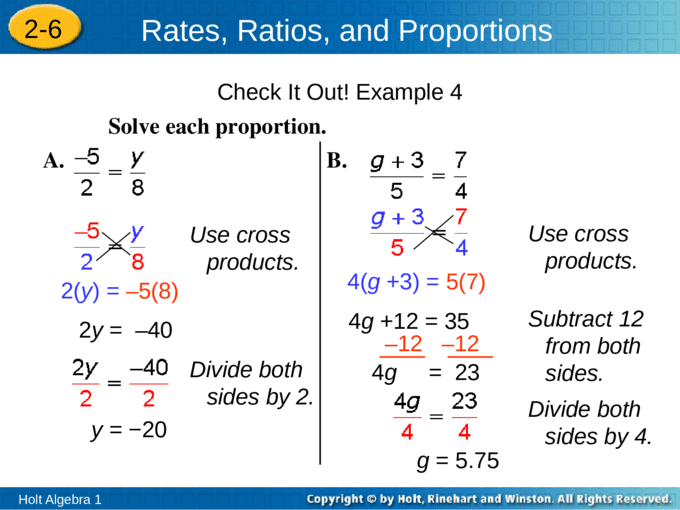
In this chapter, we will learn how to solve the equations for variables in terms of other variables.
A formula is an equation that states a rule for a relationship among quantities. The formula is a type of literal equation with two or more variables
To solve a equation for variable in terms of other variables, we do the following steps.
Step 1: Locate the variables you are asked to solve for in the equation.
Step 2: Identify the operations on this variables and the order in which they are applied.
Step 3: Use inverse operations and isolate the variables.
Lets solve some questions:
Common Core Algebra 1 Unit 2 Chapter 5 Question No : 1
The formula for a Fahrenheit temperature in terms of degree Celsius is F = C + 32. Solve for C.
Common Core Algebra 1 Unit 2 Chapter 5 Solution : 1
Given equation is F = C + 32.
F 32 = C + 32 32
F 32 = C
x = C x
x = C
Thus, C =
Common Core Algebra 1 Unit 2 Chapter 5 Question No : 2
Solve for t in the equation 5 b = 2t.
Common Core Algebra 1 Unit 2 Chapter 5 Solution : 2
Given equation is 5 b = 2t.
/ 2 = 2t / 2
/2 = t
Common Core Algebra 1 Unit 2 Chapter 5 Question No : 3
Solve for n in the equation m/n = p 6.
Common Core Algebra 1 Unit 2 Chapter 5 Solution : 3
Given equation is m/n = p 6.
x n = x n
m = x n
m/ = n
Also Check: Prince Jackson Biological Father
Common Core Algebra 1 Unit 2a Chapter 3 Solving Two Steps & Multi Steps Equation
In this chapter, we learn to solve two or More steps equations in one variable.
To understand better, let an example of equation as
This equation contains multiplication and addition. Equation that contain more than one operation require more than one steps to solve this equation. Identify the order of operations in the equation and order in which they are applied to the variables. Then use inverse operation and work backward to undo them one at a time. Thus, we do the steps as below.
Therefore, we get
3.95c + 19.95 19.95 = 63.40 19.95
3.95c = 43.45
Common Core Algebra 1 Unit 2 Chapter 3 Question No : 3
If 3 = 48, then find x.
Common Core Algebra 1 Unit 2 Chapter 3 Solution : 3
3 = 48
3 / 3 = 48 / 3
x 4 = 16
x 4 + 4 = 16 + 4
x = 20
Common Core Algebra 1 Unit 2a Chapter 4 Solving Equations With Variables On Both Sides
In this chapter, we learn to solve the equations containing variables on both sides.
To understand better, start with an example.
We need to find the value of x in the equation
7k = 4k + 15
To solve such types of equations, first of all we need to collect all variables on one side.
We need to subtract 4k from both sides of the equation
7k 4k = 4k + 15 4k
3k = 15
Since k is multiplied by 3, divided both sides by 3 to undo the multiplication.
k = 5
Common Core Algebra 1 Unit 2 Chapter 4 Question No : 1
If 4b + 2 = -3b, then find b.
Common Core Algebra 1 Unit 2 Chapter 4 Solution : 1
4b + 2 = -3b
4b + 2 + 3b = -3b + 3b
7b + 2 = 0
7b + 2 2 = 0 2
7b = 2
Common Core Algebra 1 Unit 2 Chapter 4 Question No : 2
If 4y + 7 y = 10 + 2y, then find y.
Common Core Algebra 1 Unit 2 Chapter 4 Solution : 2
4y + 7 y = 10 + 2y
3y + 7 = 10 + 2y
3y + 7 2y = 10 + 2y 2y
y + 7 = 10
y + 7 7 = 10 7
y = 3
You May Like: Geometry Segment Addition Postulate Worksheet