Definition Of Bisect In Geometry

Properties Of An Angle Bisector

Angle bisector theorem examples | Geometry | Khan Academy

Till now you must be clear about the meaning of angle bisector in geometry. Now, let us learn some of the angle bisector properties listed below:

An angle bisector divides an angle into two equal parts.
Any point on the bisector of an angle is equidistant from the sides or arms of the angle.
In a triangle, it divides the opposite side into the ratio of the measure of the other two sides.

Construction Of Angle Bisector

Let’s try constructing the angle bisector for an angle. In this section, we will see the steps to be followed for angle bisector construction.

Steps to Construct an Angle Bisector:

Step 1: Draw any angle, say ABC.

Step 2: Taking B as the center and any appropriate radius, draw an arc to intersect the rays BA and BC at, say, E and D respectively.

Step 3: Now, taking D and E as centers and with the same radius as taken in the previous step, draw two arcs to intersect each other at F.

Step 4: Join B to F and extend it as a ray. This ray BF is the required angle bisector of angle ABC.

Definition Of Angle Bisector Example

It will also be helpful to know the definition of a median: a line segment that connects a vertex of a triangle to the midpoint of the side. The bisector of an angle, also called the internal angle bisector , is the line or line segment that divides the. Angle Bisector Theorem. Picture a triangle. Now picture one of the triangles angles being split into two equal smaller triangles. That line. Angle Bisector. An angle bisector is a line or ray that divides an angle into two congruent angles. In the figure, the ray ?KM bisects the angle ?JKL .An angle bisector of a triangle divides the interior angles opposite side into two segments that are proportional to the other two sides of the.

What Is Angle Bisector

The angle bisector in geometry is the ray, line, or segment which divides a given angle into two equal parts. For example, an angle bisector of a 60-degree angle will divide it into two angles of 30 degrees each. In other words, it divides an angle into two smaller congruent angles. Given below is an image of an angle bisector of AOB.

How To Construct An Angle Bisector

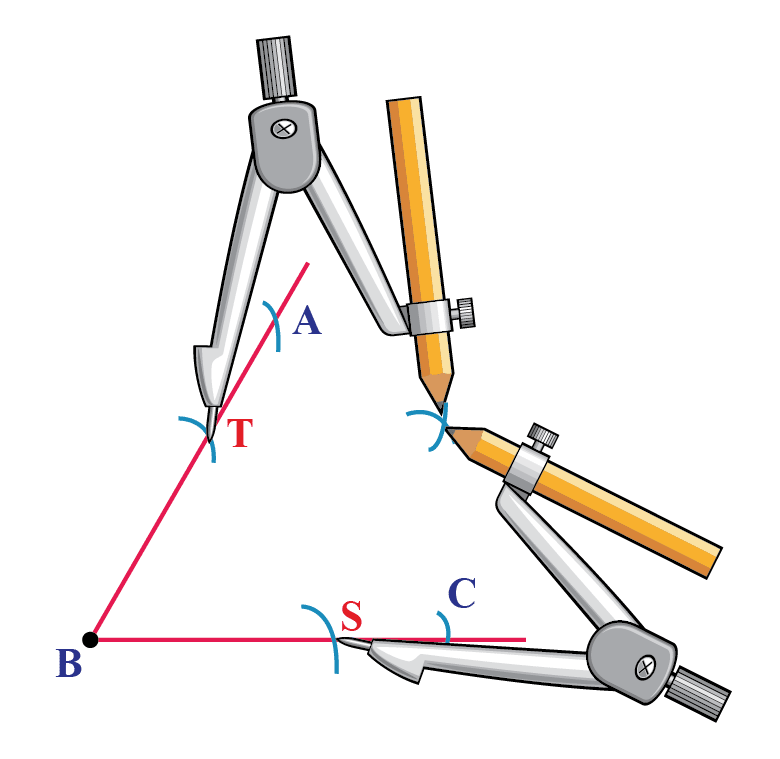
An angle bisector construction can be done by following the steps given below:

Step 1: Take a compass and take any suitable width on it. Place its tip on the vertex of the angle and draw an arc touching the arms of the angle at two distinct points.
Step 2: Keep the same width of the compass and draw arcs intersecting each other from each of those two points.
Step 3: Draw a ray from the vertex of the angle to the point of intersection formed in the previous step.
Step 4: That ray will be the required angle bisector of the given angle.

Don’t Miss: What Is E In Chemistry

How Do You Bisect An Angle Of 60 Degrees

Let’s consider an angle of measure \

Do the following steps to draw a bisector of an angle.

Keeping the sharp end of your compass at \, draw an arc on BC and mark it as \.
Similarly, keeping the sharp end of your compass at \, draw an arc on AB and mark it as \.

Now, keeping the sharp end of your compass at \, draw an arc within \ and \
Repeat the third step at \

Join the point \ and the intersection of the two arcs.
The line is the angle bisector of \.

The line is the angle bisector of \.

How To Bisect A Line Segment

Obviously, one way to bisect a line segment is to measure its length, divide that by two and mark the midpoint. But you can do it without any measurement at all using just a compass and straightedge using techniques developed thousands of years ago by the Greeks.For an animated demonstration of how to do this see Perpendicular bisector of a line segment

Definition Of Angle Bisector In Geometry Proof

One of the most fundamental theorems in mathematics, particularly in geometry, is the Angle Bisector Theorem. According to the Angle Bisector Theorem, The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the. Illustrated definition of Angle Bisector: A line that splits an angle into two equal angles. Try..An angle bisector is a straight line drawn from the vertex of a triangle to its opposite side in such a way, that it divides the angle into two equal or. In geometry, the angle bisector theorem shows that when a straight line bisects one of a triangles angles into two equal parts,

Facts About Segment Bisectors

Angle Bisector – MathHelp.com – Geometry Help

Let’s review and go over some facts about segment bisectors:

A segment bisector, always passes through the midpoint of the segment and divides a segment in two equal parts.
A segment bisector may or may not be a perpendicular bisector.
Points, lines, segments, and rays are all types of segment bisectors. If either a ray or a line serves as a segment bisector, it will be infinite.
A segment may have many bisectors at the same time.

You May Like: Ixl Answer Key Algebra 1

Examples Of Bisect In A Sentence

bisectsbisectedbisect San Diego Union-Tribunebisect Washington Postbisect Outside Onlinebisect Robb Reportbisect The Atlanticbisect Los Angeles Timesbisect WSJbisect Anchorage Daily News

These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘bisect.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

Segment Bisector And Midpoints

In a segment bisector, the point that bisects the lines into two equal halves is called a midpoint. By definition, a midpoint is a point lying in the middle or center of a line joining the two points. For the two points, if a line is drawn joining the two points, then the midpoint is a point at the middle of the line and is equidistant from the two points. Through this midpoint there could be a ray or a line passing by that divides the line into equal parts. Multiply rays or line segments can also pass by the same midpoint as the segment bisector. To determine if the line segment is a segment bisector, we can verify if it crosses on the midpoint and if it does pass on the midpoint, we can use the midpoint formula to find the coordinates of the line. The midpoint formula is:

/2 is average of x-coordinates.
/2 is average of y-coordinates.

You May Like: What Is Pollen Grain In Biology

Bisectors Of The Sides Of A Polygon

Medians

Each of the three medians of a triangle is a line segment going through one vertex and the midpoint of the opposite side, so it bisects that side . The three medians intersect each other at a point which is called the centroid of the triangle, which is its center of mass if it has uniform density thus any line through a triangle’s centroid and one of its vertices bisects the opposite side. The centroid is twice as close to the midpoint of any one side as it is to the opposite vertex.

Perpendicular bisectors

The interior perpendicular bisector of a side of a triangle is the segment, falling entirely on and inside the triangle, of the line that perpendicularly bisects that side. The three perpendicular bisectors of a triangle’s three sides intersect at the circumcenter . Thus any line through a triangle’s circumcenter and perpendicular to a side bisects that side.

In an acute triangle the circumcenter divides the interior perpendicular bisectors of the two shortest sides in equal proportions. In an obtuse triangle the two shortest sides’ perpendicular bisectors are divided by their respective intersecting triangle sides in equal proportions.:Corollaries 5 and 6

For any triangle the interior perpendicular bisectors are given by p

Bisect Definition Math Is Fun

innvoativenaildesign: Definition Of Bisect In Geometry

www.mathsisfun.com
Highest rating: 4
Summary: Illustrated definition of Bisect: To divide into two equal parts. We can bisect line segments, angles, and more. The dividing line is called

See Details

Highest rating: 3
Summary:Bisect means to divide into two equal parts. You can bisect lines, angles, and more. The dividing line is called the bisector

See Details

You May Like: What Is Free Energy In Biology

How Do You Bisect An Angle Of 45 Degrees

Assume you have constructed an angle of measure \

Do the following steps to draw a bisector of this angle.

Keeping the sharp end of your compass at \, draw an arc on BC and mark it as \.
Similarly, keeping the sharp end of your compass at \, draw an arc on AB and mark it as \.

Now, keeping the sharp end of your compass at \, draw an arc within \ and \
Repeat the third step at \

Join the point \ and the intersection of the two arcs.
The line is the angle bisector of \.

What Is Perpendicular Bisector

A perpendicular bisector is a line segment or a ray or a line that intersects a given line segment at a 90o, and also it passes through the midpoint of the line segment. Two lines are said to be perpendicular to each other when they intersect in such a way that they form 90 degrees with each other. A bisector divides a line into two equal halves. Thus, when we talk about the perpendicular bisector of a line segment AB, it implies:

It divides AB into two equal halves or bisects it.
It makes right angles with AB.
Every point in the perpendicular bisector is equidistant from points A and B.

How To Bisect A Line

Do the following steps to draw a bisector of a line.

Draw a line segment \ on a paper.
Taking \ as a center, draw a circle. Just make sure that the radius of the circle should be more than half of the line segment \.
Now, taking \ as a center and with the same radius, draw another circle. Let this circle intersect the previous circle at the points \ and \.
Join the points \ and \.

The line \ is the bisector of the line \.

Definition Of Segment Bisector

Constructing a Perpendicular Bisector – Geometry

Segment bisector is a line, ray, or segment that cuts another line segment at the center dividing the line into two equal halves. The line always bisects or passes through the midpoint of the line segment dividing it into two equal parts. The midpoint can have one or infinite segments bisecting the line and not necessarily be only a perpendicular bisector. Let us look at the image given below.

Line AB is divided into two equal halves i.e. AM and MB by the segment bisector XY. If the line XY cuts the line segment at exactly 90°, it is said to be a perpendicular bisector. But in this case, the line does not cut at a right angle, hence it is a segment bisector. The point M is considered to be the midpoint of the line segment AB where AM = MB.

You May Like: What Does Multiple Mean In Math

Examples Of Bisector In A Sentence

bisectorQuanta Magazinebisector Quanta Magazinebisectors Anchorage Daily Newsbisectors New York Times

These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘bisector.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

How To Construct A Perpendicular Bisector

You will require a ruler and compasses. The steps for the construction of a perpendicular bisector of a line segment are:

Step 1: Draw a line segment PQ.
Step 2: Adjust the compass with a length of a little more than half of the length of PQ.
Step 3: Place the compass pointer at point P and draw arcs above and below the line.

Step 4: Keeping the same length in the compass, place the compass pointer at point Q. Similarly, draw two arcs above and below the line keeping the compass pointer at Q.

Step 5: Mark the points where the opposite arcs cross as X and Y.

Step 6: Using a ruler, draw a line passing across X and Y.

The perpendicular bisector bisects PQ at a point J, that is, the length PJ is equal to JQ. And the angle between the two lines is 90 degrees.

You May Like: How To Do Elimination In Math

Angle Bisector Of A Triangle

In a triangle, the angle bisector of an angle is a straight line that divides the angle into two equal or congruent angles. There can be three angle bisectors in every triangle, one for each vertex. The point where these three angle bisectors meet in a triangle is known as its incenter. The distance between the incenter to all the vertices of a triangle is the same. Look at the image below showing the angle bisector of a triangle. Here, AG, CE, and BD are the angle bisectors of BAC, ACB, and ABC respectively. F is the point of intersection of all three bisectors which is known as incenter and it is at an equal distance from each of the vertex.

Segment Bisectors And Perpendicular Bisectors

Segment bisectors that bisect at 90° are called perpendicular bisectors. A perpendicular bisector is defined as a line or a line segment that divides a given line segment into two parts of equal measurement making four angles of 90° each on both sides. Perpendicular bisector on a line segment can be constructed easily using a ruler and a compass.

Angle Bisector Proportionality Theorem

An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.The Angle-Bisector theorem states that if a ray bisects an angle of a triangle, then it divides the opposite side into segments that are. The Angle Bisector Theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.Angle bisector theorem states that an angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides.

What You’ll Learn:

After working your way through this lesson and video, you will be able to:

Recall and state the definition of a segment bisector
Identify the various forms of segment bisectors, including line segments, lines, rays and points
Recall that a single segment may be bisected by an infinite number of bisectors, only one of which could be a perpendicular bisector

Recommended Reading: What Is The Psychological Approach To The Study Of Law

What You Learned:

Once you view the video, examine the graphics, and read the lesson, you will be able to:

Define the Angle Bisector Theorem
Use ratios and proportion to verify angle bisectors
Identify angle bisectors using the lengths of the sides of triangles
Find the unknown lengths of sides of triangles

Malcolm M.