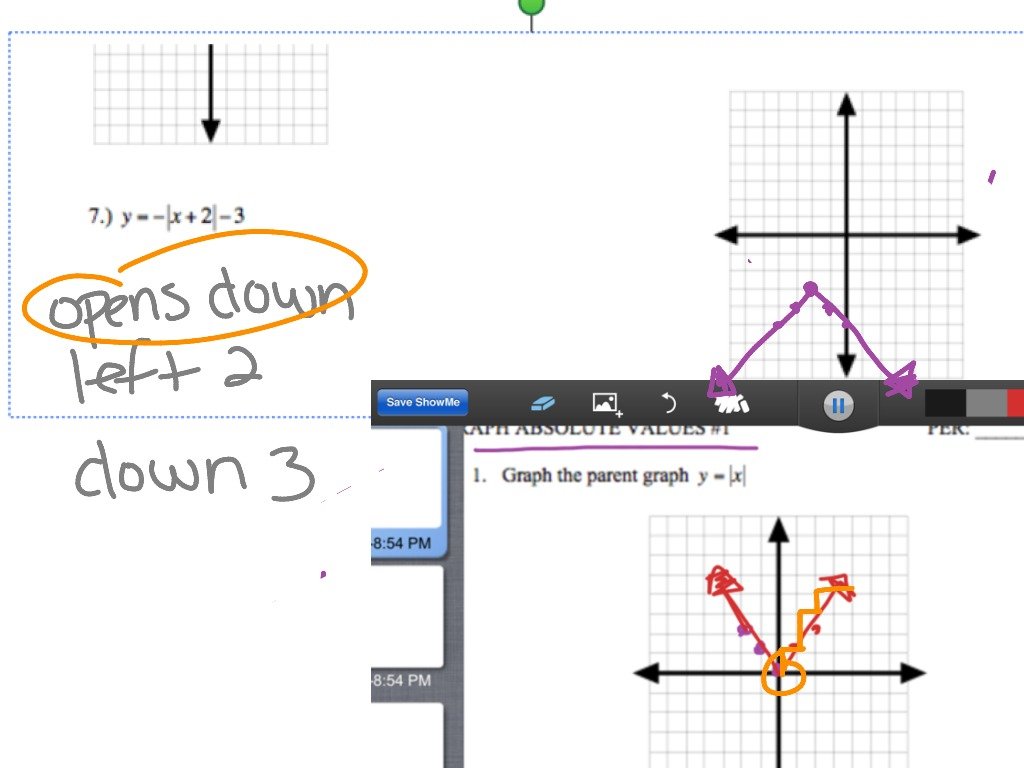
What Is The Definition Of Absolute Value In Math Terms

What Is The Meaning Of Absolute Values

The absolute value of a number is its distance from 0. We know that distance is always a non-negative quantity. Since the absolute value is a distance, the absolute value is always non-negative. Sometimes a sign is attributed to a numeric value to signify the direction, in addition to the value. The increase or a decrease of a quantity, values above or below the mean value, profit, or loss in a transaction, is sometimes explained by assigning a positive or negative value to the numeric value. But for absolute value, the sign of the numeric value is ignored and only the numeric value is considered.

In the above figure, we can observe the absolute values on the number line using the illustration. The absolute value is represented by |x|, and in the above illustration, |4| = |-4| = 4.

What Does Absolute Value Mean

Absolute value describes the distance from zero that a number is on the number line,without considering direction. The absolute value of a number is never negative. Take a look at some examples.

• The absolute value of 5 is 5. The distance from 5 to 0 is 5 units.

• The absolute value of 5 is 5. The distance from 5 to 0 is 5 units.

• The absolute value of 2 + is 5. When representing the sum on a number line, the resulting point is 5 units from zero.

• The absolute value of 0 is 0.

Why Is The Absolute Value Of A Complex Number A Floating Point Number

• 4Mar 9 2018 at 19:15
• How about 5.0 == 5?Mar 9 2018 at 19:16
• 1If the argument of abs is integer the result must be integer, too so it makes sense to have a special integer abs method. But the absolute value of a complex number need not be integer even if the real and the imaginary part are so it makes no sense to have an “integer complex”abs method .

The absolute value of a complex number a+bj, is defined as the distance between the origin and the point in the complex plane. In other words, it’s sqrt.

• Your statement is absolutely correct but does not answer the question. In this particular case, sqrt = 5. Looks like an integer but the function returns a real unlike the abs function that when an integer is input, it returns an integer. It is answered better below.Mar 9 2018 at 23:45

I take it that the real question is Why does Python’s abs return integer values for integer arguments but floating point values for complex numbers with a plain integer value.

Concerning the argument and result types of abs there are three main cases:

• argument is integer result is integer so it’s safe to say that abs returns an integer .
• argument is real result is real so abs returns a floating point number .
• argument is complex the result is a floating point number but the decision whether it has an exact integer value depends on the values of the real/imaginary parts of the argument.

z = 1 + 1jz.real # 1.0z.imag # 1.0

Recommended Reading: Holt Mcdougal Geometry Book Answers

Absolutely Integrable Functions In Signal Processing

Absolutely integrable functions have special importance in signal processing, because absolutely integrable continuous time or discrete time signals are stable and have Fourier transforms. Any signal generated in a lab is going to have these properties. If a signal isnt absolutely integrable, then you cant perform Fourier analysis.

The severe restriction of absolute integrability means that many useful periodic functions like sin t and cos t are not absolutely integrable and do not have Fourier transforms . However, they can be defined on an interval of one time period to enable expression by a Fourier series. An alternative is to analyze the signals or functions with Laplace transform to a complex-valued function).

What Is The Definition Of Absolute Value In Math Terms

Absolute valuenumbernumbernumberabsolute valuenumberabsolute value

. Also, what is absolute value easy?

Absolute value refers to the distance of a number from zero, regardless of direction. The distance is always positive, as absolute value of a number cannot be negative. Use this term to refer to the distance of a point or number from the origin of a number line.

Beside above, what is the absolute value of 8? The absolute value of 8 is 8 .

Beside above, how do you find the absolute value?

The absolute value of a number is the number’s distance from zero, which will always be a positive value. To find the absolute value of a number, drop the negative sign if there is one to make the number positive. For example, negative 4 would become 4.

What do you mean by absolute?

Use absolute as a noun or an adjective when you‘re so sure of something that you know it will never change. Absolute can also mean “without any doubt,” as in the case of an absolute beauty such as a glamorous movie star or a supermodel or “without limits,” such as a dictator who has absolute power over the people.

Recommended Reading: Is Paris Jackson Michael’s Biological Kid

Absolute Value Parent Function

An absolute value function has a unique V shape when plotted on a graph. This is due to the fact that the absolute value of a negative number makes that number positive.

The absolute value parent function.

The absolute value parent function is written as:

f = x where:

• f = x if x > 0
• 0 if x = 0
• -x if x < 0

As the definition has three pieces, this is also a type of piecewise function.Its only true that the absolute value function will hit for this very specific case. Many functions you will come across in calculus will differ in where on the coordinate plane they appear. For example:

Absolutely Integrable Function Defined On An Interval

Many times, youll deal with functions that arent absolutely integrable on their entire domain. However, the condition can be defined in terms of intervals. For example, take some function f, defined on the open interval . If the function is locally integrable and |f| is improperly integrable on the same interval, then the function is absolutely integrable.

The function f = x-2 is absolutely integrable on the interval , has an indefinite integral defined by :.This indefinite integral is continuous and differentiable almost everywhere.

Recommended Reading: How To Figure Out Displacement In Physics

Absolute Value In Number Line

The graph of absolute values is called the absolute value graph. As we know the absolute value of any real number is positive, so the absolute value of any number or function graph will lie on the positive side only.

Example: Graph the absolute value of the number -9.

Solution: Absolute value of |-9| is +9.

So the graph for the absolute value of -9 will look like following

Lesson : Developing The Concept

Materials: Index cards or digital “cards” that can be distributed among the class

Standards:

• Understand the absolute value of a rational number as its distance from 0 on the number line.

Preparation: Make cards for I HaveWho Has?

• Say:Remember that absolute value is the distance that a number is from 0, no matter which direction.
• Ask:Can someone write an equation that means “24 is the absolute value of the number that is 6 less than x?”The equation, 24 = |x 6|, represents the situation. You may need to repeat the equation several times, slowly, as students try to parse it out.
• Ask:What can be the value of the expression inside the absolute value symbols?It is natural to show that x 6 can have a value of 24. Help students see that the expression can also have a value of 24. If necessary, remind them of your previous discussion about directed distance from zero as opposed to absolute distance from zero.
• Ask:If the expression can have a value of 24 or 24, what values can x have?Have students try to find possible values for x themselves at first. Then have them compare what they found, and facilitate a discussion around different strategies they used.If x = 30, then x 6 = 24. If x = 18, then x 6 = 24. There are two possible values for x: 30 and 18.
• Repeat the last three questions using a variety of absolute value expressions:

  |13 x| = 14 |25 + x| = 25 42 = |2x| 1 = |x/36| 0 = |36/x|

Wrap-Up and Assessment Game

Don’t Miss: Blanket Jackson Biological Father

Who Is The Son Of Ra

Ra had two children Shu, the god of air and Tefnut, the goddess of morning dew. They had two children named Nut, the goddess of the sky and Geb, the god of earth. They had four children named Isis, the goddess of home, Nephthys, the goddess of mourning, Set, the god of the desert, and Osiris, god of the afterlife.

What Is The Absolute Value Of A Number

The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.

We can define the absolute values like the following:

|a| =

Note: There is no absolute value for 0 because the absolute value changes the sign of the numbers into positive and zero has no sign.

If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.

You May Like: How To Find Ksp From Molarity

Absolute Value Of A Real Number

If a real number x, the absolute value will satisfy the following conditions.

| x | = x, if x 0

| x | = x, if x < 0

Lets look at the absolute value of 2 in the number line given below. Here, |2| is the distance of 2 from 0. So, both +2 and -2 is the distance of 2 from the origin. But it would be taken as 2 because distance is never measured in negative.

Why Is The Definition Of The Absolute Value $

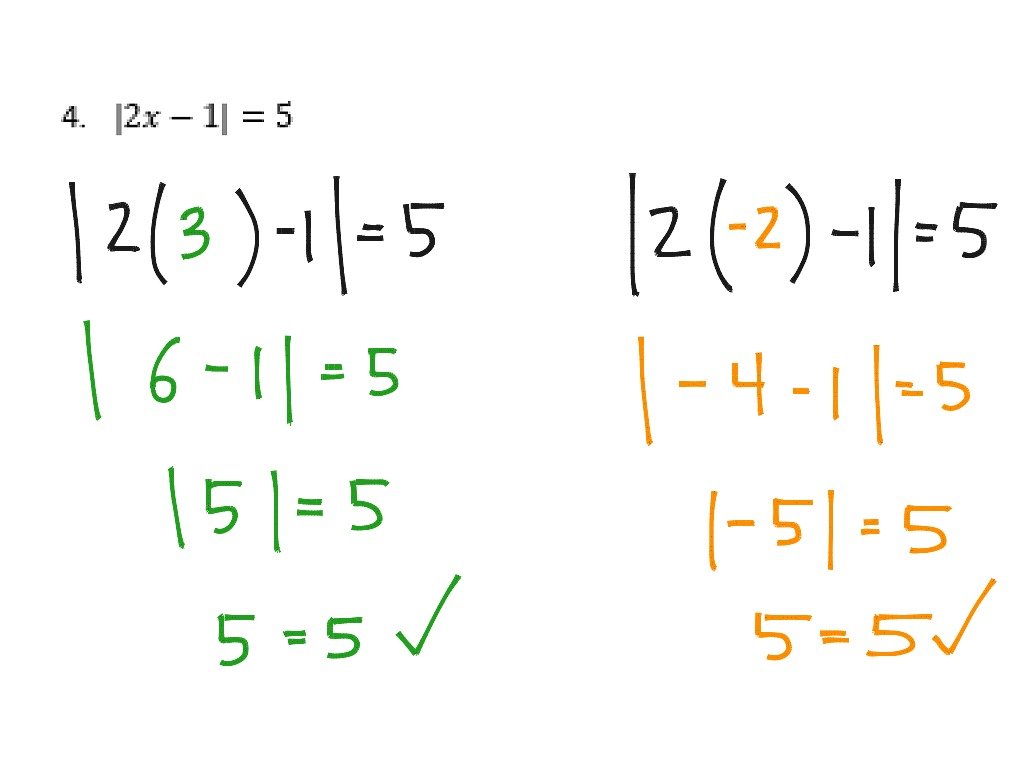
In my notebook it is given that for the above function, we would have:

$f = $

What I don’t get is why did we take $-1$ instead of $0$ as is the case for the function $|x|$? Will the function change substantially if I use $0$ instead of $-1$?

• $\begingroup$You want $|x + 1| \geq 0$. What happens if you use $0$ instead of $-1$?$\endgroup$

$$|x| = \begin x & \mbox x \geq 0 \\ -x & \mbox x < 0. \end$$

The above function says that the function $|x|$ works by adding a minus sign whenever $x$ is negative, making $x$ overall positive and leaving $x$ as it is when $x \geq 0$. Now let’s shift this function to the left by $1$ unit.

We get $$|x+1| = \begin x+1 & \mbox x+1 \geq 0 \\ – & \mbox x+1 < 0. \end$$

But $x+1 \geq 0 \iff x \geq -1$ and similarly for $x+1 < 0 \iff x < -1$ so we can rewrite the above as $$|x+1| = \begin x+1 & \mbox x \geq -1 \\ – & \mbox x < -1. \end$$

This says that whenever $x+1$ is positive, we leave $x+1$ as it is. But $x+1$ is positive as long as $x \geq -1$ However if $x+1$ is negative, then we tack on a minus sign to make it positive again. But $x+1$ is negative whenever $x< -1$.

You can see this from the graph of $|x+1|$ and $x+1$:

You May Like: Algebra 2 Simplifying Radicals With Variables Worksheet

Absolute Value Examples And Equations

The most common way to represent the absolute value of a number or expression is to surround it with the absolute value symbol: two vertical straight lines.

• |6| = 6 means the absolute value of 6 is 6.
• |6| = 6 means the absolute value of 6 is 6.
• |2 x| means the absolute value of the expression 2 minus x.
• |x| means the negative of the absolute value of x.

The number line is not just a way to show distance from zero it’s also a useful way to graph equalities and inequalities that contain expressions with absolute value.

Consider the equation |x| = 2. To show x on the number line, you need to show every number whose absolute value is 2. There are exactly two places where that happens: at 2 and at 2:

Now consider |x| > 2. To show x on the number line, you need to show every number whose absolute value is greater than 2. When you graph this on a number line, use open dots at 2 and 2 to indicate that those numbers are not part of the graph:

In general, you get two sets of values for any inequality |x| > k or |x| k, where k is any number.

Now consider |x| 2. You are looking for numbers whose absolute values are less than or equal to 2. This is true for any number between 0 and 2, including both 0 and 2. It is also true for all of the opposite numbers between 2 and 0. When you graph this on a number line, the closed dots at 2 and 2 indicate that those numbers are included. This is due to the inequality using instead of < .

Why Is The Absolute Value Always Positive

Absolute value means the distance of the number from the origin 0. The number represented on a number line can be negative but the absolute value is always positive since the distance is never negative. For example, the absolute value of -9 is 9 which means that the distance from the number -9 to the origin 0 is 9 units on a number line.

Also Check: Find The Message Pre Algebra With Pizzazz

Definitions And Applications Of Absolute Value

MA, Stanford UniversityTeaching in the San Francisco Bay Area

Alissa is currently a teacher in the San Francisco Bay Area and Brightstorm users love her clear, concise explanations of tough concepts

• Transcript

Sometimes we need to use only positive numbers, and the absolute value is a useful tool for this purpose. When you see an absolute value in a problem or equation, it means that whatever is inside the absolute value is always positive. Absolute values are often used in problems involving distance and are sometimes used with inequalities. Later we will discuss graphs of absolute value equations and inequalities.

Answers By Expert Tutors

In plain English, absolute value is just a certain distance from 0. Since distance is always a positive value , absolute value must also be a positive value.

In your example, -3 is 3 units away from 0, so |-3| is 3. Likewise, multiplying a negative number by a negative number yields a positive product, and -3 * -1 = 3… which happens to be the same distance from 0 that we had gotten before. Thus, |-3| = .

What Jim said was correct. For the person who might not appreciate the absolute value graph, however, perhaps the moonwalking illustration will suffice to get the concept to stick.

Good luck with your studies.

Don’t Miss: Beth Thomas Child Of Rage Now

What Is The Use Of Absolute Value

The absolute value is used to inform the numeric value of a quantity, irrespective of the sign of the quantity. Numerous quantities such as length, price,volume, do not signify any meaning for the sign and are written without any sign. Here the concept of absolute value is helpful to represent such quantities.

What Does It Look Like

The absolute value of 5 is 5, it is the distance from 0, 5 units.

The absolute value of -5 is 5 it is the distance from 0, 5 units.

$$|x| = 2 $$

$$For \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$

|7| = 7 means the absolute value of 7 is 7.

|-7| = 7 means the absolute value of -7 is 7.

|-2 – x| means the absolute value of -2 minus x.

-|x| means the negative of the absolute value of x.

Read Also: Negative Work Physics

What Is The Absolute Value Symbol

To represent the absolute value of a number , we write a vertical bar on either side of the number i.e., |x| where x is an integer. For example, the absolute value of 4 is written as |4|. Also, the absolute value of -4 is written as |-4|. As we discussed earlier, the absolute value results in a non-negative value all the time. Hence, |4|=|-4| =4. That is, it turns negative numbers also into positive numbers. The following figure represents the absolute value symbol.

Important Notes

Are There Any Absolute Monarchies Today

Absolute monarchs remain in the Nation of Brunei, the Abode of Peace the Sultanate of Oman the State of Qatar and the Kingdom of Saudi Arabia. The Kingdom of Bahrain, and the State of Kuwait are classified as mixed, meaning there are representative bodies of some kind, but the monarch retains most of his powers.

Recommended Reading: Why Was The Pail Pale Worksheet Answers

Look Up The Meaning Of Math Words

• Email

• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

This is a glossary of common mathematical terms used in arithmetic, geometry, algebra, and statistics.

Abacus: An early counting tool used for basic arithmetic.

Absolute Value: Always a positive number, absolute value refers to the distance of a number from 0.

Acute Angle: An angle whose measure is between 0° and 90° or with less than 90° radians.

Addend: A number involved in an addition problem numbers being added are called addends.

Algebra: The branch of mathematics that substitutes letters for numbers to solve for unknown values.

Algorithm: A procedure or set of steps used to solve a mathematical computation.

Angle: Two rays sharing the same endpoint .

Angle Bisector: The line dividing an angle into two equal angles.

Area: The two-dimensional space taken up by an object or shape, given in square units.

Array: A set of numbers or objects that follow a specific pattern.

Attribute: A characteristic or feature of an objectsuch as size, shape, color, etc.that allows it to be grouped.

Average: The average is the same as the mean. Add up a series of numbers and divide the sum by the total number of values to find the average.

Base: The bottom of a shape or three-dimensional object, what an object rests on.

Base 10: Number system that assigns place value to numbers.

Capacity: The volume of substance that a container will hold.