Students Who Viewed This Also Studied
Algebra 2 8.03 Writing Assignment-Geometry of Circles.pdf
Keystone National High School
Writing Assignment Geometry of Circles.pdf
Keystone National High School
MATH 10 Angle Pair Relationships Worksheet Solutions
Gladstone Secondary
MATH 10 Exponents and Division Worksheet Solutions
Gladstone Secondary
Keystone National High School MATH Algebra 2
Algebra 2 8.03 Writing Assignment-Geometry of Circles.pdf
homework
Keystone National High School MATH ALGEBRA 2
Writing Assignment Geometry of Circles.pdf
homework
South Paulding High School MATH 123
unit_4a_review_part_2.docx
MATH 10 Angle Pair Relationships Worksheet Solutions
homework
MATH 10 Exponents and Division Worksheet Solutions
homework
Lines And Segments That Intersect Circles
Exploration 1
Lines and Line Segments That Intersect Circles
Work with a partner: The drawing at the right shows five lines or segments that intersect a circle. Use the relationships shown to write a definition for each type of line or segment. Then use the Internet or some other resource to verify your definitions.Chord: _________________Diameter: _________________
Answer:Chord: A chord of a circle is a straight line segment whose endpoints both lie on a circular arc.Secant: A straight line that intersects a circle in two points is called a secant line.Tangent: Tangent line is a line that intersects a curved line at exactly one point.Radius: It is the distance from the centre of the circle to any point on the circle.Diameter: It the straight that joins two points on the circle and passes through the centre of the circle.
Exploration 2
Using String to Draw a Circle
Work with a partner: Use two pencils, a piece of string, and a piece of paper.
a. Tie the two ends of the piece of string loosely around the two pencils.Answer:
b. Anchor one pencil of the paper at the center of the circle. Use the other pencil to draw a circle around the anchor point while using slight pressure to keep the string taut. Do not let the string wind around either pencil.Answer:
What are the definitions of the lines and segments that intersect a circle?Answer:
Question 4.Of the five types of lines and segments in Exploration 1, which one is a subset of another? Explain.Answer:
Inscribed Angles And Polygons
Exploration 1
Inscribed Angles and Central Angles
work with a partner: Use dynamic geometry software.
Sample
a. Construct an inscribed angle in a circle. Then construct the corresponding central angle.Answer:
b. Measure both angles. How is the inscribed angle related to its intercepted arc?Answer:
c. Repeat parts and several times. Record your results in a table. Write a conjecture about how an inscribed angle is related to its intercepted arc.ATTENDING TO PRECISIONTo be proficient in math, you need to communicate precisely with others.Answer:
A Quadrilateral with Inscribed Angles
work with a partner: Use dynamic geometry software.
Sample
a. Construct a quadrilateral with each vertex on a circle.Answer:
b. Measure all four angles. What relationships do you notice?Answer:
c. Repeat parts and several times. Record your results in a table. Then write a conjecture that summarizes the data.Answer:
Communicate Your Answer
Question 3.How are inscribed angles related to their intercepted arcs? How are the angles of an inscribed quadrilateral related to each other?Answer:
Quadrilateral EFGH is inscribed in C. and m E = 80°. What is m G? Explain.
Answer:m E + m H = 80 + 80 = 160°m E + m H + m G + m F = 360160° + m G + m F = 360m G + m F = 360 160 = 200m G = 100°
You May Like: Grade 6 Fsa Warm Ups Answer Key
Lesson 105 Angle Relationships In Circles
Monitoring Progress
Line m is tangent to the circle. Find the indicated measure.
Question 1.
m 6 = 180° = 180° 120°m 6 = 60°
Question 23.PROBLEM SOLVINGYou are flying in a hot air balloon about 1.2 miles above the ground. Find the measure of the arc that represents the part of Earth you can see. The radius of Earth is about 4000 miles.Answer:
Question 24.PROBLEM SOLVINGYou are watching fireworks over San Diego Bay S as you sail away in a boat. The highest point the fireworks reach F is about 0.2 mile above the bay. Your eyes E are about 0.01 mile above the water. At point B you can no longer see the fireworks because of the curvature of Earth. The radius of Earth is about 4000 miles, and \ is tangent to Earth at point T. Find m\. Round your answer to the nearest tenth.Answer:
Question 25.MATHEMATICAL CONNECTIONSIn the diagram, \A is tangent to E. Write an algebraic expression for m\ in terms of x. Then find m\.Answer:
Question 26.MATHEMATICAL CONNECTIONSThe circles in the diagram are concentric. Write an algebraic expression for c in terms of a and b.Answer:
Question 27.ABSTRACT REASONINGIn the diagram. \L is tangent to the circle, and \ is a diameter. What is the range of possible angle measures of LPJ? Explain your reasoning.Answer:
Question 29. are secant lines that intersect at point L. Prove that mJPN > mJLN.Answer:
Answer:Yes, when the circumscribed angle measures 90°, the central angle measures 90°, so the intercepted arc also measures 90°.
Answer:
Circles In The Coordinate Plane
Exploration 1
The Equation of a Circle with Center at the Origin
Work with a partner: Use dynamic geometry software to Construct and determine the equations of circles centered at in the coordinate plane, as described below.a. Complete the first two rows of the table for circles with the given radii. Complete the other rows for circles with radii of your choice.
Answer:
b. Write an equation of a circle with center and radius r.
Answer:x² + y² = r²
Explanation:² + ² = r²x² + y² = r²
Exploration 2
The Equation of a Circle with Center
Work with a partner: Use dynamic geometry software to construct and determine the equations of circles of radius 2 in the coordinate plane, as described below.a. Complete the first two rows of the table for circles with the given centers. Complete the other rows for circles with centers of your choice.
Answer:
b. Write an equation of a circle with center and radius 2.
Answer:² + ² = 4
c. Write an equation of a circle with center and radius r.
Answer:² + ² = r²
Exploration 3
Deriving the Standard Equation of a Circle
Work with a partner. Consider a circle with radius r and center .
Write the Distance Formula to represent the distance d between a point on the circle and the center of the circle. Then square each side of the Distance Formula equation.
How does your result compare with the equation you wrote in part of Exploration 2?
MAKING SENSE OF PROBLEMSTo be proficient in math, you need to explain correspondences between equations and graphs.
Recommended Reading: Who Are Paris Jackson’s Biological Parents
Lesson 107 Circles In The Coordinate Plane
Monitoring Progress
Write the standard equation of the circle with the given center and radius.
Question 1.center: , radius: 2.5
Answer:x² + y² = 6.25
Explanation:² + ² = 2.5²x² + y² = 6.25
Question 2.center: , radius: 7
Answer:² + ² = 49
Explanation:² + ² = 7²² + ² = 49
Question 3.The point is on a circle with center . Write the standard equation of the circle.
Answer:² + ² = 4
Explanation:r = ² + ²= ²² + ² = 2²² + ² = 4
Question 4.The equation of a circle is x2 + y2 8x + 6y + 9 = 0. Find the center and the radius of the circle. Then graph the circle.
Answer:The center of the circle and radius is 4.
Explanation:x² + y² 8x + 6y + 9 = 0x² 8x + 16 + y² + 6y + 9 = 16² + ² = 4²The center of the circle and radius is 4.
Question 5.Prove or disprove that the point lies on the circle centered at the origin and containing the point .
Answer:
Explanation:We consider the circle centred at the origin and containing the point .Therefore, we can conclude that the radius of the circle r = 1, let O and B . So the distance between two points isOB = + ² = = 6As the radius of the given circle is 1 and distance of the point B from its centre is 6. So we can conclude that point does lie on the given circle.
Question 6.why are three seismographs needed to locate an earthquakes epicentre?
Answer:
Circles Maintaining Mathematical Proficiency
z² 2z + 1 = -1 + 1² = 0The solutions are z = 1
Question 13.ABSTRACT REASONINGwrite an expression that represents the product of two consecutive positive odd integers. Explain your reasoning.
Answer:Let us take two consecutive odd integers are x and The product of two consecutive odd integers is x x = x² + 2x
Circles Mathematical Practices
Let A, B, and C consist of points that are 3 units from the centers.
Question 1.Draw C so that it passes through points A and B in the figure at the right. Explain your reasoning.
Answer:
Question 2.Draw A, B, and OC so that each is tangent to the other two. Draw a larger circle, D, that is tangent to each of the other three circles. Is the distance from point D to a point on D less than, greater than, or equal to 6? Explain.
Answer:
Don’t Miss: Is Ap Biology Easy
Lesson 103 Using Chords
In Exercises 1 and 2, use the diagram of D.
Question 1.If m\ = 110°. find m\.
Answer:Because AB and BC are congruent chords in congruent circles, the corresponding minor arcs \, \ are congruent by the congruent corresponding chords theorem.So, \ = \\ = 110°
If m\ = 150° find m\.
Answer:\ = 360 + \)150 = 360 2)2) = 360 150 = 210\ = 105°
In Exercises 3 and 4. find the indicated length or arc measure.
Question 3.
m\ = 9x + 180 x = 180 8xm\ = 180 8x
Question 5.In the diagram, JK = LM = 24, NP = 3x, and NQ = 7x 12. Find the radius of N
Answer:
Vocabulary and Core Concept Check
Question 1.Describe what it means to bisect a chord.Answer:
Question 2.WRITINGTwo chords of a circle are perpendicular and congruent. Does one of them have to be a diameter? Explain your reasoning.
Answer:Imagine a line segment of length 3 units, AB.A second congruent segment of length 3 that is perpendicular to AB called CD.Circumscribe both these line segments and note that AB and CD are now chords.While both chords are perpendicular and congruent, neither chord is a diameter. Thus, it is possible to have two chords of this type with neither one diameter of the circle.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 6, find the measure of the red arc or chord in C.
Question 3.
Use congruent triangles to prove the Perpendicular Chord Bisector Theorem .Given \ is a diameter of L.\ \Prove \ \, \
Answer:
Answer:
Find the missing interior angle measure.
Question 15.
Big Ideas Math Book Geometry Answer Key Chapter 10 Circles
The different chapters included in Big Ideas Math Geometry Solutions are Lines and Segments That Intersect Circles, Finding Arc Measures, Inscribed Angles and Polygons, Angle Relationships in Circles, Segment Relationships in Circles, Circles in the Coordinate Plane, and Using Chords. Students have to practise all the questions from Big Ideas Math Textbook Geometry Chapter 10 Circles.
This Big Ideas Math Book Geometry Answer Key Chapter 10 Circles helps the students while doing the assignments. Get the solutions for all the questions through the quick links provided in the following sections. Test your skills through performance task, chapter review, and maintaining mathematical proficiency.
Don’t Miss: Laws Of Exponents Worksheets 8th Grade
Big Ideas Math Geometry Answers Chapter 10 Circles
Big Ideas Math Book Geometry Chapter 10 Circles Answers are provided here. Students who have been looking for the BIM Geometry Chapter 10 Circles Answers can read the following sections. The high school students can find a direct link to download Big Ideas Math Geometry Answers Chapter 10 Circles pdf for free of cost. With the help of this answer key, you can prepare well for the exam.
Lesson 101 Lines And Segments That Intersect Circles
Monitoring progress
In Example 1, What word best describes \? \?
Answer:\ is secant because it is a line that intersects the circle at two points.\ is the radius as it is the distance from the centre to the point of a circle.
Question 2.In Example 1, name a tangent and a tangent segment.
Answer:\ is the tangent of the circle\ is the tangent segment of the circle.
Tell how many common tangents the circles have and draw them. State whether the tangents are external tangents or internal tangents.
Question 3.
Answer:4 tangents.A tangent is a line segment that intersects the circle at exactly one point. Internal tangents are the lines that intersect the segments joining the centres of two circles. External tangents are the lines that do not cross the segment joining the centres of the circles.Blue lines represent the external tangents and red lines represent the internal tangents.
Question 4.
It is not possible to draw a common tangent for this type of circle.
Question 6.Is \ tangent to C?
Answer:Use the converse of Pythagorean theorem i.e 2² = 3² + 4²4 = 9 + 16By the tangent line to the circle theorem, \ is not a tangent to C
Question 7.\ is tangent to Q.Find the radius of Q.
Answer:The radius of Q is 7 units.
Explanation:By using the Pythagorean theorem² = r² + 24²324 + 36r + r² = r² + 57636r = 576 324
In C, radii \ and \ are perpendicular. are tangent to C.
a. Sketch C, \, \, .
b. What type of quadrilateral is CADB? Explain your reasoning.Answer:
Answer:
Question 7.
Read Also: Calculate Ihd
Exercise 107 Circles In The Coordinate Plane
Vocabulary and Core Concept Check
Question 1.What is the standard equation of a circle?Answer:
Question 2.WRITINGExplain why knowing the location of the center and one point on a circle is enough to graph the circle.
Answer:If we know the location of the center and one point on the circle, we can graph a circle because the distance from the center to the point is called the radius.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 8, write the standard equation of the circle.
Question 3.
x² + y² = 36
Explanation:The center is and the radius is 6² + ² = r²² + ² = 6²x² + y² = 36
Question 5.a circle with center and radius 7Answer:
a circle with center and radius 5
Answer:² + ² = 25
Explanation:² + ² = r²² + ² = 5²² + ² = 25
Question 7.a circle with center and radius 1Answer:
a circle with center and radius 7
Answer:² + ² = 49
Explanation:² + ² = r²² + ² = 7²² + ² = 49
In Exercises 9 11, use the given information to write the standard equation of the circle.
Question 9.The center is , and a point on the circle is .Answer:
The center is , and a point on the circle is .
Answer:x² + y² = 9
Explanation:r = ² + ²= ² + ²
The center is and radius is 6
Explanation:x² + y² + 4y + 4 = 32 + 4x² + ² = 36² + )² = 6²The center is and radius is 6
Question 17.x2 + y2 8x 2y = 16Answer:
x2 + y2 + 4x + 12y = 15
Answer:The center is and radius is 5
Explanation:x2 + y2 + 4x + 12y = 15x² + 4x + 4 + y² + 12y + 36 = -15 + 36 + 4² + ² = 5²The center is and radius is 5
Chapter : Circle Geometry
CHAPTER < strong> 10< /strong> GET READY XX Math Link XX < strong> 10< /strong> .1 Warm Up XX < strong> 10< /strong> .1 Exploring Angles in a < strong> Circle< /strong> XX < strong> 10< /strong> .2 Warm Up XX < strong> 10< /strong> .2 Exploring Chord Properties XX < strong> 10< /strong> .3 Warm Up XX < strong> 10< /strong> .3 Tangents to a < strong> Circle< /strong> XX < strong> Chapter< /strong> Review XX DRAFT Practice Test XX Math Link: Wrap It Up! XX Key Word Builder XX Challenge XX Answers XX
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Angle Relationships In Circles
Exploration 1
Angles Formed by a Chord and Tangent Line
Work with a partner: Use dynamic geometry software.
Sample
a. Construct a chord in a circle. At one of the endpoints of the chord. construct a tangent line to the circle.Answer:
b. Find the measures of the two angles formed by the chord and the tangent line.Answer:
c. Find the measures of the two circular arcs determined by the chord.Answer:
d. Repeat parts several times. Record your results in a table. Then write a conjecture that summarizes the data.Answer:
Angles Formed by Intersecting Chords
Work with a partner: Use dynamic geometry software.
sample
a. Construct two chords that intersect inside a circle.Answer:
b. Find the measure of one of the angles formed by the intersecting chords.Answer:
c. Find the measures of the arcs intercepted h the angle in part and its vertical angle. What do you observe?Answer:
d. Repeat parts several times. Record your results in a table. Then write a conjecture that summarizes the data.CONSTRUCTING VIABLE ARGUMENTSTo be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results.Answer:
Communicate Your Answer
Question 3.When a chord intersects a tangent line or another chord, what relationships exist among the angles and arcs formed?Answer:
Question 4.Line m is tangent to the circle in the figure at the left. Find the measure of 1.Answer:m1 = \ 148m1 = 74°
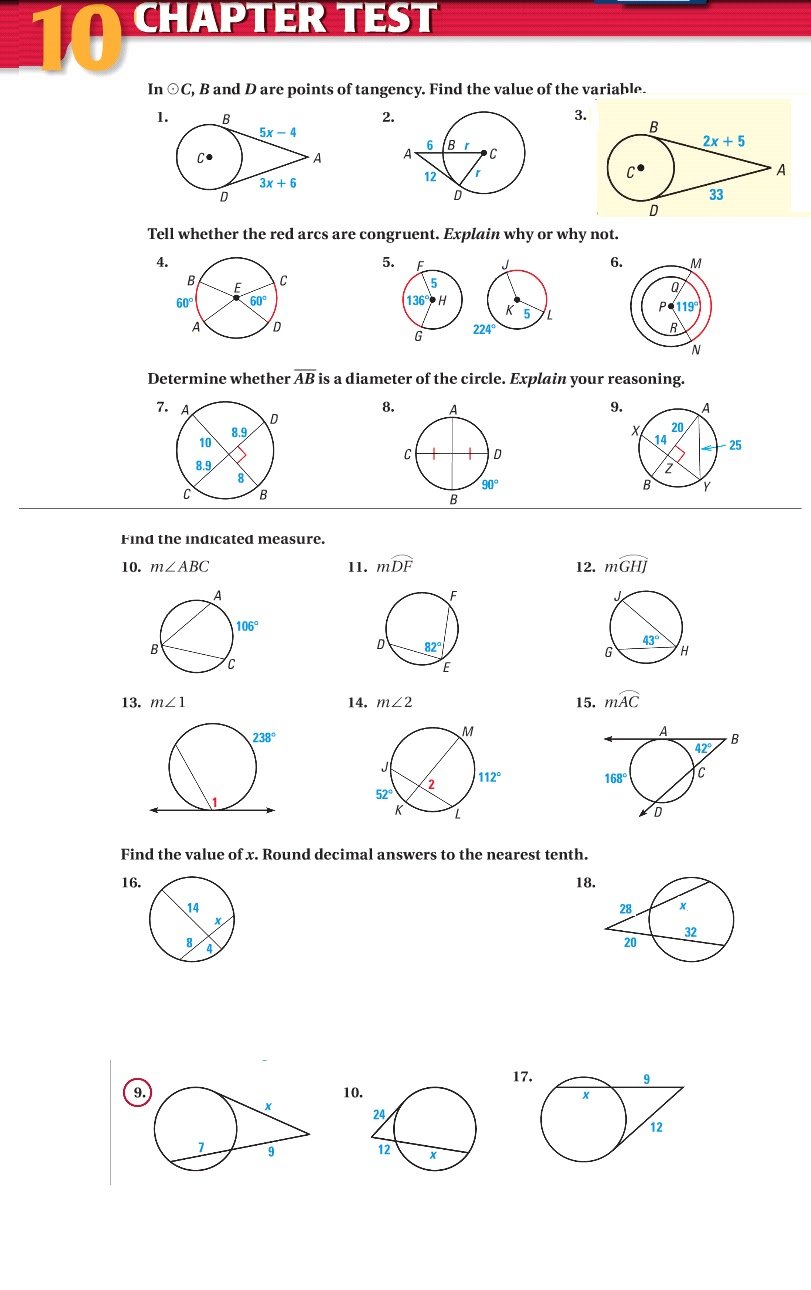
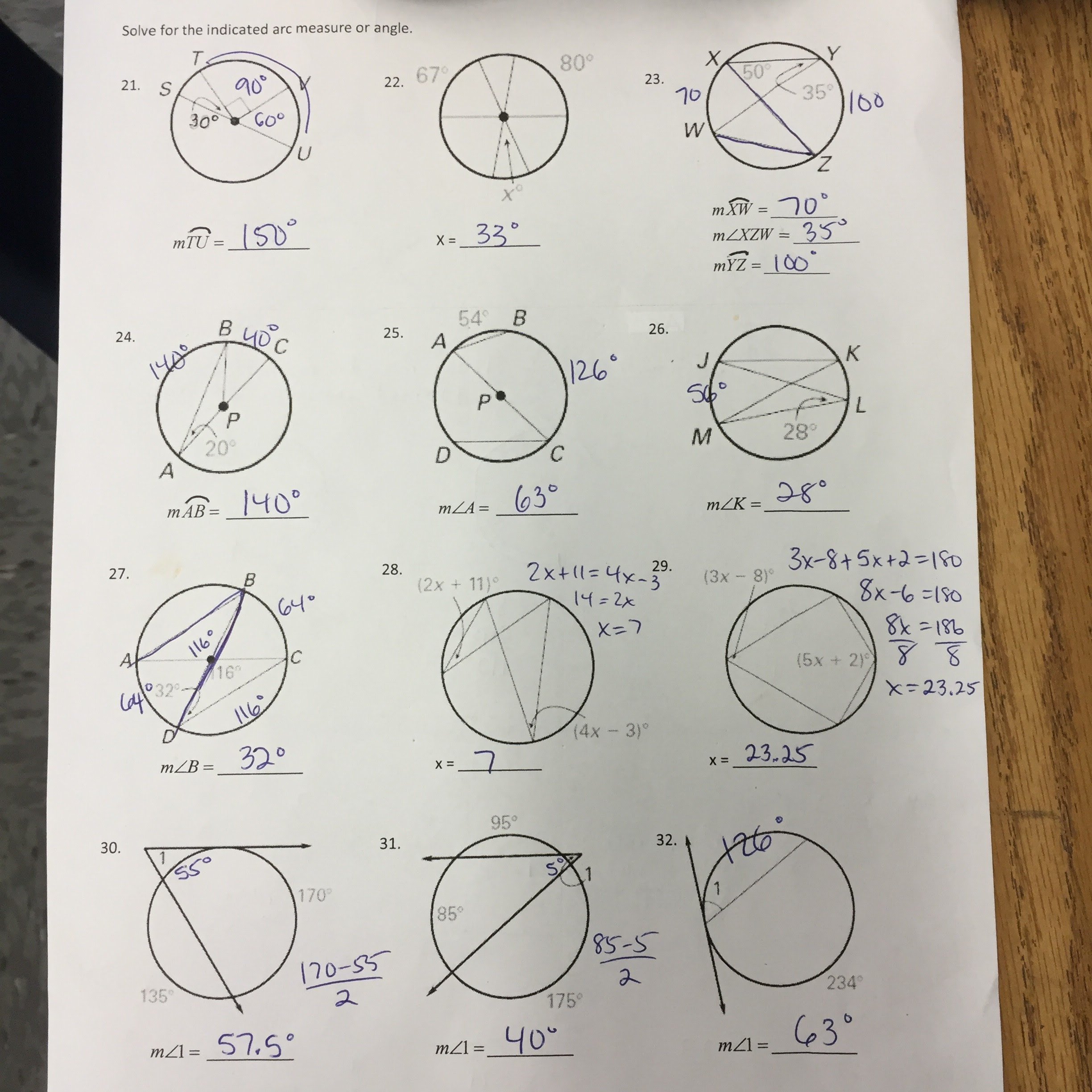
Chapter 10 Circles Geometry Test Answers 40+ Pages Solution In Google Sheet
You can check 28+ pages chapter 10 circles geometry test answers analysis in Google Sheet format. 7 days ago Test your skills with this plane geometry practice exam. Begin with five sheets of plain 81 2 by 11 paper and cut out five large circles that are the same size. Thus the students who feel math is a difficult subject can refer to our Big Ideas Math Answers Grade 8 Chapter 10 Volume and Similar Solids. Check also: circles and chapter 10 circles geometry test answers Whether you are studying for a school exam or just looking to challenge your geometry skills this test will help you assess your knowledge.
Chapter 10 Circles Review DRAFT. Chapter 10 Test A Geometry Answers Chapter 10 Test A Geometry Chapter Test A For use after Chapter 10 The diameter of a circle is given Find the radius 1 d 8 ft 2 d 9 em 3 d 21 m The radius of 08 is given Find the diameter of 0B 4 r 21 em 5 r 33 ft 6 r 29 m Using the diagram below match the notation with the term that best.
On Class 10 Maths The Chapter 10 Resource Mastersincludes the core materials needed for Chapter 10.
Read Also: Introduction To Exponential Functions Common Core Algebra 1 Homework Answer Key