What Is Free Energy In Biology

Free Energy And Biological Processes

In a living cell, chemical reactions are constantly moving towards equilibrium, but never reach it. A living cell is an open system: materials pass in and out, the cell recycles the products of certain chemical reactions into other reactions, and chemical equilibrium is never reached. In this way, living organisms are in a constant energy-requiring, uphill battle against equilibrium and entropy.

When complex molecules, such as starches, are built from simpler molecules, such as sugars, the anabolic process requires energy. Therefore, the chemical reactions involved in anabolic processes are endergonic reactions. On the other hand, the catabolic process of breaking sugar down into simpler molecules releases energy in a series of exergonic reactions. As in the example of rust above, the breakdown of sugar involves spontaneous reactions, but these reactions dont occur instantaneously. An important concept in the study of metabolism and energy is that of chemical equilibrium. Most chemical reactions are reversible. They can proceed in both directions, releasing energy into their environment in one direction, and absorbing it from the environment in the other direction.

Endergonic and Exergonic Processes

Predictive Coding And Free Energy Minimization

Given the form of the generative model , one can now write down the differential describing neuronal dynamics in terms of prediction errors := AT B):

This particular form of generalized filtering is called generalized predictive coding and rests on assuming a Gaussian form for the proposal density in Definition 3: q ) ) . This is known as the Laplace assumption see for an introduction to predictive coding in visual neuroscience and for an introduction to the Laplace assumption in the setting of variational free energy minimization.

This figure provides a schematic overview of the message passing scheme implied by . In this scheme, neurons are divided into prediction and prediction error units that pass messages to each other, within and between hierarchical levels . Superficial pyramidal cells send forward prediction errors to deep pyramidal cells , which reciprocate with predictions that are conveyed by backward connections. This process continues until the amplitude of prediction error has been minimized and the predictions are optimized in a Bayesian sense. The prediction errors are the difference between conditional expectations encoded at any level and top-down or lateral predictions. The Roman numerals designate the cortical layers in which neurons are situated.

Circular Causality And Active Systems

In synergetics and the study of self-organizing systems , one could associate the external states with microscopic system variables that show fast fluctuations, while the internal states might correspond to the macroscopic order parameters that enslave them. The same theme of circular causality is seen in nonlinear Fokker-Planck formulations of coupled nonlinear random dynamical systems , where mean field effects couple back to the density over states by changing their flow. This is a ubiquitous sort of behaviour that arises when some states âseeâ a large number of other states, such that their flow is determined, effectively, by the average over the states they see. This means the microscopic dynamics are caused by macroscopic mean field effects that are constituted microscopic states.

The ergodic density can be characterized by its Shannon entropy, to which the long-term average of self-information or surprisal L) converges, almost surely:

The ergodic density p is an invariant probability measure that can be regarded as the probability of finding the system in any state when observed at a random point in time. The existence of the ergodic density and its underlying attractor ensures the system has invariant characteristics that underwrite its existence over time. Strictly speaking, the entropy in is a differential entropy , because we are dealing with continuous states.

Remarks

H

Proof

Proof

Don’t Miss: Molecular Geometry Of Ccl4

Ergodic Behaviour And Random Dynamical Attractors

To provide some intuition about the sorts of systems that might be modelled in this way, consider two special cases, open and closed systems: open systems have no internal states and X = Sâ Rd. In this case, all states are subject to environmental fluctuations and the flow map corresponds to the solution to stochastic differential equationsâas in . Examples here might include models in computational biology that are used to study self-organizing systems that attain non-equilibrium steady-state or persistence in fluctuating environments . The key aspect of these systems is that they possess a characteristic distribution of physical statesâusually referred to as steady-state and yet operate far from equilibrium. Key examples here range from intracellular kinetics in molecular biology through to neuronal circuits in neuroscience and, at the highest level, the self organisation of entire phenotypes, as studied in theoretical biology and situated cognition.

Standard Energy Change Of Formation

We can say that the standard Gibbs free energy of formation of a compound is basically the change of Gibbs free energy that is followed by the formation of 1 mole of that substance from its component element available at their standard states or the most stable form of the element which is at 25 °C and 100 kPa. Its symbol is fG.

All elements in their standard states have standard Gibbs free energy change of formation equal to zero, as there is no change involved.

fG = fG + RT ln Qf,

where Qf is the reaction quotient.

At equilibrium, fG = 0, and Qf = K, so the equation becomes

fG = RT ln K,

where K is the equilibrium constant.

Read Also: Biotic And Abiotic Meaning

Active Inference And The Free Energy Principle

The notion of random dynamical systems m = that possess internal states allows one to cast self-organization in terms of a deterministic map ÏR:R à X â R , with minimal assumptions about how the system is coupled to the environment through Ïs:R à Ω à X â S, or the dynamics of the environment . In this setting, self-organization can be understood in terms of a circular causality, in which internal states entrain the external states from which they are derived. The outstanding issue is how the deterministic internal map minimizes the surprise or entropy of external states, given that internal states do not âknowâ how they affect external states. Intuitively, the solution considered below regards the system as optimizing a probabilistic model of external dynamics, which is used to minimize surprise. More formally, we want to express the internal states in terms of some real valued and measurable functional F :R ÃXâ R of states that satisfies . To see how this can be done we need to define three further quantities:

Definition 2 : Let the density p|m) defined in be expressed in terms of some arbitrary parameters Ï âΨ that are themselves random variables:

The generative model is then defined by the probability density function p,Ï | m). In statistics p | Ï ,m) is known as the likelihood and p|m) is called a prior. As noted above, p|m) is known as the marginal likelihood or evidence.

Perceptual Precision Attention And Salience

Optimizing the precision parameters corresponds to optimizing the gain of prediction errors . In neuronally plausible implementations of predictive coding, this corresponds to optimizing the excitability of superficial pyramidal cells and has been interpreted in terms of attentional gain.

Concerning the top-down vs bottom-up controversy that has been addressed as a major open problem of attention, a computational model has succeeded in illustrating the circulatory nature of reciprocation between top-down and bottom-up mechanisms. Using an established emergent model of attention, namely, SAIM, the authors suggested a model called PE-SAIM that in contrast to the standard version approaches the selective attention from a top-down stance. The model takes into account the forwarding prediction errors sent to the same level or a level above to minimize the energy function indicating the difference between data and its cause or in other words between the generative model and posterior. To enhance validity, they also incorporated the neural competition between the stimuli in their model. A notable feature of this model is the reformulation of the free energy function only in terms of prediction errors during the task performance:

When gradient descent is applied to action a

You May Like: Si Unit For Distance In Physics

How To Represent Organisms

Free-energy theorists formulate FEP using the traditional modeling tools of random dynamical systems in thermodynamics, and represent organisms adaptive dynamics as trajectories through attractive non-equilibrium states in phase space. For organicists, however, organisms adaptive dynamics cannot be adequately represented with this tool predefined over the characteristic variables individuating kinds of biological systems .

Organicists have different options for justifying this claim. They may deny the existence of an organisms characteristics, or deny that characteristic variables can be reliably identified for any biological system. Another option is to emphasize that the mathematical tools used to represent and explain biological phenomena are merely thatabstract mathematical tools that can be used to describe how one state evolves into another state over time. For instance, Chater and Oaksford forewarn about the risk of conflating scientific models and their targets of the models with this example:

For Longo et al. , organisms should instead be represented as specific, while their trajectories generic. Because of their historicity and materiality, organisms wouldnt possess general characteristics that allow for mathematically invariant representations. They write,

The Second Law Of Thermodynamics

A living cell s primary tasks of obtaining, transforming, and using energy to do work may seem simple enough, but they are more problematic than they appear. The second law of thermodynamics explains why: No energy transfers or transformations in the universe are completely efficient. In every energy transfer, some amount of energy is lost in a form that is unusable. In most cases, this energy is in the form of heat. Thermodynamically, heat energy is defined as the energy transferred from one system to another that is not doing work. For example, when an airplane flies through the air, some of the energy of the flying plane is lost as heat energy due to friction with the surrounding air. This friction heats the air by temporarily increasing the speed of air molecules. Likewise, some energy is lost in the form of heat during cellular metabolic reactions. This is good for warm-blooded creatures like us because heat energy helps to maintain our body temperature. Strictly speaking, no energy transfer is completely efficient because some energy is lost in an unusable form.

Recommended Reading: Which Object Provides An Inertial Frame Of Reference

Gibbs Free Energy And Its Formula

After reading this article you will learn about the gibbs free energy and its formula,which is a process-initiating work obtainable from an isothermal,isobaric thermodynamic system.

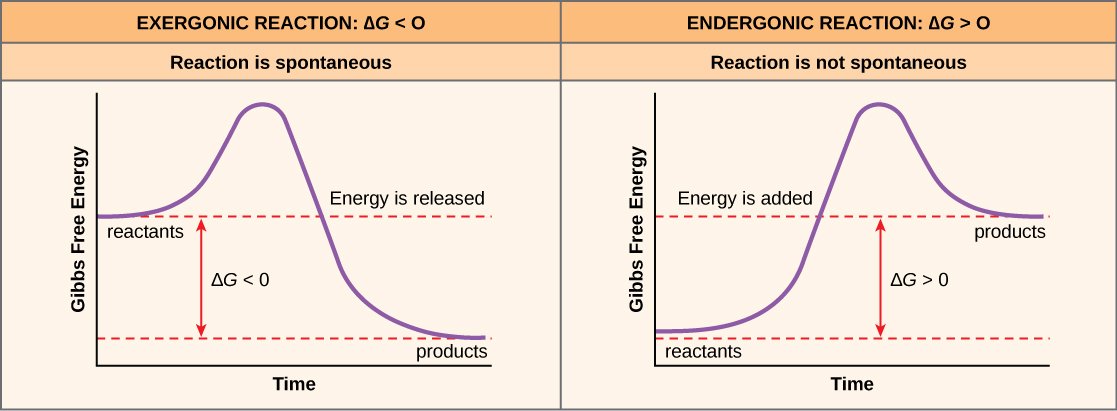
Gibbs free energy is the measures of useful or process-initiating work obtainable from an isothermal, isobaric thermodynamic system. It is the maximum amount of non-expansion work that can be extracted from a closed system this maximum can be attained only in a completely reversible process. When a system changes from a well-defined initial state to a well-defined final state, the Gibbs free energy G equals the work exchanged by the system with its surroundings. The free energy change of a reaction determines its spontaneity. A reaction is spontaneous if G is negative .

For a reaction A + B < -> C + D

Where G= change in free energy, G0 = standard free energy change , R = gas constant, T = absolute temperature

At equilibrium, G equals zero. Solving for G0 yields the relationship at left.

Keq, the ratio / at equilibrium, is called the equilibrium constant.

The standard free energy change of a reaction may be positive and the actual free energy change negative, depending on cellular concentrations of reactants and products. Many reactions for which G0 is positive are spontaneous because other reactions cause depletion of products or maintenance of high substrate concentrations.

Examples of different types of coupling:

Type 1:

ATP + H2O < > ADP + Pi

G° = = -17 kJoules/mol

Type 2:

Free And Activation Energy

After learning that chemical reactions release energy when energy-storing bonds are broken, an important next question is the following: How is the energy associated with these chemical reactions quantified and expressed? How can the energy released from one reaction be compared to that of another reaction? A measurement of free energy is used to quantify these energy transfers. Recall that according to the second law of thermodynamics, all energy transfers involve the loss of some amount of energy in an unusable form such as heat. Free energy specifically refers to the energy associated with a chemical reaction that is available after the losses are accounted for. In other words, free energy is usable energy, or energy that is available to do work.

If a chemical reaction absorbs energy rather than releases energy on balance, then the G for that reaction will be a positive value. In this case, the products have more free energy than the reactants. Thus, the products of these reactions can be thought of as energy-storing molecules. These chemical reactions are called endergonic reactions and they are non-spontaneous. An endergonic reaction will not take place on its own without the addition of free energy.

Also Check: Who Is Paris Jackson Parents

Potential And Kinetic Energy

When an object is in motion, there is energy associated with that object. Think of a wrecking ball. Even a slow-moving wrecking ball can do a great deal of damage to other objects. Energy associated with objects in motion is called kinetic energy . A speeding bullet, a walking person, and the rapid movement of molecules in the air all have kinetic energy.

Figure 4. Still water has potential energy moving water, such as in a waterfall or a rapidly flowing river, has kinetic energy.

Now what if that same motionless wrecking ball is lifted two stories above ground with a crane? If the suspended wrecking ball is unmoving, is there energy associated with it? The answer is yes. The energy that was required to lift the wrecking ball did not disappear, but is now stored in the wrecking ball by virtue of its position and the force of gravity acting on it. This type of energy is called potential energy . If the ball were to fall, the potential energy would be transformed into kinetic energy until all of the potential energy was exhausted when the ball rested on the ground. Wrecking balls also swing like a pendulum through the swing, there is a constant change of potential energy to kinetic energy . Other examples of potential energy include the energy of water held behind a dam or a person about to skydive out of an airplane.

Gibbs Free Energy Problems

Predict whether the following reaction is still spontaneous at 500 °C: N2 + 3 H2 2 NH3. Assume that H = 92.22 kJ mol-1 and S = -198.75 J K-1 mol-1

Solution:

Before we can decide whether the reaction is still spontaneous we need to calculate the temperature of the Kelvin scale:

T = 500° C + 273 = 773 K

We then multiply the entropy term by this temperature and subtract this quantity from the enthalpy term:

G° = H°- TS°

=92,220 J

= 92,220 J

= 61,380 J

G°= 61.4 kJ,

Thus, the reaction is not spontaneous at 773 K because the entropy term becomes larger as the temperature increases, the reaction changes from the one which is favourable at low temperatures to one that is unfavourable at high temperatures.

Suppose that a reaction has H = -28 kJ and S= -60 J/K. At what temperature will it change from spontaneous to non-spontaneous?

Possible Answers:

Solution:

Approximately 467 K. G=H-TS and a reaction proceeds spontaneously when G < 0

and is non-spontaneous when G > 0. So if we set G=0 and solve the equation for T, we will see that the crossover from spontaneous to non-spontaneous occurs when T=467K.

If the reaction quotient is greater than the equilibrium constant , what is true about the Gibbs free energy?

Possible Answers:

Solution:

Predict the following reaction is spontaneous or not at 25°C?

N2 + 3 H2 2 NH3(g

H = -92.22 kJ

Read Also: Geometry Dash Practice Mode

How To Explain Life Phenomena

Free-energy theorists appeal to FEP in explanations of various phenomena, including Hebbs rule and spike-timing dependent plasticity, the multiplicity and hierarchical organization of cortical layers, their reciprocal connection with distinct feedforward and feedback properties, and the existence of adaptation and repetition suppression . Such explanations are thought of axiomatically, as logical deductions from sets of axioms and formulae . Stipulative definitions, like living system as an attracting set in a phase space or adaptive behavior as behavior that reduces average surprise, provide the bridge principles that connect theoretical predicates from different disciplines, and that allow free-energy theorists to attempt the deductions needed to claim reductions of other principles to FEP. In their sweeping attempt to explain these and other phenomena, and to reduce their theories and principles to FEP, free-energy theorists have also claimed for their theory another virtue: a grand theoretical unification .

In presenting these features, FEP is apparently at odds with mechanists emphasis that life science phenomena should be explained by appeal to mechanisms, and that adequate strategies for explanation in the life sciences should involve decomposing these mechanisms into component parts and operations and providing an account of how these parts and operations work together to produce the phenomenon.

Relationship Between Free Energy And Equilibrium Constant

The free energy change of the reaction in any state, G is related to the standard free energy change of the reaction, G° according to the equation.

G = G° + RT InQ

Where Q is the reaction quotient.

At equilibrium,

G=0 and Q become equal to the equilibrium constant. Hence the equation becomes,

G° = RT In K

G° = 2.303 RT log K

R = 8.314 J mol-1 K-1 or 0.008314 kJ mol-1 K-1.

T is the temperature on the Kelvin scale

In a reversible reaction, the free energy of the reaction mixture is lower than the free energy of reactants as well as products. Hence, free energy decreases whether we start from reactants or products i.e, G is -ve in backward as well as forward reactions.

Don’t Miss: What Does Abiotic Mean In Biology