What Are Equal Sets
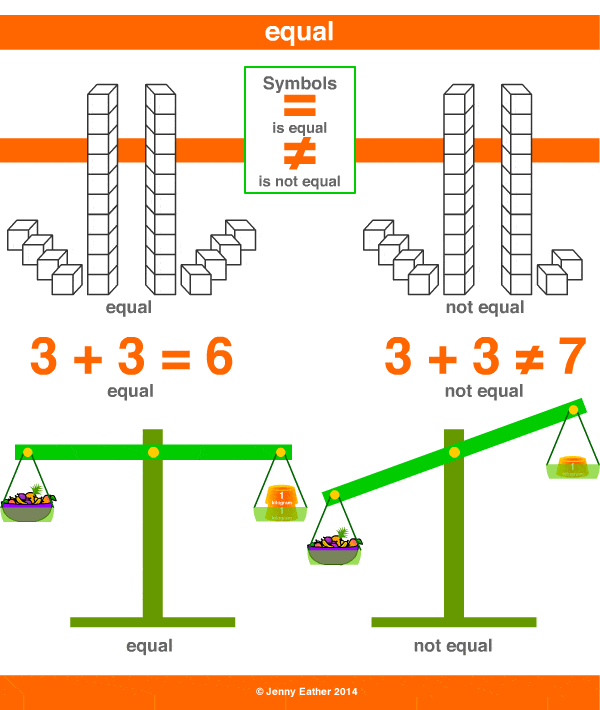
Equal sets are defined as the sets that have the same cardinality and all equal elements. In other words, two or more sets are said to be equal sets if they have the same elements and the same number of elements. For example set A = and B = . Then sets A and B are said to be equal sets as their elements are the same and they have the same cardinality.
Now, two sets are said to be unequal sets if all the elements are not the same in two sets, and sets that have the same number of elements are called equivalent sets. For example, if A = , C = , and D = . Sets A and C have the same number of elements but all the elements are not equal. Therefore, A and C are equivalent sets. Now, sets A and D do not have the same cardinality and the elements are also not equal. Therefore, sets A and D are unequal sets. The equal and equivalent sets can be understood from the number of elements and the similarity of elements of the two sets.
An Intuitive Guide To Exponential Functions & E
e has always bothered me not the letter, but the mathematical constant. What does it really mean?
Math books and even my beloved Wikipedia describe e using obtuse jargon:
The mathematical constant e is the base of the natural logarithm.
And when you look up the natural logarithm you get:
The natural logarithm, formerly known as the hyperbolic logarithm, is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718281828459.
Nice circular reference there. Its like a dictionary that defines labyrinthine with Byzantine: its correct but not helpful. Whats wrong with everyday words like complicated?
Im not picking on Wikipedia many math explanations are dry and formal in their quest for rigor. But this doesnt help beginners trying to get a handle on a subject .
No more! Today Im sharing my intuitive, high-level insights about what e is and why it rocks. Save your rigorous math book for another time. Heres a quick video overview of the insights:
What About Different Rates
Good question. What if we grow at 50% annually, instead of 100%? Can we still use e?
Lets see. The rate of 50% compound growth would look like this:
Hrm. What can we do here? Remember, 50% is the total return, and n is the number of periods to split the growth into for compounding. If we pick n=50, we can split our growth into 50 chunks of 1% interest:
Sure, its not infinity, but its pretty granular. Now imagine we also divided our regular rate of 100% into chunks of 1%:
Ah, something is emerging here. In our regular case, we have 100 cumulative changes of 1% each. In the 50% scenario, we have 50 cumulative changes of 1% each.
What is the difference between the two numbers? Well, its just half the number of changes:
This is pretty interesting. 50 / 100 = .5, which is the exponent we raise e to. This works in general: if we had a 300% growth rate, we could break it into 300 chunks of 1% growth. This would be triple the normal amount for a net rate of $e^3$.
Even though growth can look like addition , we need to remember that its really a multiplication . This is why we use exponents and square roots .
Although we picked 1%, we could have chosen any small unit of growth . The key is that for any rate we pick, its just a new exponent on e:
Also Check: Select Operation In Relational Algebra In Dbms
Value Of Exponential Constant
It is a significant mathematical constant and we can denote it by symbol e. Moreover, it has an approximate value equal to 2.718. Furthermore, we frequently use to model physical and economic phenomena, mathematically, where it is convenient to write e. In addition, we can easily describe the exponential function using this constant. For example, \ thus, when the value of x arises then we can calculate the value of y.
Awards And Prize Problems
The most prestigious award in mathematics is the Fields Medal, established in 1936 and awarded every four years to up to four individuals. It is considered the mathematical equivalent of the Nobel Prize.
Other prestigious mathematics awards include:
- The Abel Prize, instituted in 2002 and first awarded in 2003
- The Chern Medal for lifetime achievement, introduced in 2009 and first awarded in 2010
- The Wolf Prize in Mathematics, also for lifetime achievement, instituted in 1978
A famous list of 23 open problems, called “Hilbert’s problems“, was compiled in 1900 by German mathematician David Hilbert. This list has achieved great celebrity among mathematicians, and, as of 2022, at least thirteen of the problems have been solved.
A new list of seven important problems, titled the “Millennium Prize Problems“, was published in 2000. Only one of them, the Riemann hypothesis, duplicates one of Hilbert’s problems. A solution to any of these problems carries a 1 million dollar reward. To date, only one of these problems, the Poincaré conjecture, has been solved.
You May Like: What Is The Definition Of Potential Energy In Physics
Use Eulers Constant To Calculate Compounding Interest
Because e is related to exponential relationships, the number is useful in situations that show constant growth.
One common example, which Bernoulli explored, is related to compound interestthe interest you pay on a loan when you include both the initial principal and accumulated interest over previous periods in the calculation. Its why you can make a minimum payment on your credit card every month, yet never pay it off in full.
Suppose you put some money in the bank, and the bank compounds that money annually at a rate of 100 percent. After one year, youd have twice the amount you invested.
Now suppose the bank compounds the interest every 6 months, but only offers half the interest rate, or 50 percent. In this case, youd end up with 2.25 times your initial investment after one year.
Lets keep going. Suppose the bank offered 8.3 percent interest compounded every month, or 1.9 percent interest compounded every week. In that case, youd make 2.61 and 2.69 times your investment.
Lets write an equation for this. If we make n equal to the number of times that interest is compounded, then the interest rate is the reciprocal, or 1/n. The equation for how much money youd make in a year is n. For example, if your interest is compounded five times per year, youd make 5 = 5 = 5 = 2.49 times your initial investment.
Hard Math Problems
What Else Can You Do with Eulers Constant?
Equations for waves in physics.
Footnote: More About Liouville Numbers
A Liouville Number is a special type of transcendental number which can be very closely approximated by rational numbers.
More formally a Liouville Number is a real number x, with the property that, for any positive integer n, there exist integers p and q such that:
Now we know that x is irrational, so there will always be a difference between x and any p/q: so we get the “0< ” part.
But the second inequality shows us how small the difference is. In fact the inequality is saying “the number can be approximated infinitely close, but never quite getting there”. In fact Liouville managed to show that if a number has a rapidly converging series of rational approximations then it is transcendental.
Another interesting property is that for any positive integer n, there exist an infinite number of pairs of integers obeying the above inequality.
You May Like: What Is Secondary Succession In Biology
What Is Euler’s Number
The term Euler’s number refers to a mathematical expression for the base of the natural logarithm. This is represented by a non-repeating number that never ends. The first few digits of Euler’s number are 2.71828. The number is usually represented by the letter e and is commonly used in problems relating to exponential growth or decay. You can also interpret Euler’s number as the base for an exponential function whose value is always equal to its derivative. In other words, e is the only possible number such thatexincreases at a rate ofexfor every possible x.
Relation To More General Exponential Functions
The exponential function x } is sometimes called the natural exponential function for distinguishing it from the other exponential functions. The study of any exponential function can easily be reduced to that of the natural exponential function, since per definition, for positive b,
As functions of a real variable, exponential functions are uniquely characterized by the fact that the derivative of such a function is directly proportional to the value of the function. The constant of proportionality of this relationship is the natural logarithm of the base b:
For b> 1, the function b is increasing , because ln 0 makes the derivative always positive while for b< 1, the function is decreasing and for b = 1 the function is constant.
Euler’s numbere = 2.71828… is the unique base for which the constant of proportionality is 1, since ln , so that the function is its own derivative:
This function, also denoted as exp x, is called the “natural exponential function”, or simply “the exponential function”. Since any exponential function can be written in terms of the natural exponential as b b =e^} , it is computationally and conceptually convenient to reduce the study of exponential functions to this particular one. The natural exponential is hence denoted by
The former notation is commonly used for simpler exponents, while the latter is preferred when the exponent is a complicated expression.
n
You May Like: Holt Algebra 2 Powerpoint Presentations
What Does An E At The End Of A Number Mean
Uppercase “E” stands for “exponent” in calculator displays. Calculator manufacturers use it to display numbers in scientific notation because the longhand version is difficult to display and would be even more difficult to read. To complicate matters, some calculator manufacturers use lowercase “e” to denote exponents, inviting confusion between scientific notation and Euler’s number, which is a different thing altogether. Don’t be taken in. If either an uppercase or lowercase letter “e” appears on your display, it denotes an exponent. The only place you’ll see Euler’s number is on the keypad.
TL DR
On a calculator display, E stands for exponent of 10, and it’s always followed by another number, which is the value of the exponent. For example, a calculator would show the number 25 trillion as either 2.5E13 or 2.5e13. In other words, E is a short form for scientific notation.
Justification #: The Series Method
By use of Taylors Theorem, we can show the following to be true for all real numbers:
sin x = x – x3/3! + x5/5! – x7/7! + x9/9! – x11/11! + …cos x = 1 – x2/2! + x4/4! – x6/6! + x8/8! – x10/10! + …ex = 1 + x + x2/2! + x3/3! + x4/4! + x5/5! + x6/6! + x7/7! + x8/8! + x9/9! + x10/10! + x11/11! + …
Knowing that, we have a mechanism to determine the value of ei, because we can express it in terms of the above series:
e^(
Recommended Reading: How Much Is Math Tutoring Per Hour
Expressing Exponents On A Calculator
In its written form, scientific notation would look strange on a calculator. It would be confusing and it wouldn’t fit on a small display. To avoid these problems, manufacturers created a symbol for “X 10.” This symbol is either E or e, depending on the calculator. This letter is always followed by a number, which is the exponent to which 10 is raised.
On a calculator display, the mass of the earth would be shown as 5.97E24 . The number 5.97 is the argument and the number 24 is the exponent. Similarly, the mass of a hydrogen atom would be 1.67E-27 .
Difference Between Equal And Equivalent Sets
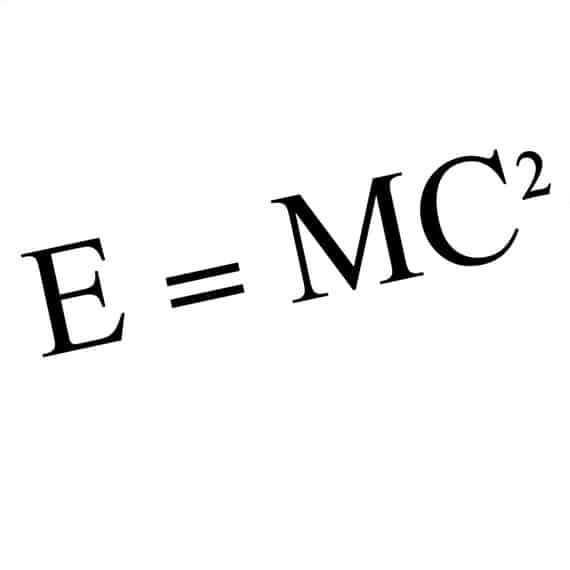
The table given below highlights the similarities and differences between equal and equivalent sets:
| Equal Sets | Equivalent Sets |
|---|---|
| If all elements are equal in two or more sets, then they are equal. | If the number of elements is the same in two or more sets, then are equivalent. |
| Equal sets have the same cardinality | Equivalent sets have the same cardinality. |
| They have the same number of elements. | They have the same number of elements. |
| The symbol used to denote equal sets is ‘=’ | The symbol used to denote equivalent sets is ~ or |
| All equal sets are equivalent sets. | Equivalent sets may or may not be equal. |
| Elements should be the same. | Elements need not be the same. |
Important Properties of Equal Sets
- Equal sets are equivalent but equivalent sets need not be equal.
- Sets with the same elements are equal.
- If two sets are subsets of each other, then they are equal.
Related Topics
Recommended Reading: Common Core Algebra 1 Unit 10 Lesson 6
Statistics And Other Decision Sciences
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially probability theory. Statisticians “create data that makes sense” with random sampling and with randomized experiments the design of a statistical sample or experiment specifies the analysis of the data . When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians “make sense of the data” using the art of modelling and the theory of inferencewith model selection and estimation the estimated models and consequential predictions should be tested on new data.
Statistical theory studies such as minimizing the risk of a statistical action, such as using a procedure in, for example, parameter estimation, hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing an objective function, like expected loss or cost, under specific constraints: For example, designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence. Because of its use of optimization, the mathematical theory of statistics overlaps with other , such as operations research, control theory, and mathematical economics.
History Of Euler’s Number
Although commonly associated with and named after the Swiss mathematician Leonhard Euler, it was first discovered in 1683 by mathematician Jacob Bernoulli. He was trying to determine how wealth would grow if interest were compounded more often, instead of on an annual basis.
The most pivotal work surrounding the number was not performed until several decades later, by Leonhard Euler. In his book Introductio in Analysin Infinitorum , Euler proved that it was an irrational number, whose digits would never repeat. He also proved that the number can be represented as an infinite sum of inverse factorials:
e n ! e = 1 + \frac + \frac + \frac + \frac + … + \frac e=1+11+21+1×2×31+1×2×3×41+…+n!1
Euler used the letter efor exponents, but the letter is now widely associated with his name. It is commonly used in a wide range of applications, including population growth of living organisms and the radioactive decay of heavy elements like uranium by nuclear scientists. It can also be used in trigonometry, probability, and other areas of applied mathematics.
Euler’s number should not be confused with Euler’s constant, which is denoted by the lower case gamma . Also known as the Euler-Mascheroni constant, the latter is related to harmonic series and has a value of approximately 0.57721….
Don’t Miss: How To Make Someone Fall In Love With You Psychology
What Does E Equal To
The value of e to the x is equal to \
Because of such an infinite value, the technique of round-off and approximation becomes essential. Furthermore, e is the base of the natural logarithm and we use it in the natural exponential function:
- ex = e power of x.
E is the limit of \^n\) as n approaches infinity, and we can calculate it as the sum of the infinite series.
You can use this free online log calculator that help to calculate logs and inverse log of any number base.
Differentiation Of E To The Power X Using Derivative Of Ax
An exponential function is of the form f = ax, where ‘a’ is a constant and x is the variable. The derivative of exponential function f = ax is f’ = ax. Using this formula and substituting the value a = e in f’ = ax, we get the differentiation of e to the power x which is given by f’ = ex = 1 × ex = ex . Hence, the derivative of e to the power x is ex.
Important Notes on Differentiation of e to the Power x:
- The nth differentiation of e to the power x is equal to ex, that is, dn/dxn = ex
- The derivative of the exponential function with base e is equal to ex.
- The derivative of eax is aeax. Using this formula, we have the differentiation of ex to be 1.ex = ex.
Related Topics:
Read Also: What Does Mks Stand For In Physics
What Is Eulers Constant
Eulers constantwhich youll also see some math experts refer to as Eulers numberis an irrational number, meaning you cant reduce it to a simple fraction. Just like pi, es decimals go on forever without repeating. If you want to get technical, this is what e looks like to the 100th decimal point:
2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274…
If youve ever taken an entry level calculus course, youve probably run into Eulers constant, since its the base for the natural logarithms. It looks like this: eln x= x.
While graphing the equation y=ex, youll find the slope of that curve at any given point is also ex, and the area under the curve from negative infinity up to x is alsoex. Eulers constant is the only number in all of mathematics that can be plugged into the equation y=nx for which this pattern is true.