What Is An Algebraic Expression
Many people interchangeably use algebraic expressions and algebraic equations, unaware that these terms are totally different.
An algebraic is a mathematical phrase where two sides of the phrase are connected by an equal sign . For example, 3x + 5 = 20 is an algebraic equation where 20 represents the right-hand side , and 3x +5 represents the left-hand side of the equation.
On the other hand, an algebraic expression is a mathematical phrase where variables and constants are combined using the operational symbols.; An algebraic symbol lacks the equal sign.;For example, 10x + 63 and 5x 3 are examples of algebraic expressions.
Lets take a review of the terminologies used in an algebraic expression:
- A variable is a letter whose value is unknown to us. For example, x is our variable in the expression: 10x + 63.
- The coefficient is a numerical value used together with a variable. For example, 10 is the variable in the expression 10x + 63.
- A constant is a term that has a definite value. In this case, 63 is the constant in an algebraic expression, 10x + 63.
There are several types of algebraic expressions, but the main type includes:
- Monomial algebraic expression
This type of expression has only one term, for example, 2x, 5x 2 ,3xy, etc.
- Binomial expression
An algebraic expression having two, unlike terms, for example, 5y + 8, y+5, 6y3 + 4, etc.
- Polynomial expression
Other types of algebraic expressions are:
- Numeric Expression:
- Variable Expression:
Why Is Algebra So Hard
Algebra is thinking logically about numbers rather than computing with numbers. Paradoxically, or so it may seem, however, those better students may find it harder to learn algebra. Because to do algebra, for all but the most basic examples, you have to stop thinking arithmetically and learn to think algebraically.
What Are The 3 Types Of System Of Linear Equation
There are three types of systems of linear equations in two variables, and three types of solutions.
- An independent system has exactly one solution pair. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution.
- A dependent system has infinitely many solutions.
Recommended Reading: Segment Addition Postulate Find The Length Indicated
How Do You Simplify Bodmas
These letters stand for vinculum, bracket, of, division, multiplication, addition and subtraction respectively. The sums on simplification must be solved in that order i.e., first solve vinculum followed by bracket and so on until the sum is solved. In simplifying an expression first of all bar must be removed.
Example: Ax2 + Bx + C

- a and b are coefficients
- c is a constant
An Operator is a symbol that shows an operation .
A Term is either a single number or a variable, or numbers and variables multiplied together.
An Expression is a group of terms
So, now we can say things like “that expression has only two terms”, or “the second term is a constant”, or even “are you sure the coefficient is really 4?”
You May Like: Eoc Fsa Warm Ups Algebra 1 Answers
How To Simplify Math Expressions
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 16 people, some anonymous, worked to edit and improve it over time. This article has been viewed 273,965 times.Learn more…
Math students are often asked to give their answer in “the simplest terms”in other words, to write answers as small as possible. Though a long, ungainly expression and a short, elegant one may technically equal the same thing, often, a math problem isn’t considered “done” until the answer has been reduced to simplest terms. In addition, answers in simplest terms are almost always the easiest expressions to work with. For these reasons, learning how to simplify expressions is a crucial skill for aspiring mathematicians.
Unlock This Answer Now
Start your 48-hour free trial to unlock this answer and thousands more. Enjoy eNotes ad-free and cancel anytime.
Already a member? Log in here.
9x is a term.; 9 is the number part and is called a coefficient.; x is the letter part and is called a variable.; When;a coefficient is combined with a variable, a term is form:; 9x
9x and 3x are considered like terms because they both have the same variable.; Like terms can be combined by adding the coefficients of the terms.; The variable does not change.
9x + 3x = 12x
Recommended Reading: Math Caching
How Do You Check Algebra Answers
Actually plugging in your answer requires you to go through the algebra manipulations in the problem. You add, subtract, multiply, and divide to see if you get a true statement using your answer. For example, you need to perform the operations in the following equation after plugging in your answer for the variable x.
What Is A Coefficient
A coefficient refers to a;number or quantity placed with a variable.;It is usually an integer that is multiplied by the variable next to it. The variables which do not have a number with them are assumed to be having 1 as their coefficient. For example, in the;expression 3x,;3;is the coefficient but in the expression x2;+ 3, 1 is the coefficient of x2. In other words, a coefficient is a multiplicative factor in the terms of a polynomial, a series, or any expression. It is generally;a number.;Observe the following expression which shows that 5 is the coefficient of x2 and 8 is the coefficient of y.
Also Check: Angle Addition Postulate Practice
How To Solve Algebraic Expression
The purpose of solving an algebraic expression in an equation is to find the unknown variable. When two expressions are equated, they form an equation, and therefore, it becomes easier to solve for the unknown terms.
To solve an equation, place the variables on one side and the constants on the other side. You can isolate the variables by applying arithmetic operations like addition, subtraction, multiplication, division, square root, cube root, etc.
An algebraic expression is always interchangeable. This implies that you can rewrite the equation by interchanging the LHS and RHS.
Calculate the value of x in the following equation
5x + 10 = 50
Given Equation as 5x + 10 = 50
- Isolate the variables and the constants;
- You can keep the variable on the LHS and the constants on the RHS.
5x = 50-10
What Is The Composition Of Two Functions
In mathematics, function composition is an operation that takes two functions f and g and produces a function h such that h = g). In this operation, the function g is applied to the result of applying the function f to x. Intuitively, if z is a function of y, and y is a function of x, then z is a function of x.
Recommended Reading: How Many Questions Can You Miss On The Ged Math Test To Pass
What Does 3x Mean In Algebra
Some terms contain variables with a number in front of them. The number in front of a term is called a coefficient. Examples of single terms: 3x is a single term. The 3 is a coefficient. The x is the variable.
It means that she earns 3x of what you earn. So, if you earn $100, she earns $400. She earns three times as much as I. This means that if you have $100, she earns $300. If you earn X dollars, three times more than x means 3x + x more than means add.
How Do You Add A Function
Operations on Functions: Adding and Subtracting Functions
Read Also: What Is Mean Median Mode And Range In Math
What Does A Mini Circle Between F And H Mean
I am currently doing a math problem and have come across an unfamiliar notation.A mini circle between $f$ and $h$
The question ask me to find for ‘the functions $f=2x-1$ and $h=3x+2$’
$$f \circ h$$
However, I can’t do this as I do not know what the circle notation denotes to.Does it mean to multiply?
This notation means that you take the output of $h$ and use it as the input of $f$. When we are working with a specific $x$ value, we can suggestively write $f)$ instead.
For instance if $f=1/z$ and $h=2+3x$ then $$ = f\big\big) = f = \frac.$$
The circle $\circ$ is the symbol for composition of functions. In General, if you have two functions $g\colon X\rightarrow Y$ and $f\colon Y\rightarrow Z$, then$f\circ g$ is a function from $X$ to $Z$. For $x\in X$ one has $ = f)$.
In your case one has: $f = 2x-1$, $g = 3x+2$ and $$ = f) = 2)-1 = 2 -1 = 6x+3.$$You take the function $g$ and put it in place of the $x$ in the function $f$.
This is obviously different from $f\cdot g = \cdot = 6x^2+x-2$.
A Close Look At The Math Behind Leveraged Etf Returns
An Application of the Geometric and Arithmetic Means
Over the past several years there has been a proliferation of ETFs for every imaginable purpose.
One particularly interesting type of ETF is the leveraged ETF. These ETFs are designed to provide 2X or 3X the daily return of a target index such as the S&P500, and they do a reasonable job of achieving this goal.
For example, if the S&P500 is up 1% for the day, the 2X S&P500 fund will be up 2% and the 3X fund will be up 3%. If the S&P500 is down 0.5% for the day, then the 2X fund will be down 1% and the 3X fund will be down 1.5%. .
Based on this description, you might think that if the S&P500 is up 10% for the year, then the 2X S&P500 fund would be up 20% and the 3X S&P500 fund will be up 30%. However, this is not the case. In fact, under some conditions, the 2X and 3X leveraged funds may be up even less than the S&P500 index. How can this be? If the daily leveraged returns are 2X or 3X the returns of the target fund, then why wont the annual returns be 2X or 3X the annual returns?
To understand why there is discrepancy between daily returns and long-term returns, we need to review the difference between the arithmetic and geometric means.
Arithmetic Mean
The arithmetic mean is what most of us think of when we hear the term average, and it is defined by this equation.
Geometric Mean
The geometric mean is the nth root of the product of n numbers, and it is defined by this equation:
Application to Leveraged ETFs
Don’t Miss: What Is Mean Median Mode And Range In Math
How Do You Solve 3 Equations With 2 Variables
Is Direxion A Good Investment
These Direxion ETFs can deliver big short-term gains, but they are trades, not investments. Direxion is one of the largest issuers of leveraged exchange-traded funds , those products that have the power to seduce with the potential for outsized short-term gains but can also be ruinous if held for too long.
You May Like: Geometry Segment Addition Postulate Worksheet
What Are Graniteshares 3x
GraniteShares 3x Long Rolls-Royce Daily ETP is a collateralised, Exchange-Traded Product . It tracks, excluding fees and other adjustments, the performance of the Solactive Daily Leveraged 3x Long Rolls-Royce Holdings plc Index that seeks to provide 3 times the daily performance of Rolls-Royce Holdings plc shares.
Examples On Multiplying Functions F G:
Ex 1: Multiply the given two functions and .
Sol:
Now, f = , g =
f * g = ;= x3 + +
= + +
= x5 + 3×4 x3 2×4 6×3 + 2×2 4×2 12x + 4
= x5 + x4 7×3 + 2×2 12x + 4.
Ans: The last answer is x5 + x4 7×3 + 2×2 12x + 4.
Ex 2:Multiply the given two functions and .
Sol:; f = ,; g =
f * g= ; = x + 7
= x3 + x2 + 7×2 + 7x
Ans:; The last answer is x3 + 8×2 + 7x.
Ex 3: Multiply the given two functions and
Sol: Given f = and g =
Multiply the above functions, we get
= 3x 5
= 3×2 + 3×3 9x 5x 5×2 + 15
= 3×3 2×2 14x + 15
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
How The Constants Are Declared
You use the Const statement to declare a constant and set its value. By declaring a constant, you assign a meaningful name to a value. Once a constant is declared, it cannot be modified or assigned a new value. You declare a constant within a procedure or in the declarations section of a module, class, or structure.
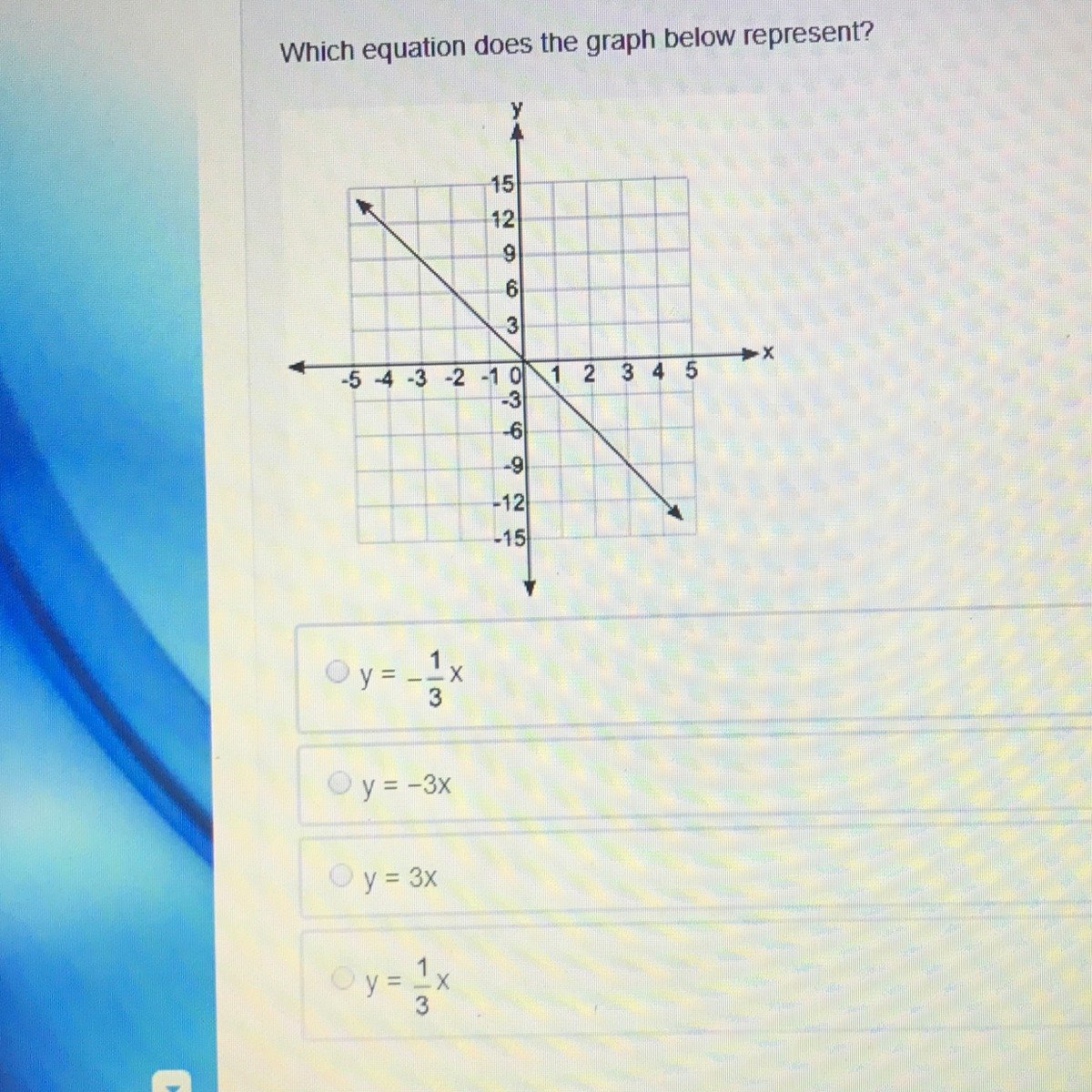
Is Y 2x 3 A Linear Equation
Explanation: y=2×3 is in slope intercept form for a linear equation, y=mx+b , where m is the slope and b is the y-intercept. The y-intercept is the point at which x=0 and y=3 , which is point You can plot this point on your graph. The slope is can be described as riserun , and can be written as 21 .
You May Like: What Is The Molecular Geometry Of Ccl4
What Is Composition And Types
Key Takeaways. In writing, composition refers to the way a writer structures a piece of writing. The four modes of composition, which were codified in the late 19th century, are description, narration, exposition, and argumentation. Good writing can include elements of multiple modes of composition.
What Does E Mean In Math
The letter E can have two different meaning in math, depending on whether it’s a capital E or a lowercase e. You usually see the capital E on a calculator, where it means to raise the number that comes after it to a power of 10. For example, 1E6 would stand for 1 × 106, or 1 million. Normally, the use of E is reserved for numbers that would be too long to be displayed on the calculator screen if they were written out longhand.
Mathematicians use the lowercase e for a much more interesting purpose to denote Euler’s number. This number, like , is an irrational number, because it has a non-recurring decimal that stretches to infinity. Like an irrational person, an irrational number seems to make no sense, but the number that e denotes doesn’t have to make sense to be useful. In fact, it’s one of the most useful numbers in mathematics.
Recommended Reading: Lesson 9.5 Geometry Answers
Euler’s Number In Nature
Exponents with e as a base are known as natural exponents, and here’s the reason. If you plot a graph of
you’ll get a curve that increases exponentially, just as you would if you plotted the curve with base 10 or any other number. However, the curve y = ex has two special properties. For any value of x, the value of y equals the value of the slope of the graph at that point, and it also equals the area under the curve up to that point. This makes e an especially important number in calculus and in all the areas of science that use calculus.
The logarithmic spiral, which is represented by the equation
is found throughout nature, in seashells, fossils and and flowers. Moreover, e turns up in numerous scientific contexts, including the studies of electric circuits, the laws of heating and cooling, and spring damping. Even though it was discovered 350 years ago, scientists continue to find new examples of Euler’s number in nature.
Related Articles
How Do You Solve Two Linear Equations With Two Variables
Solving Systems of Equations in Two Variables by the Addition Method
You May Like: What Is The Molecular Geometry Of Ccl4
E In Scientific Notation And The Meaning Of 1e6
You don’t need a calculator to use E to express a number in scientific notation. You can simply let E stand for the base root of an exponent, but only when the base is 10. You wouldn’t use E to stand for base 8, 4 or any other base, especially if the base is Euler’s number, e.
When you use E in this way, you write the number xEy, where x is the first set of integers in the number and y is the exponent. For example, you would write the number 1 million as 1E6. In regular scientific notation, this is 1 × 106, or 1 followed by 6 zeros. Similarly 5 million would be 5E6, and 42,732 would be 4.27E4. When writing a number in scientific notation, whether you use E or not, you usually round to two decimal places.
Related Articles To Coefficient
Also Check: Holt Geometry Lesson 4.5 Practice B Answers