Relational Algebra In Sql
Here relational algebra in SQL has some query in which use to retrieve the data together with the condition. Such as we know discuss all query SQL in the above all section with the example in brief.
Here Actually relational algebra and SQL methods, both are the same but there implementation different. In this case, we used the query of SQL Such as when retrieving the data.
Select Ename from Employee, Department Where Employee.Eno = Department.Eno Select Ename from Employee Natural Join Department
A Quick Introduction To Relational Algebra Operators With Examples
Database management systems must have a query language so that the users can access the data stored in the database. Relational algebra is considered as a procedural query language where the user tells the system to carry out a set of operations to obtain the desired results. i.e. The user tells what data should be retrieved from the database and how to retrieve it. In this article, I will give a brief introduction to relational algebra and go through a few operations with examples and PostgreSQL commands.
Cartesian Product In Dbms
Cartesian Product in DBMS is an operation used to merge columns from two relations. Generally, a cartesian product is never a meaningful operation when it performs alone. However, it becomes meaningful when it is followed by other operations. It is also called Cross Product or Cross Join.
Example Cartesian product
column 2 = 1
Output The above example shows all rows from relation A and B whose column 2 has value 1
| column 2 = 1 |
|---|
| column 1 |
Join operation is essentially a cartesian product followed by a selection criterion.
Join operation denoted by .
JOIN operation also allows joining variously related tuples from different relations.
Types of JOIN:
Various forms of join operation are:
Inner Joins:
- Full Outer Join
Read Also: Age Word Problem With Solution
Va12composition Of Relational Algebra Operations And Renaming
As we have seen, each relational algebra operation results in another relation, a property called closure. The resulting relation could therefore have been used to perform a second relational algebra operation, giving a sequence of two operations. In fact, we can carry out a sequence of several operations, each of which is performed using the result of the previous one. For example, using Figure 1, suppose we wished to find the names of all Customers who have ordered item I1004. We can see from the Order table that only the first tuple involves I1004. Choosing rows that have a specified value is a SELECT operation, so we write
for that part of the query. Once we have found the tuple or tuples having the correct itemNo value, we do a natural join with the Customer table to find the corresponding customer records. We indicate that the join is to be performed with the previous result by writing
Finally, we find the custName by applying a projection to this result, so that the entire expression becomes
It is permissible to assign names to the intermediate results, a process called renaming, by a simple statement such as
-
AND T1.sale_id = sale.sale_id
-
AND sale.customer_numb = customer.customer_numb
If you use the SQL-92 join syntax, then you have some control over the order in which the joins are performed:
-
SELECT first_name, last_name
Jan L. Harrington, in, 2009
Operators In Relational Algebra

As we have already discussed why we used them, it is basically used in the procedural query language, and we have several types of operations available, Relational Algebra, in this section we will discuss majorly on the types we have with their subtype define. So lets take a closer look at various types available, see below
Recommended Reading: Who Are Paris Jackson’s Biological Parents
Joins Operation In Relational Algebra
Join operation in relational algebra is a combination of a Cartesian product followed by which satisfy certain condition. A Join operation combines two tuples from two different relations, if and only if a given condition is satisfied.
There are different types of join operations.
Natural Join
A result of natural join is the set of tuples of all combinations in R and S that are equal on their common attribute names.
It is denoted by .
Consider the following example to understand natural Joins.
EMPLOYEE
| Sports |
- Equi Join
When Theta join uses equality operator for comparison, then it is called equi join. The above example of theta join is applicable for equi join.
Relational Algebra Operations In Dbms
Different relational algebraoperationsin dbms are as below:
Selection operation in relational algebra is used to find the tuples in a relation which satisfy the given condition. It is denoted by sigma .
Notation p
Where indicates selection predicate and r denotes relation and p is a propositional logic formula which may use relational operators like and, or, and not.
account_type = saving
Output It selects tuples from relation Account where the account type is saving.
2.Project Operation
Project or projection operation in dbms relational algebra is used to select required attributes or columns from relation. Symbol indicates Project operation.
Notation Attr1, Attr2, Attrn
Where Attr1, Attr , Attrn are attribute of relation r.
Stud_rollno, name, city
Output It selects attributes stud_rollno, name and city from relation Student
Read Also: Eoc Fsa Practice Test Algebra 1
Implementing Other Set Operations
The customary way to implement the set operations of UNION , INTERSECTION and DIFFERENCE is to sort the two relations on the same attributes. After sorting, a single scan through each relation is sufficient to produce the result. For example, we can implement R UNION S by scanning both stored files concurrently, and whenever we encounter the same tuple on both relations we keep only one of those in the result. For R INTERSECT S, we keep in the result only the tuples that appear in both relations. If sorting is done on unique key attributes, the operations are further simplified.
Hashing can also be used to implement UNION , INTERSECTION and DIFFERENCE by hashing both files to the same hash file buckets. For example, to implement R UNION S, we first hash the records of R to the hash file then, while hashing the records of S, we do not insert duplicate records.
Why Study Relational Algebra
We define data manipulation as a relational algebra not just to support data retrieval but also to allow the writing of expressions , which in turn can be used for retrieval, for defining scope for updates, for defining virtual data, which may form part of a users view, for defining access rights, integrity, etc.
Thus expressions are a high-level symbolic representation, which can be subject to transformation rules to get equivalent expressions – this in essence means that relational algebraic expressions are a convenient basis for query optimization.
Knowing relational algebra leads to a better understanding of what the DBMS does for us when we submit SQL queries for processing. It explains conceptually how the data for the query is actually retrieved from the tables. Since there are often several different and correct ways to write an query to get the data we need, it becomes important for us to know which way might result is faster processing time. It also assists with an understanding of the concepts behind the important topic of query optimization.
Recommended Reading: How To Calculate Half Life Chemistry
Students Who Viewed This Also Studied
Krishna Institute Of Engineering and Technology
CSE DBMS
Krishna Institute Of Engineering and Technology
CSE DBMS
Krishna Institute Of Engineering and Technology
CSE DBMS
Krishna Institute Of Engineering and Technology
CSE DBMS
Krishna Institute Of Engineering and Technology CSE DBMS
Recovery.ppt
Krishna Institute Of Engineering and Technology CSE DBMS
transaction_Unit4.ppt
Krishna Institute Of Engineering and Technology CSE DBMS
Relational Calculus.pptx
Krishna Institute Of Engineering and Technology CSE DBMS
Assignment-3.doc
Relational Algebra In Dbms
by Neha T
Relational algebra is query language based on the set theory of mathematics. It is procedural as it defines the sequence in which the query must be operated to retrieve the result. Relational algebra has some basic fundamental operators along with some derived operators.
In this section, we will discuss the definition of relational algebra. We will study each operator along with an example and we will conclude the content by discussing the advantages and limitations of relational algebra.
You May Like: My Hrw Com Algebra 1
What Is The Difference Between Select And Project Operations
I’m referring to the basic relational algebra operators here.As I see it, everything that can be done with project can be done with select.
I don’t know if there is a difference or a certain nuance that I’ve missed.
- 7Herbalessence’s answer is totally correct, but the basic idea is: with the selection operator you specify which rows you want, with the projection operator you specify which columns you want.Mar 25 ’11 at 18:08
- 3Please note that this question is about relational algebra operators as opposed to SQL’s SELECT statement. Read @EmergeStronger’s answer for a clearer explanation of the differences. shrmnDec 1 ’15 at 1:53
- Selecting means choosing some records from a table and leaving others out. Projecting means choosing some columns from each record and leaving others out
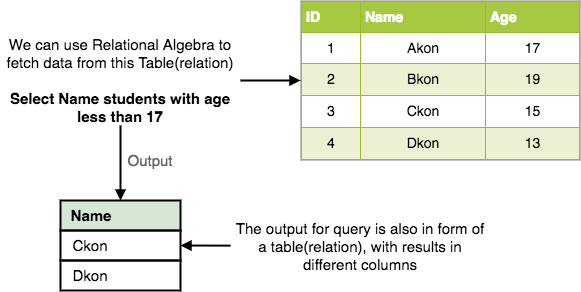
Select Operation : This operation is used to select rows from a table that specifies a given logic, which is called as a predicate. The predicate is a user defined condition to select rows of user’s choice.
Project Operation : If the user is interested in selecting the values of a few attributes, rather than selection all attributes of the Table , then one should go for PROJECT Operation.
In Relational algebra ‘Selection’ and ‘Projection’ are different operations, but the SQL SELECT combines these operations in a single statement.
Select retrieves the tuples in a relation for which the condition in ‘predicate’ section stands true.
Project retrieves the attributes specified.
What Is Relational Algebra In Dbms
Relational algebra is a procedural query language that works on relational model. The purpose of a query language is to retrieve data from database or perform various operations such as insert, update, delete on the data. When I say that relational algebra is a procedural query language, it means that it tells what data to be retrieved and how to be retrieved.
On the other hand relational calculus is a non-procedural query language, which means it tells what data to be retrieved but doesnt tell how to retrieve it. We will discuss relational calculus in a separate tutorial.
Read Also: Geometry Segment Addition Postulate Worksheet
Making Vertical Subsets: Project
The first relational algebra operation we will consider is one that is used by every SQL query that retrieves data: project. A projection of a relation is a new relation created by copying one or more the columns from the source relation into a new table. As an example, consider Figure 6.2. The result table is a projection of the customer relation, containing the attributes customer_numb, first_name, and last_name.
Figure 6.2. Taking a projection.
Using the syntax for relational algebra, the projection in Figure 6.2 is written:
The order of the columns in the result table is based on the order in which the column names appear in the project statement the order in which they are defined in the source table has no effect on the result. Rows appear in the order in which they are stored in the source table project does not include sorting or ordering the data in any way. As with all relational algebra operations, duplicate rows are removed.
Note: It is important to keep in mind that relational algebra is first and foremost a set of theoretical operations. A DBMS may not implement an operation the same way that it is described in theory. For example, most DBMSs dont remove duplicate rows from result tables unless the user requests it explicitly. Why? Because to remove duplicates the DBMS must sort the result table by every column , and then scan the table from top to bottom, looking for the duplicates. This can be a very slow process if the result table is large.
Explain The Select Operation In Relational Algebra
Query is a question or requesting information. Query language is a language which is used to retrieve information from a database.
Query language is divided into two types
-
Procedural language
Information is retrieved from the database by specifying the sequence of operations to be performed.
For Example Relational algebra.
Structure Query language is based on relational algebra.
Relational algebra consists of a set of operations that take one or two relations as an input and produces a new relation as output.
Recommended Reading: What Are Dyes In Chemistry
Use Of Algebraic Properties For Query Optimization
- leaves are relations,
- subtrees are subexpressions.
The primary goal is to transform expression trees into equivalent expression trees, where the average size of the relations yielded by subexpressions in the tree is smaller than it was before the optimization. The secondary goal is to try to form common subexpressions within a single query, or if there is more than one query being evaluated at the same time, in all of those queries. The rationale behind the second goal is that it is enough to compute common subexpressions once, and the results can be used in all queries that contain that subexpression.
Here are a set of rules that can be used in such transformations.
What Is Relational Algebra
The relational algebra is a theoretical procedural query language which takes an instance of relations and does operations that work on one or more relations to describe another relation without altering the original relation. Thus, both the operands and the outputs are relations. So the output from one operation can turn into the input to another operation, which allows expressions to be nested in the relational algebra, just as you nest arithmetic operations. This property is called closure: relations are closed under the algebra, just as numbers are closed under arithmetic operations.
The relational algebra is a relation-at-a-time language where all tuples are controlled in one statement without the use of a loop. There are several variations of syntax for relational algebra commands, and you use a common symbolic notation for the commands and present it informally.
The primary operations of relational algebra are as follows:
- Select
It selects tuples that satisfy the given predicate from a relation.
Notation p
Here stands for selection predicate, and r stands for relation, and p is a propositional logic formula which may use connectors like and, or, and not.
predicate: This selection operation functions on a single relation R and describes a relation that contains only those tuples of R that satisfy the specified condition .
Example:
Output – It selects tuples from names where the teacher is ‘database.’
Read Also: Kendall Hunt Geometry Answer Key
Operations For Domain Computations
There is nothing in relational algebra introduced so far that would allow computations on the data domains . For example, it is not possible using only the algebra introduced so far to write an expression that would multiply the numbers from two columns, e.g. a unit price with a quantity to obtain a total price. Practical query languages have such facilities, e.g. the SQL SELECT allows arithmetic operations to define new columns in the result SELECTunit_price*quantityAStotal_priceFROMt, and a similar facility is provided more explicitly by Tutorial D‘s EXTEND keyword. In database theory, this is called extended projection.:213
Aggregation
Furthermore, computing various functions on a column, like the summing up of its elements, is also not possible using the relational algebra introduced so far. There are five aggregate functions that are included with most relational database systems. These operations are Sum, Count, Average, Maximum and Minimum. In relational algebra the aggregation operation over a schema is written as follows:
- G r ) ,G_,\ldots ,G_\ g_,f_,\ldots ,f_}\ }
where each Aj‘, 1 ⤠j ⤠k, is one of the original attributes Ai, 1 ⤠i ⤠n.
Let’s assume that we have a table named Account with three columns, namely Account_Number, Branch_Name and Balance. We wish to find the maximum balance of each branch. This is accomplished by Branch_NameGMax. To find the highest balance of all accounts regardless of branch, we could simply write GMax(
Introduction To Relational Algebra In Dbms
Relational Algebra in DBMS is mainly used in the procedural query language. In which we take relational input and produce a relation output. In short, it is used to collect the relation as the input and try to provide the result of relational occurrence as the output. The result that we get from Relational Algebra which will be a new relationship which is formed by using one or more type of relational input. Generally, it makes us of the operator to perform the query and this operator basically is binary or unary. We have different type of operations of relation algebra few of them are select, union, project etc. In the coming section of the tutorial, we can discuss more on the internal working and implementation of the Relational Algebra in DBMS for better understanding.
You May Like: Eoc Fsa Warm Ups Algebra 1 Answers
Base And Derived Relations
In a relational database, all data are stored and accessed via relations. Relations that store data are called “base relations”, and in implementations are called “tables”. Other relations do not store data, but are computed by applying relational operations to other relations. These relations are sometimes called “derived relations”. In implementations these are called “views” or “queries”. Derived relations are convenient in that they act as a single relation, even though they may grab information from several relations. Also, derived relations can be used as an abstraction layer.
A domain describes the set of possible values for a given attribute, and can be considered a constraint on the value of the attribute. Mathematically, attaching a domain to an attribute means that any value for the attribute must be an element of the specified set. The character string “ABC”, for instance, is not in the integer domain, but the integer value 123 is. Another example of domain describes the possible values for the field “CoinFace” as . So, the field “CoinFace” will not accept input values like or .