How To Find The Range Of A Cannon Ball
A cannon is positioned with a direction of 60 degrees between the ground and itself. .The shooting velocity is $800\over \sec}$. What is its range?
I didn’t really understand this question. Am I asked how further the cannon ball will go before it descends? Because if so, I should I find the highest point the cannon ball get? Should I do it by differentiating?
I would truly appreciate your assistance.
- TimbucApr 18 ’15 at 15:23
- $\begingroup$I am confused. I’ve learned so far about acceleration, velocity, gravity and how to find each one by differentiating and integrating. Maybe I need further information?$\endgroup$Apr 18 ’15 at 15:24
- 1$\begingroup$Of course you do need more! There are well known, basic formulas for this: initial velocity, some kind of air resistance , the elevation angle, etc. You must have been given these formulas…or you can find them googing in the net, of course.$\endgroup$Apr 18 ’15 at 15:26
- $\begingroup$Consider vertical and horizontal component separately. Equate time taken.$\endgroup$
In the simplest model, you are working in two dimensions, with the system of equations:
$$\frac = -g \\\frac = 0 \\y=0,y’=\sin s \\x=0,x’=\cos s$$
where $g> 0$ is acceleration due to gravity, $\theta$ is the angle of the initial velocity, and $s$ is the initial speed. Note that this model assumes no friction. When you solve you find
$$y=-\frac gt^2 + \sin s t \\x=\cos s t.$$
In projectile motion, you need to concern yourself with the two components of displacement:
What Is Range In Projectile Motion
The range of the projectile is the displacement in the horizontal direction. There is no acceleration in this direction since gravity only acts vertically. shows the line of range. Like time of flight and maximum height, the range of the projectile is a function of initial speed.
The equations of the motion are applicable separately in x-Axis and the y-Axis for finding the unknown parameters.
R = v02sin2/g
- G = acceleration due to gravity
- = angle of the initial velocity from the horizontal plane
Was this answer helpful?
Faqs On Horizontal Projectile Motion Calculator
1. What is meant by Horizontal Projectile Motion?
If a Particle is thrown nearer to the earth’s surface then it moves under constant velocity along a curved path that is directed towards center of earth. Such motion of the particle is known as Horizontal Projectile Motion.
2. What is the formula for horizontal range?
Formula for Horizontal Projectile Motion Range is given by r = V*t.
3. Write down the list of Horizontal Projectile Motion Equations?
List of Horizontal Projectile Motion Equations are as follows Range r = V*t Time of Fight t = Equation of Trajectory y = g * ² / 2 = /
4. How to use Horizontal Projectile Motion Calculator?
All you need to do is enter any two values as per the inputs and click on the calculate button to get the concerned output in no time using Horizontal Projectile Motion Calculator.
Favorite Calculators
Recommended Reading: Practice Worksheet Special Right Triangles Answers
Projectile Range Calculator Example
Let’s find out the range of the hypothetical volcanic ballistic projectiles :
In reality, the projectile motion is a much complicated phenomenon. The air resistance reduces a range of a projectile – and that’s dependent on the object volume, shape, surface smoothness, mass, etc.
Estimating The Uncertainty In Measurements
Before you combine or do anything with your uncertainty, you have to determine the uncertainty in your original measurement. This often involves some subjective judgment. For example, if youre measuring the diameter of a ball with a ruler, you need to think about how precisely you can really read the measurement. Are you confident youre measuring from the edge of the ball? How precisely can you read the ruler? These are the types of questions you have to ask when estimating uncertainties.
In some cases you can easily estimate the uncertainty. For example, if you weigh something on a scale that measures down to the nearest 0.1 g, then you can confidently estimate that there is a ±0.05 g uncertainty in the measurement. This is because a 1.0 g measurement could really be anything from 0.95 g to just under 1.05 g . In other cases, youll have to estimate it as well as possible on the basis of several factors.
Tips
-
Significant Figures:Generally, absolute uncertainties are only quoted to one significant figure, apart from occasionally when the first figure is 1. Because of the meaning of an uncertainty, it doesnt make sense to quote your estimate to more precision than your uncertainty. For instance, a measurement of 1.543 ± 0.02 m doesnt make any sense, because you arent sure of the second decimal place, so the third is essentially meaningless. The correct result to quote is 1.54 m ± 0.02 m.
Also Check: Theory Of Everything 2 All Coins
How To Calculate The Distance To The Object Using Binoculars Range Calculator
To be able to successfully calculate the distance to a given target, use the formula D = H / K, where D is the distance to the target in kilometers, H is the estimated height of the target in meters, and Kis the vertical angle of the target expressed in millimeters. Calculate the distance by first estimating the height of the target. And then measuring the horizontal angle of the target.
Range Of Error Of Measurements
While reporting the mean time of 100 pendulum oscillation with the error.What should be the should be the error range?The one which includes all the data or the shorter one one which include most of the data?And why is it so?
The data I have:$90,91,95,92$ and the least count is 1 sec.
I think the mean should be $92\pm 3$ for it includes all the data.But it is not a short range.
I calculated the standard deviation of data.It came out to be $2.16$
The standard error in the mean is indeed given by the corrected sample standard deviation divided by the square root of the number of points.
For a large sample then you can find a reasonably unbiased estimate of the sample standard deviation by dividing the sum of the variances by $N-1$ and taking the square root. This yields the figure 2.16 in your dataset. However, for $N=4$ this is unlikely to be correct. For normally distributed uncertainties, a better estimate for small $N$ is provided by division by $N-1.5$ .
Thus, in your case: The mean is 92.0
The standard deviation of the population is 2.36 and the standard error would be 2.36/2 = 1.18.
I would probably quote this as $92.0 \pm 1.2$.
Don’t Miss: Punchline Bridge To Algebra Did You Hear About
What Are The Key Components Of Projectile Motion
The key components that we need to remember in order to solve projectile motion problems are:
- Initial launch angle, \theta
- Initial velocity, \text
- Time of flight, \text
- Acceleration, \text
- Horizontal velocity, \text_\text
- Vertical velocity, \text_\text
- Displacement, \text
- Maximum height, \text
- Range, \text
How To Solve Any Projectile Motion Problem : Introducing the âToolboxâ method of solving projectile motion problems! Here we use kinematic equations and modify with initial conditions to generate a âtoolboxâ of equations with which to solve a classic three-part projectile motion problem.
Now, letâs look at two examples of problems involving projectile motion.
Absolute Vs Relative Uncertainties
Quoting your uncertainty in the units of the original measurement for example, 1.2 ± 0.1 g or 3.4 ± 0.2 cm gives the absolute uncertainty. In other words, it explicitly tells you the amount by which the original measurement could be incorrect. The relative uncertainty gives the uncertainty as a percentage of the original value. Work this out with:
So in the example above:
The value can therefore be quoted as 3.4 cm ± 5.9%.
Read Also: Geometry Chapter 4 Practice Workbook Answers Mcdougal Littell
Horizontal Projectile Motion Calculator
Horizontal Projectile Motion Calculator is a free online tool that displays the output provided any two inputs for a horizontally launched object in the blink of an eye.
Horizontal Projectile Motion Calculator: Horizontal Projectile Motion is a special case of projectile motion. If an object is launched horizontally from an elevated plane then take help of our tool to evaluate time of flight, range, equation of trajectory, etc. given any two inputs. Continue readig to learn about What is meant by Horizontal Projectile Motion, Projectile Motion Equations, Procedure on how to find projectile motion equations, etc.
Faqs On Projectile Motion Calculator
1. What factors affect projectile motion?
Three major factors that affect the projectile motion are projection angle, magintude of projection velocity, height of projection.
2. What is the formula for Maximum Height in Projectile Motion?
Formula for Maximum Height in Projectile Motion is hmax = h + V² * sin² /
3. Does weight affect a Projectile Motion?
Yes, greater the weight of an object the greater the gravity influence on it in case of a Projectile Motion. Gravity stops the upward movement thus pulling the object downwards, thus limits the vertical component of projectile.
4. What is acceleration at a Maximum Height?
At a Projectile’s maximum height the acceleration is zero.
Favorite Calculators
You May Like: Define Percent Error In Chemistry
Range Of A Projectile
| It has been suggested that this article be merged into Projectile motion. Proposed since May 2021. |
In physics, a projectile launched with specific initial conditions will have a range. It may be more predictable assuming a flat Earth with a uniform gravity field, and no air resistance.
The following applies for ranges which are small compared to the size of the Earth. For longer ranges see sub-orbital spaceflight. The maximum horizontal distance traveled by the projectile, neglecting air resistance, can be calculated as follows:
- d 0 ) }\left}
where
- d is the total horizontal distance travelled by the projectile.
- v is the velocity at which the projectile is launched
- g is the gravitational accelerationusually taken to be 9.81 m/s2 near the Earth’s surface
- is the angle at which the projectile is launched
- y0 is the initial height of the projectile
If y0 is taken to be zero, meaning that the object is being launched on flat ground, the range of the projectile will simplify to:
- d }}\sin 2\theta }
Correct Formula To Find The Range Of A Projectile Initial Velocity Initial Elevation And G
- $g$
I want to find the range of a projectile
Hours of searching have given no useful results. Those that I thought were useful turned out to be incapable of accounting for negative angles. This formula in particular returns a range of 0 if the angle is 0, which simply doesn’t make sense.
For example:
- $\begingroup$is $\theta$ an angle to the horizontal?$\endgroup$
With horizental velocity $v_x=v_0\cos\theta$ and vertical velocity $v_y=-v_0\sin\theta-gt$ and integration we see$$x=\int_0^tv_0\cos\theta\,dt=v_0\cos\theta\,t\,\,\,,\,\,\,y=\int_0^t v_y\,dy=-v_0\sin\theta\,t-\frac12gt^2$$Eliminating $t$ between them gives$$y=-\tan\theta\,x-\fracx^2$$the range $R$ is the point $$ and you may continue from here!
Edit: The solution for $h=-y_0$ and $\theta< 0$ after solving the equation$$\fracd^2+\tan\theta\,d-h=0$$is$$d=-\dfrac\sin2\theta\left$$which works for $\theta< 0$ as you wanted.
Assuming a projectile is launched at angle $\theta$ from horizontal from a height $y_0$ above the ground, where the ground is assumed to be represented by the line $y = 0.$The measurement of the angle is such that $\theta = 0$ if the projectileinitially is moving horizontally to the right, and otherwise the angle is measured in a counterclockwise direction from “horizontal to the right,”so small positive angles are upward and small negative angles are downward.
Don’t Miss: Algebra 2 Unit Test Review Edgenuity
How To Find The Range Of A Function Algebraically
Set A is called the domain of the function fSet B is the called the co-domain of the functionSet of Images of all elements in Set A is called the range i.e it is the set of values of f which we get for each and every x in the domain
Now lets see how to find the range of a function algebraically i.e without plotting the graph
How to find the range of a function algebraically
General Method is explained below. This is called inverse function technique
put y=f Solve the equation y=f for x in terms of y ,let x =g Find the range of values of y for which the value x obtained are real and are in the domain of f The range of values obtained for y is the Range of the function
This is basically how to find range of a function without graphing
Lets see fee examples with various type of functions
Examples Of Range Formula
Lets take an example to understand the calculation of Range in a better manner.
Example #1
The functions rule assigns a small drink to $1.50, a medium drink to $2.50, and a large drink to $3.50. The inputs are the drink size, and the outputs are the drink price. Therefore, the range for this function is the set of all outputs, or {$1.50, $2.50, $3.50).
Solution:
Now we need to find the range of the given function and how spread the data set is.
A range of a given function can be calculated with the help of the following steps:-
First, we need to find what is the maximum value in the data set. Maximum Value in the data set is calculated as
Then we need to find what is the minimum value in the data set. Minimum Value in the data set is calculated as
A range is calculated using the formula given below
Range = Maximum Value Minimum Value
- Range = $3.50 $1.50
- Range = $2
Example #2
Consider the set of the following data that is . We need to find the range of the given data set.
Solution:
A range of a given function can be calculated with the help of the following steps:-
First, we need to find what is the maximum value in the data set. Maximum Value in the data set is calculated as
Then we need to find what is the minimum value in the data set. Minimum Value in the data set is calculated as
A range is calculated using the formula given below
Example #3
Also Check: Which Is Harder Chemistry Or Physics
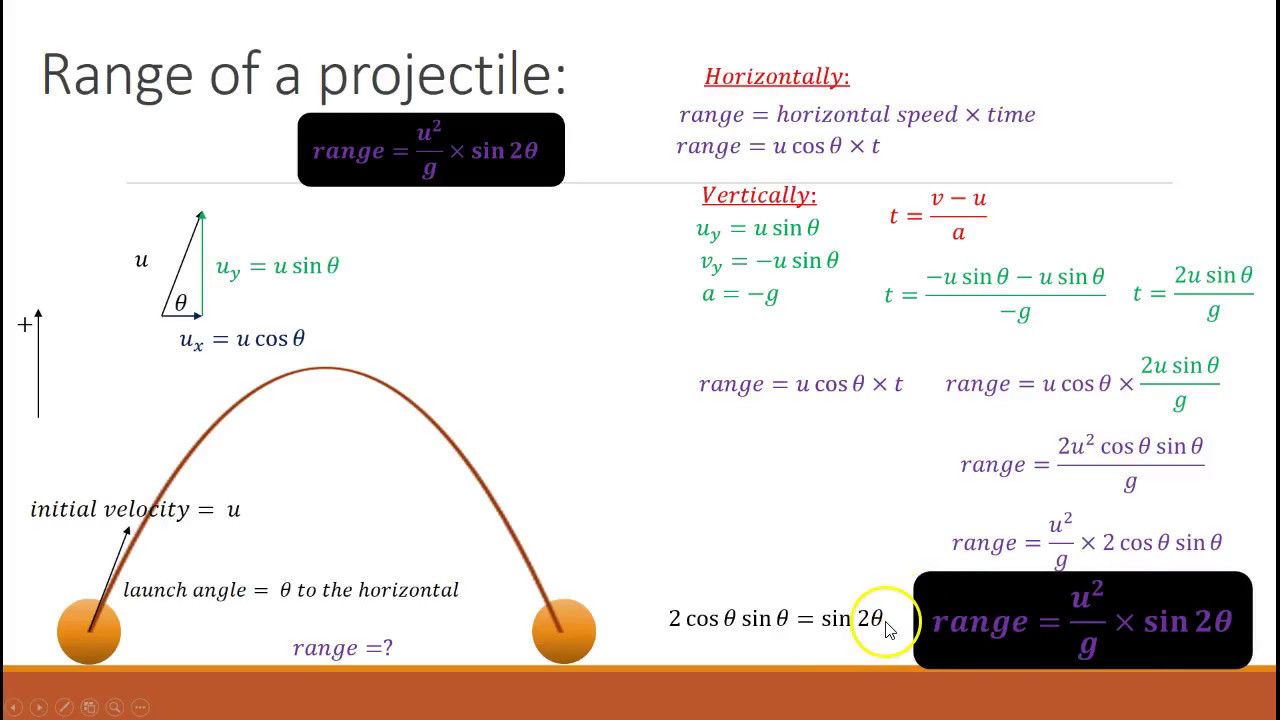
Horizontal Range Of Projectile Formula Derivation
When a projectile is launched it takes a parabolic path and the range of this parabola is given by the relation
But the question is how did we get this relation for the range of the projectile.
To derive this formula let us consider the figure given below which depicts a ball launched with initial velocity \ that makes an angle \ with the horizontal. This ball then travels in a parabola and we have to work out the range formula from this given information.
We will now break the process of our derivation into three steps for the sake of ease of learning. The summary of these steps is given below in the form of a concept map.
We know that
So, we need two things to get the formula for horizontal range
Using Elementary Mechanics To Estimate The Maximum Range Of Icbms
56
ReferencesSection:
Read Also: Half Life Of Reaction
How To Write The Range In Interval Form
| \\) | It is the open interval set between point and b such that All the pointsbetween a and b belong to the open interval but a, b themselves do not belong to this interval | \ |
| \ | It is the closed interval set between point and b such that All the pointsbetween a and b belong to the open interval including a, b | \ |
| \\) | It is the open interval set between point and b such that All the pointsbetween a and b belong to the open interval including a, but not b | \ |
| \\) | It is the open interval set between point and b such that All the pointsbetween a and b belong to the open interval including b, but not a | \ |
What Is Meant By Projectile Motion
If a particle or object is thrown nearer to the earth’s surface, the object would move towards the earth’s surface along a curved path with constant acceleration. Such path is known as trajectory or projectile and the motion is known as Projectile Motion.
Examples of Projectile Motion include throwing a cricket ball, angry bird, arrow, or stone in a river, etc. The moment you release them the only force acting on them is gravity and it creates an equal impartial acceleration.
You May Like: Introduction To Exponential Functions Algebra 1 Homework