What Does Consistent Mean In Math

What Does It Mean For A System To Be Consistent Or Inconsistent

does it stay the same or not?

Actually, a system is inconsistent if you can derive two statements within the system which are contradictory.Otherwise it is consistent.

For example, Eucliadean geometry requires that given a line anda point not on that line, you can have one and only one linethrough the point which is parallel to the original line.

However, you can have a consistent system of geometry if youassume that there is no such parallel line. This is known as theprojective plane.

You can assume that there will be an infinite number of parallellines through a point not on the line. And again you can have aconsistent system.

Consistency or inconsistency has nothing whatsoever to do withtime.

Unbiased But Not Consistent

An estimator can be unbiased but not consistent. For example, for an iid sample one can use Tn = xn as the estimator of the mean E. Note that here the sampling distribution of Tn is the same as the underlying distribution , so E = E and it is unbiased, but it does not converge to any value.

However, if a sequence of estimators is unbiased and converges to a value, then it is consistent, as it must converge to the correct value.

How Do You Calculate K Mean

K Means Clustering Select k points at random as cluster centers. Assign objects to their closest cluster center according to the Euclidean distance function. Calculate the centroid or mean of all objects in each cluster. Repeat steps 2, 3 and 4 until the same points are assigned to each cluster in consecutive rounds.

Don’t Miss: Example Of Span Linear Algebra

What Is M In A Triangle

The m in front of the angle notation refers to the measure of the angle labeled A, B and C . By definition, the term congruent means having equal length or measure. Triangles are congruent. The congruent symbol is used when referring to the actual physical entities .

Consistency And Completeness In Arithmetic And Set Theory

In theories of arithmetic, such as Peano arithmetic, there is an intricate relationship between the consistency of the theory and its completeness. A theory is complete if, for every formula in its language, at least one of or ¬ is a logical consequence of the theory.

Presburger arithmetic is an axiom system for the natural numbers under addition. It is both consistent and complete.

Gödel’s incompleteness theorems show that any sufficiently strong recursively enumerable theory of arithmetic cannot be both complete and consistent. Gödel’s theorem applies to the theories of Peano arithmetic and primitive recursive arithmetic , but not to Presburger arithmetic.

Because consistency of ZF is not provable in ZF, the weaker notion relative consistency is interesting in set theory . If T is a theory and A is an additional axiom, T + A is said to be consistent relative to T if it can be proved thatif T is consistent then T + A is consistent. If both A and ¬A are consistent with T, then A is said to be independent of T.

Read Also: K Value In Physics

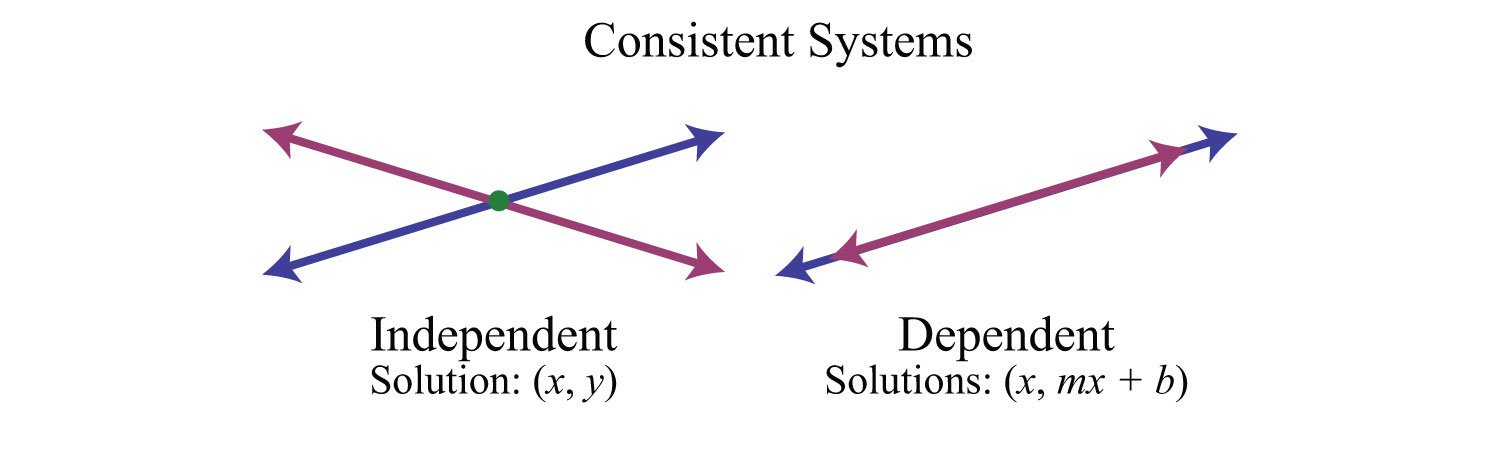
Consistent Meaning In Maths

System of linear equations is a group of two or more linear equations having the same variables. For example, x + 2y = 14 , 2x + y = 6.

To compare equations in linear systems, the best way is to see how many solutions both equations have in common. If there is nothing common between the two equations then it can be called as inconsistent. But it will be called consistent if any one ordered pair can solve both the equations. If the equation carries more than one point in common then it will be called as dependent. But what does solution in common mean? It means that if there is at least one ordered pair which can solve both the equations in spite of having many equations that dont.

For example, let us consider an equation x + y = 6 and x y = 2. Do you think they have any solutions in common? Yes, Equation x + y = 6 does have many solutions but both of the equations have one solution in common i.e., if x = 4 and y=2 then both equations have true solutions.

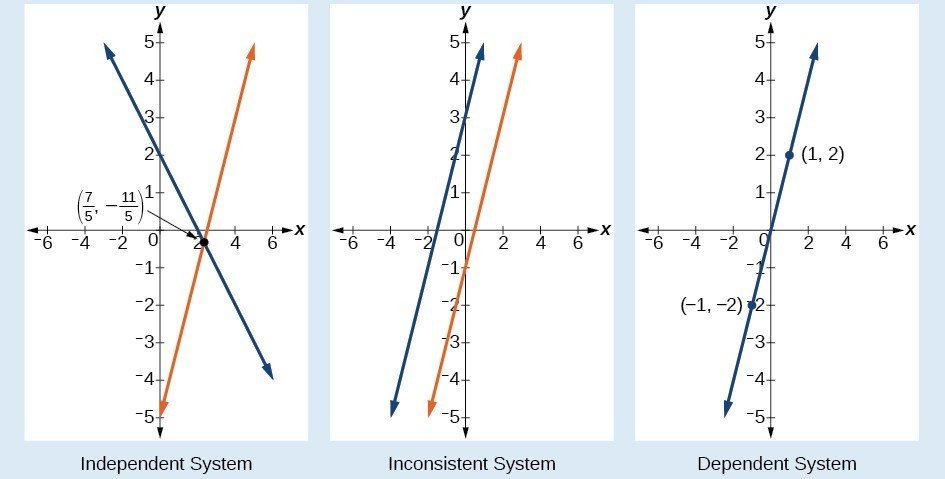
Inconsistent And Dependent Systems In Three Variables

Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as 3=7 or some other contradiction.

Read Also: Geometry Assignment Find The Length Indicated Answer Key

Webster Dictionaryrate This Definition:

What Is The Meaning Of Consistent Or Inconsistent

4.1/5Definitioninconsistentconsistentinconsistent

A system of parallel lines can be inconsistent or consistent dependent. If the lines in the system have the same slope but different intercepts then they are just inconsistent. Though if they have the same slope and intercepts then they are consistent dependent.

Secondly, what does it mean to be consistent? Someone who is consistent always behaves in the same way, has the same attitudes towards people or things, or achieves the same level of success in something. If one fact or idea is consistent with another, they do not contradict each other.

Keeping this in consideration, what does it mean for a linear system to be consistent?

In mathematics and in particularly in algebra, a linear or nonlinear system of equations is called as consistent if there is at least one set of values for the unknowns that satisfies each equation in the systemthat is, that when substituted into each of the equations makes each equation hold true as an identity.

What does consistent mean in matrices?

A system which has a solution is called consistent. If a system is inconsistent, a REF obtained from its augmented matrix will include a row of. the form 0 0 0 0 1, i.e. will have a leading 1 in its rightmost column.

Recommended Reading: Holt Geometry Workbook Answers

Princeton’s Wordnetrate This Definition:

Is Consistency An Axiom Of Mathematics

I watched the numberphile video on Gödel’s Incompleteness Theorem today, and I was wondering about something.

It seems the key to accepting the truth of Gödel’s Theorem is to demand that mathematics is consistent. However, isn’t this like invoking consistency as an axiom of mathematics? Therefore, aren’t we proving the truth of Gödel’s Theorem using the axioms? Is the consistency of mathematics something other than an axiom?

I’ve read elsewhere on here that another way to state Gödel’s theorem is to say that no formal mathematics system can prove it’s own consistency. Does that mean we just have to assume our system of mathematics is consistent?

Definitely not an expert in this!

• 27Aug 21 ’18 at 8:41
• 9$\begingroup$An inconsistent system could also have an axiom saying that the system is consistent, after all the system is inconsistent.$\endgroup$ RemcoGerlichAug 21 ’18 at 13:16
• $\begingroup$If math is inconsistent then every mathematical sentence is a theorem. ….. Godel: Let $S$ be a recursive system of axioms that is powerful enough to discuss the arithmetic of $\Bbb N.$ Then $S$ is incomplete or inconsistent.$\endgroup$

Yes. That is exactly what it means. Consistency assumptions are axioms.

This gives rise to a natural hierarchy of axioms, specifically part of set theory, called large cardinal axioms which are stronger and stronger in consistency strength, and generally each one implies the weaker are consistent .

And the list continues.

A few more comments.

You May Like: Geometry Segment Addition Postulate Worksheet

Two Variable System Of Equations With Infinitely Many Solutions

A two-variable system of equations is considered as equations of two lines and they can have infinitely many solutions if these two lines are parallel where they can be expressed as multiples of each other. This is a quick way to spot systems with infinitely many solutions.

For example,

Question 1) How do I Prove Consistent Linear Equations True?

Solution: In order to prove that a given system of linear equations is consistent, you must show that the ranks of the coefficient matrix as well as the corresponding augmented matrix associated with the given system are the same. The easiest way to establish this is to reduce the augmented matrix to a row-echelon form by using elementary row operations on it. It is to be noted that a homogeneous system of equations, i.e. in where the RHS of the equations are equal to 0, is always consistent.

Consistency Of A System Of Linear Equations

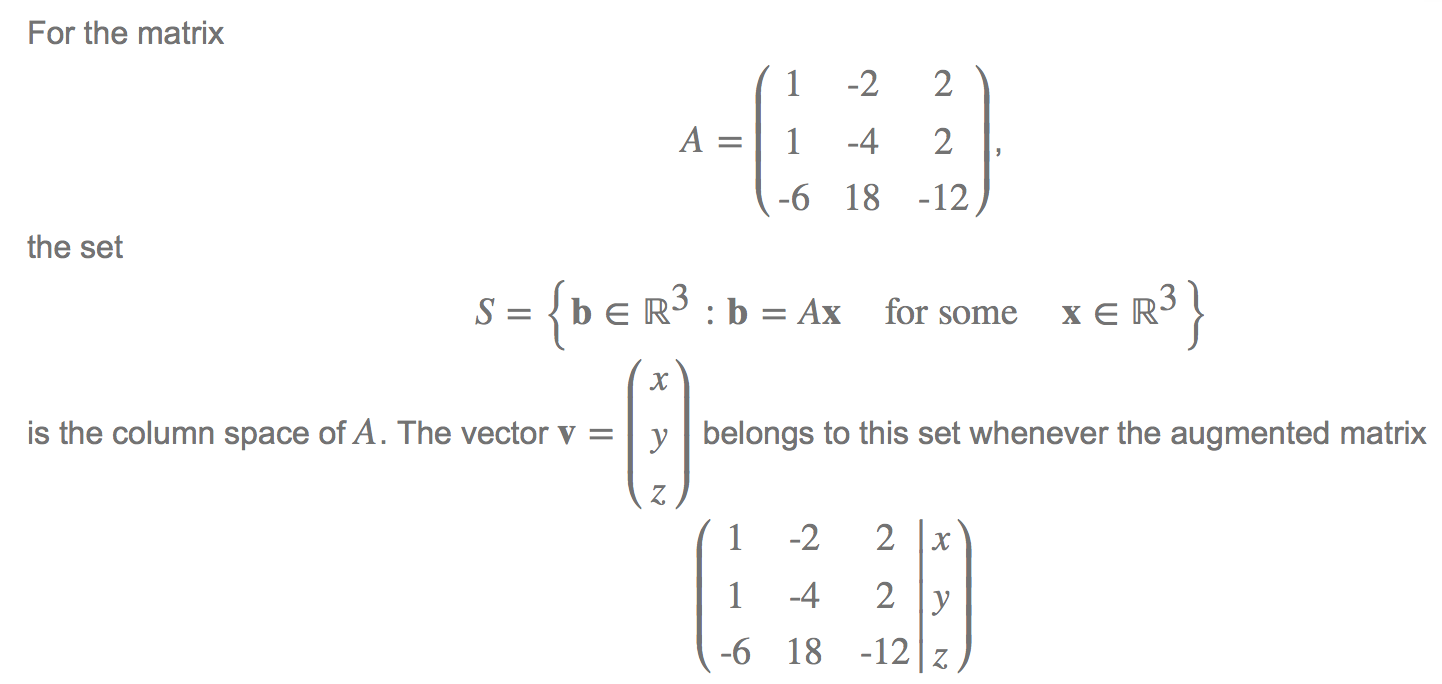
Test the consistency of the system of linear equations

$$\begin 4x-5y+z & =2 \\ 3x+y-2z& = 9 \\ x+4y+z& =5\end$$

We have the system of linear equations given by: $$\begin 4x-5y+z & =2\\ \\ 3x+y-2z& = 9 \\ \\ x+4y+z& =5\end$$

This system can be represented by either of the following augmented coefficient matrices:

$$\begin 4 & -5 & 1 & \mid 2 \\ 3 & 1 & -2 & \mid 9 \\ 1 & 4 & 1 & \mid 5\end\to \quad \text\to \quad \begin 1 & 4 & 1 & \mid 5 \\ 3 & 1 & -2 & \mid 9 \\ 4 & -5 & 1 & \mid 2 \end$$

On the second matrix, we can continue to perform elementary row operations to row reduce the matrix in order to check for consistency. Does this sound familiar?

If we row reduce to obtain a row, e.g., of $$ where $c$ is non-zero, we have an inconsistent system. Else, the system is consistent. Consistency simplyy means: Can all equations simultaneously be true? If so, then the system is consistent. If not, then it is inconsistent. When a system is inconsistent, no solution can possibly exist. When it is consistent, either a unique solution exists, or infinitely many solutions exist.

If you row reduce correctly, to reduced row echelon form, you should obtain the matrix:

$$\begin 1 & 0 & 0 & \mid 2\\ 0 & 1 & 0 & \mid 1 \\ 0 & 0 & 1 & \mid -1 \end$$

Now, what can you say about the system’s consistency?

Don’t Miss: What Math Class Do 11th Graders Take

What Does Inconsistent Systems Mean

Inconsistent equations of linear equations are equations that have no solutions in common. In this system, the lines will be parallel if the equations are graphed on a coordinate plane. Let’s consider an inconsistent equations as x y = 8 and 5x 5y = 25. They dont have any common solutions.

When the lines or planes formed from the systems of equations don’t meet at any point or are not parallel, it gives rise to an inconsistent system.

Sample Mean Of A Normal Random Variable

Suppose one has a sequence of observations from a normal N distribution. To estimate based on the first n observations, one can use the sample mean: Tn = /n. This defines a sequence of estimators, indexed by the sample size n.

From the properties of the normal distribution, we know the sampling distribution of this statistic: Tn is itself normally distributed, with mean and variance 2/n. Equivalently, (

] }\sum _^g\ }\ \operatorname }

• If estimator Tn is defined implicitly, for example as a value that maximizes certain objective function , then a more complicated argument involving stochastic equicontinuity has to be used.

Don’t Miss: Structural Formula Of Ccl4

What Is Inconsistent In Math

inconsistentInconsistentinconsistent

Consistent and Inconsistent Linear Systems. That means that the system of equations they represent has no solution. A system with no solutions is called an inconsistent system.

Also, what does it mean to be consistent? adjective. agreeing or accordant compatible not self-contradictory: His views and actions are consistent. constantly adhering to the same principles, course, form, etc.: a consistent opponent. holding firmly together cohering.

In respect to this, how do you know if a system is independent?

If a consistent system has exactly one solution, it is independent .

What is a consistent system of equations?

In mathematics and in particularly in algebra, a linear or nonlinear system of equations is called as consistent if there is at least one set of values for the unknowns that satisfies each equation in the systemthat is, that when substituted into each of the equations makes each equation hold true as an identity.

Consistent And Inconsistent Equations

In mathematics and particularly in algebra, a linear or nonlinearsystem of equations is called consistent if there is at least one set of values for the unknowns that satisfies each equation in the systemthat is, when substituted into each of the equations, they make each equation hold true as an identity. In contrast, a linear or non linear equation system is called inconsistent if there is no set of values for the unknowns that satisfies all of the equations.

If a system of equations is inconsistent, then it is possible to manipulate and combine the equations in such a way as to obtain contradictory information, such as 2 = 1, or x3 + y3 = 5 andx3 + y3 = 6 .

Both types of equation system, consistent and inconsistent, can be any of overdetermined , underdetermined , or exactly determined.

Also Check: Eoc Fsa Warm Ups Algebra 1 Answers

What Are Dependent Equations

A dependent system of equations is when the same line is written in two different forms so that there are infinite solutions. These two situations occur when trying to solve for a system of equations. … First a system of equations is called Inconsistent if there is no solution because the lines are parallel.

Examples Of Consistent In A Sentence

Rolling StoneThe Story and Its WriterThis Quiet Dust and Other WritingsA Wrinkle in Timeconsistentconsistentconsistentconsistentconsistentconsistentconsistent withconsistent clevelandconsistent Fortuneconsistent CNNconsistent Washington Postconsistent WSJconsistent Anchorage Daily Newsconsistent Dallas Newsconsistent Forbes

These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘consistent.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

Recommended Reading: What Is The Molecular Geometry Of Ccl4

Expressing The Solution Of A System Of Dependent Equations Containing Three Variables

We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same, so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. Or two of the equations could be the same and intersect the third on a line.

What Does K Symbolize

Letter K has the energy of spirituality, charisma, teamwork and relationships. It represents dynamism based on collaboration. Those who have K as the first letter in their name usually rely on intuition and give a lot of importance to their relationships.

Also Check: Geometry Lesson 1.7 Answers

The Existence Of A Unique Solution

A set of linear simultaneous equations may have a unique solution, no solution, or infinitely many solutions.

In a set of linear simultaneous equations, a unique solution exists if and only if, the number of unknowns and the number of equations are equal, all equations are consistent, and there is no linear dependence between any two or more equations, that is, all equations are independent.

In a system of linear simultaneous equations if one or more equations are inconsistent, the system does not have any solution. For example, if in a set of linear simultaneous equations with two equations and two unknowns, one equation is \ and another equation is \, these two equations are inconsistent within the given system. They are inconsistent because if \, then \ must be \, not \. One cannot solve the system of linear simultaneous equations \ and \ as they are inconsistent.

Graphically, the solution of two linear simultaneous equations in two unknowns is equivalent to finding where the lines of the two equations cross. If these two equations are inconsistent, corresponding lines in the Cartesian plane are parallel and will never cross .

In a system of linear simultaneous equations if all equations are consistent, but the number of independent equations is less than the number of unknowns, and/or there exists a linear dependence between two or more equations in the system, there may exists infinitely many solutions that satisfy the system.

Classicists Knew They Were Inconsistent

A donkey in your bedroom?

There are further motivations for paraconsistency beyond those mentioned above.One such motivation is historical: at various times mathematicians worked with theoriesthat they knew at the time to be inconsistent, but were still able to draw meaningfuland useful conclusions. Set theory is one such area. The early calculus, asproposed by Isaac Newton, was another its original formulation required that aquantity be small but non-zero at one stage of a calculation, but then to be equal tozero at a later stage. Despite the inconsistencies, mathematicians still adopted thesetheories and worked with them, drawing useful and sensible conclusions despite the presence of contradictions.

Another motivation is the question of relevance of inference. That is, suppose Ihave proved that the Russell set is and is not a member of itself. Why should it followfrom this that there is a donkey braying loudly in my bedroom? The question ofrelevance is one that has plagued classical logic for a long time, and is one that makesclassical logic a hard pill to swallow to first-time students of logic, who are often toldthat “this is the way it is” in logic. Fortunately for those students, paraconsistencyprovides an alternative.

Read Also: Geometry Dash Practice Mode