What Does Similar Mean In Math

How To Find Range

To find the range in a set of numbers, you must gather your data, organize the data from least to greatest, then subtract the smallest value from the largest value. You can find a range of positive numbers and negative numbers.

Steps for how to calculate range:

For example, if you read a biography, and wrote down how many pages you read each day, you could take the range:

• Monday

To find the range, put the number of pages in order from least to greatest:

Subtract the smallest value from the greatest value:

The range of this data set is 9 s .

Let’s figure the range of the following set of real numbers. Below are five of the lowest-scoring games in NBA history, listed with teams and total game points:

• Washington Capitols vs. Pittsburgh Ironmen 89 points
• Fort Wayne Pistons vs. Minneapolis Lakers 37 points
• Washington Capitols vs. Detroit Falcons 83 points
• Boston Celtics vs. Pittsburgh Ironmen 90 points
• Boston Celtics vs. Washington Capitols 85 points

Go through the three steps to find the range of these five games:

89 points, 37 points, 83 points, 90 points, 85 points

1) Gather the data:

What Does Similar Mean In Math

4.1/5similarsimilarMathematicsmeans

Similarly, you may ask, what is the definition of similar in math?

Please read our Privacy Policy. Two figures that have the same shape are said to be similar. When two figures are similar, the ratios of the lengths of their corresponding sides are equal.

Also Know, what are similar figures examples? Therefore, when we have two similar figures, one is a larger or smaller version of the other. Because of this, when two polygons are similar, their sides are proportional. Being proportional means the ratios of corresponding sides on similar polygons are all equal. For example, consider these two similar rectangles.

Secondly, what does similar mean?

Definition of similar. 1 : having characteristics in common : strictly comparable. 2 : alike in substance or essentials : corresponding no two animal habitats are exactly similar W. H. Dowdeswell. 3 : not differing in shape but only in size or position similar triangles similar polygons.

How do you know if a figure is similar?

Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent , and the ratios of the lengths of their corresponding sides are equal.

What Does Sss Prove

Why do we use congruent instead of equal?

Is congruent to symbol?

Are lines equal or congruent?

What another word for could?

What is a better word for was?

What are the similarities and differences of every individual?

How do you use similarities in a sentence?

What are the similarities between plants and animals?

Can you write cow in 13 letters?

Why do British say H wrong?

What are the 7 letter words?

What is the difference between and in math?

What is this symbol called?

What do three equal lines mean?

In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling , possibly with additional translation, rotation and reflection.

What does similar mean?

What is an example of similar?

Read Also: Segment Addition Postulate Worksheet Pdf Answer Key

Using Range In Real Life

Range is used in real life to make mathematical calculations. Range can be used to calculate the amount of time that has passed, like when calculating your age.

The current year is , and you were born in 2005 . How old are you? Or how much time has passed?

2020

years have passed, so if your 2020 birthday has already passed, then you are 15 years old.

Range is also used in real life to figure out the dispersion of a high school class’ test scores, to determine the price range for a service, and much more.

What Do You Mean By Similarity

When two or more objects or figures appear the same or equal due to their shape, this property is known as a similarity.

When we magnify or demagnify similar figures, they always superimpose each other.

For example, two circles will always superimpose each other because they are similar:

Recommended Reading: Span In Linear Algebra

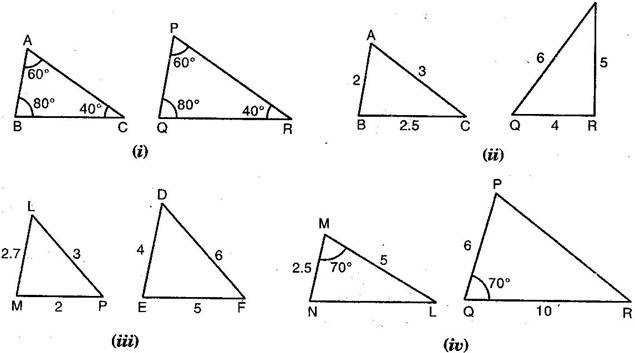
What Are Similar Figures

What does it mean when we say we have 2 similar figures? Similar figures can be thought of as a figure and an enlargement or reduction of that figure, without any distortions. Scale models are one way that the concepts of similar figures is used.

For two polygons to be considered similar, their corresponding angles must have the same measurement and their corresponding sides need to be proportional.

The ratio of the lengths of corresponding sides in two similar figures is the similarity ratio .

Lets start by looking at the parallelograms CATS and BIRD. We can tell they are similar because all the angles are equal and the similarity ratios for the corresponding sides are equal.

$\dfrac=\dfrac = \dfrac$ and $\dfrac=\dfrac= \dfrac$

What Are The Similarities Differences

A similarity is a sameness or alikeness. When you are comparing two things physical objects, ideas, or experiences you often look at their similarities and their differences. Difference is the opposite of similarity. Both squares and rectangles have four sides, that is a similarity between them.

Don’t Miss: Prentice Hall Gold Geometry Teaching Resources Answer Key

What Is The Difference Between Similarity And Congruency

When two figures have the same shape and size, they are congruent. If the figures have the same shape, but not the same size, they are similar.

Look at this pair of coins, they are congruent since having the same shape and the radius of both coins is equal.

Congruent figures are equal in all aspects i.e perimeter, length, and area of congruent figures are always equal.

The major difference is all congruent figures are similar but similar figures are not congruent.

What Does Product Mean In Math

The term product refers to the result of one or more multiplications. For example, the mathematical statement would be read times equals , where. is the product. More generally, it is possible to take the product of many different kinds of mathematical objects, including those that are not numbers.

Recommended Reading: Jonathan Tennant Child Of Rage

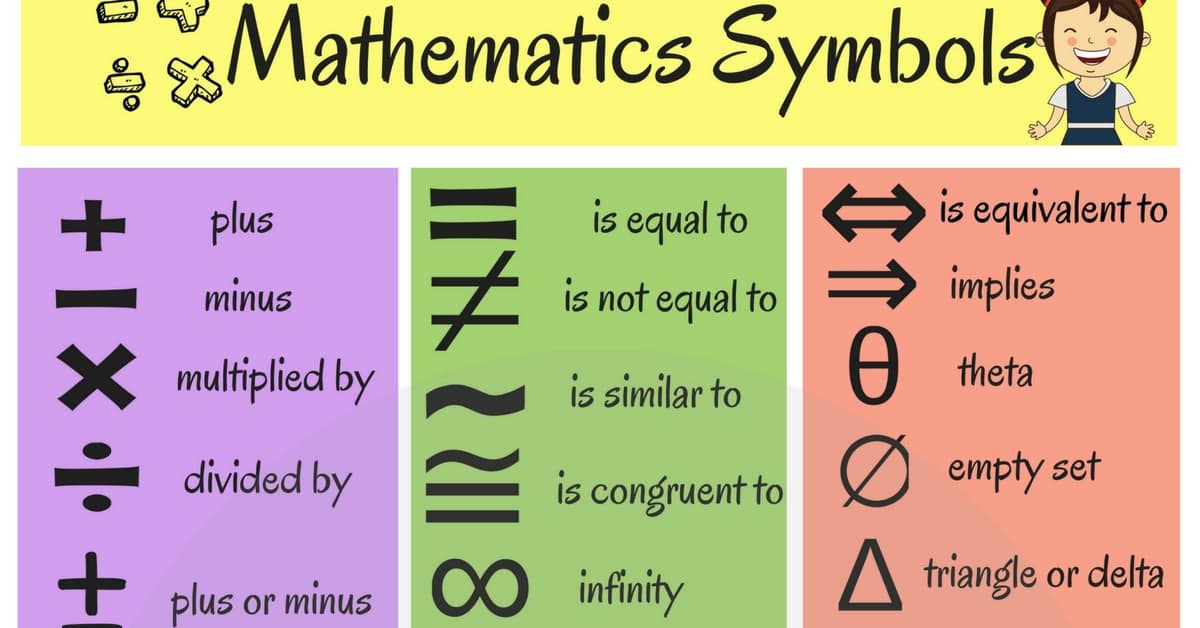
List Of Mathematical Symbols By Subject

The following list of mathematical symbols by subject features a selection of the most common symbols used in modern mathematical notation within formulas, grouped by mathematical topic. As it is impossible to know if a complete list existing today of all symbols used in history is a representation of all ever used in history, as this would necessitate knowing if extant records are of all usages, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units Part 2: Mathematical signs for science and technology.

The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can also be found in the respective linked articles.

< Less Than And > Greater Than

This symbol < means less than, for example 2 < 4 means that 2 is less than 4.

This symbol > means greater than, for example 4 > 2.

These symbols mean less than or equal to and greater than or equal to and are commonly used in algebra. In computer applications < = and > = are used.

These symbols are less common and mean much less than, or much greater than.

Read Also: Redken Chemistry Shot Vs Olaplex

Ratios Of Sides Of Areas And Of Volumes

The ratio between the areas of similar figures is equal to the square of the ratio of corresponding lengths of those figures . The altitudes of similar triangles are in the same ratio as corresponding sides. If a triangle has a side of length b and an altitude drawn to that side of length h then a similar triangle with corresponding side of length kb will have an altitude drawn to that side of length kh. The area of the first triangle is, A = 1/2bh, while the area of the similar triangle will be A = 1/2 = k2A. Similar figures which can be decomposed into similar triangles will have areas related in the same way. The relationship holds for figures that are not rectifiable as well.

The ratio between the volumes of similar figures is equal to the cube of the ratio of corresponding lengths of those figures .

Galileo’s squarecube law concerns similar solids. If the ratio of similitude between the solids is k, then the ratio of surface areas of the solids will be k2, while the ratio of volumes will be k3.

What Is The Application Of Similarity

Some applications of similarity are mentioned below.

• The similarity is widely used in Architecture.
• Solving problems involve height and distance.
• Solving Mathematical problems involving triangles.

• If two angles of two triangles are equal then their third angle is always equal.
• The angle bisector of a triangle always divides the triangle into two similar triangles.
• If two similar triangles have sides in ratio \ then the ratio of their areas will be \

Don’t Miss: Evaluate Homework And Practice Workbook Answers Geometry

Similar Figures: How Is It Useful

The parallelogram FOXZ is similar to CATS and BIRD.

So, what do we know about $m\angle F$?

Well, $\angle F$ corresponds to $\angle B$, so the measurement must be $110^o$.Likewise, $\angle Z$ corresponds to $\angle D$, so the measurement must be $70^o$.

How can we find the value of $\overline$?

The similarity ratio for $\frac=\frac$, since $\overline$ and $\overline$ are corresponding parts. $\overline=n$ is located on the polygon FOXZ, so we would put it across from the $5$ in our ratio, and the corresponding side on CATS is $\overline=2.1$ so we will put it across from the $3$.

$\dfrac=\dfrac =\dfrac$

Now we can solve for the length of $n$ by cross multiplying.$3n = 5\ast2.1$$n = 3.5$

How to find the height of a tree, using similar figures.

Well, we are going to be looking at the ratio of the yardstick to the tree.That ratio is equal to the yard sticks shadow, which is 5 ft., to the trees shadow, which is 35 ft.

$\dfrac=\dfrac =\dfrac$

And that would be equal to the ratio of the height of the yard stick to the height of the tree, which is what we are trying to find out.

$\dfrac=\dfrac =\dfrac$

We can now use equivalent fractions to find the height of the tree.

$\dfrac=\dfrac =\dfrac}$

So, the tree is 21 ft tall.

How To Find The Range Between Two Numbers

The range is typically used to find the dispersion of values in a data set comprising several values. However, you dont need all the other numbers to find the range between two numbers.

Finding the range between two numbers is the same as finding the range of a set of data.

Here you have a set of numbers:

To find the range, you take the greatest value, 10

Now, what if you have only the two numbers 10

The range between these two numbers is the same, 10

Finding the range of a data set is the same as finding the range between two numbers.

Read Also: Geometry Basics Segment Addition Postulate

+ Addition Plus Positive

The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.

The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.

See our page on Addition for more.

How Do You Use The Word Similar

We use similar if two or more things are not entirely the same, or identical if two or more things are exactly the same. We use the patterns similar to and identical to, a similar + noun or a similar + one and an identical + noun or an identical + one. We dont say a same: This colour is similar to that one.

You May Like: Geometry Workbook Answers

Common Mathematical Symbols And Terminology: Maths Glossary

Mathematical symbols and terminology can be confusing and can be a barrier to learning and understanding basic numeracy.

This page complements our numeracy skills pages and provides a quick glossary of common mathematical symbols and terminology with concise definitions.

Are we missing something? Get it touch to let us know.

Or * Or Multiplication

These symbols have the same meaning commonly × is used to mean multiplication when handwritten or used on a calculator 2 × 2, for example.

The symbol * is used in spreadsheets and other computer applications to indicate a multiplication, although * does have other more complex meanings in mathematics.

Less commonly, multiplication may also be symbolised by a dot . or indeed by no symbol at all. For example, if you see a number written outside brackets with no operator , then it should be multiplied by the contents of the brackets: 2 is the same as 2×.

See our page on Multiplication for more.

Recommended Reading: Value Of Amu Degree

What Does Sum Mean In Math

addition. the aggregate of two or more numbers, magnitudes, quantities, or particulars as determined by or as if by the mathematical process of addition: The sum of 6 and 8 is 14. a particular aggregate or total, especially with reference to money: The expenses came to an enormous sum.

Contents

• 14 Whats the weird e in math?

What Does The Long Curly Line Mean

Sorry to sound incredibly ignorant, but I am…at least in math anyway. What does this symbol: $\int$ mean?

• 4Sep 6 ’11 at 0:41
• $\begingroup$It is a double ended fishing pole$\endgroup$

This is the symbol for integration. You may have seen it in Calculus. For example,$$\int x \, dx = \fracx^2 + C$$

• 6$\begingroup$Until you study Calculus, I don’t know how much I can really say about the mathematics. I can give you an example of its practical use, however. Suppose you run a business and had a function that told your profit at any moment in time. The integral can be used to determine your total profit over an interval of time, such as over the course of an entire year.$\endgroup$Sep 6 ’11 at 0:31
• 1Sep 6 ’11 at 0:47

Don’t Miss: Define Consistent In Math

Congruent And Similar Triangles

• Congruent and Similar Triangles

In mathematics, we say that two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection. If the objects also have the same size, they are congruent.

Contents

• Problem Solving – Intermediate

Basic Mathematical Symbols With Name Meaning And Examples

The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.

Don’t Miss: Bridge To Algebra Answers

In General Metric Spaces

In a general metric space, an exact similitude is a functionf from the metric space X into itself that multiplies all distances by the same positive scalarr, called f ‘s contraction factor, so that for any two points x and y we have

d

In topology, a metric space can be constructed by defining a similarity instead of a distance. The similarity is a function such that its value is greater when two points are closer .

The definition of the similarity can vary among authors, depending on which properties are desired. The basic common properties are

). The upper value is often set at 1 .

Note that, in the topological sense used here, a similarity is a kind of measure. This usage is not the same as the similarity transformation of the § In Euclidean space and § In general metric spaces sections of this article.

Using Congruence And Similarity

Knowing the properties of congruence and similarity allows you to use them in proofs. You can establish ratios between corresponding parts of two similar figures, like this:

Here the ratios of width to length are the same:

• 3 cm/5 cm = 1.5 cm/2.5 cm

The ratios of corresponding parts are also the same:

• 5 cm/5 cm = 1.5 cm/3 cm

Using these ratios and the congruence of angles, you know the shapes are similar. They are the same shape and are proportional to each other. You can use similarity in more challenging proofs:

Here the ratios of width to length are the same:

• Given: Right PYH and TON, ST SH
• Prove: PY/NO = PH/NT

• PYT, TON are right s
• ST SH
• PYT TON Right s are all
• STH SHT If two sides of a are , s opposite
• those sides are also .

You May Like: Steve Harvey Twin Daughters