What Does Coordinate Mean In Math

What Is Standard Position Angle

Standard Position: An angle is in standard position if its vertex is located at the origin and one ray is on the positive x-axis. The ray on the x-axis is called the initial side and the other ray is called the terminal side. The angle is measured by the amount of rotation from the initial side to the terminal side.

Coordinate System And Ordered Pairs

A coordinate system is a two-dimensional number line, for example, two perpendicular number lines or axes.

This is a typical coordinate system:

The horizontal axis is called the x-axis and the vertical axis is called the y-axis

The center of the coordinate system is called the origin. The axes intersect when both x and y are zero. The coordinates of the origin are .

An ordered pair contains the coordinates of one point in the coordinate system. A point is named by its ordered pair of the form of . The first number corresponds to the x-coordinate and the second to the y-coordinate.

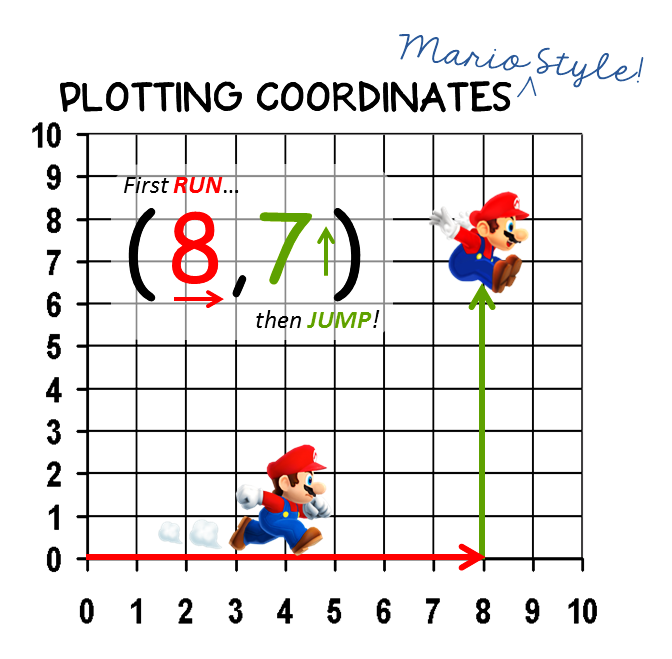
To graph a point, you draw a dot at the coordinates that corresponds to the ordered pair. It’s always a good idea to start at the origin. The x-coordinate tells you how many steps you have to take to the right or left on the x-axis. And the y-coordinate tells you have many steps to move up or down on the y-axis.

Example

The ordered pair is found in the coordinate system when you move 3 steps to the right on the x-axis and 4 steps upwards on the y-axis.

The ordered pair is found in the coordinate system when you move 7 steps to the left on the x-axis and 1 step upwards on the y-axis.

To find out the coordinates of a point in the coordinate system you do the opposite. Begin at the point and follow a vertical line either up or down to the x-axis. There is your x-coordinate. And then do the same but following a horizontal line to find the y-coordinate.

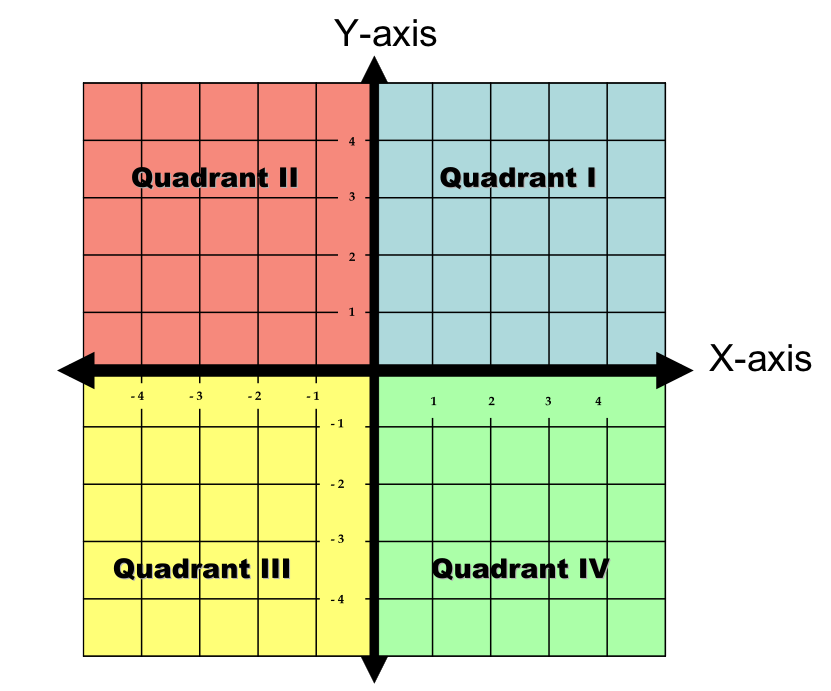
What Are The Quadrants On A Graph

The coordinate axes divide the plane into four regions called quadrants . Students often ask, how are quadrants numbered? A common heuristic is to think of the numbering happening in the same order that we write the letter C. Coordinate plane quadrants are numbered I, II, III, and IV as shown on the grid below.

In Grade 5, students do not usually need to know the numbering system, but should recognize that the appropriate quadrants for ordered pairs can be identified according to the signs of the numbers.

• All points in Quadrant I have two positive coordinates.
• All points in Quadrant II have a negative x-coordinate and a positive y-coordinate.
• All points in Quadrant III have two negative coordinates.
• All points in Quadrant IV have a positive x-coordinate and a negative y-coordinate.

There are many opportunities for discourse that focus on all quadrants of the coordinate plane. Have students brainstorm how someone making an animation or video game might use it, for example. Or show students a variety of graphs taken from different activities and books and have them share what they notice and wonder.

A coordinate plane lets you both visualize and calculate the length of a line segment. Although students do not learn to calculate the length of slanted line segments until learning the Pythagorean Theorem , a four-quadrant plane is enough to find the length of horizontal or vertical line segments.

Recommended Reading: Which Founding Contributors To Psychology Helped Develop Behaviorism

Converting Between Polar And Cartesian Coordinates

The polar coordinates r and can be converted to the Cartesian coordinates x and y by using the trigonometric functions sine and cosine:

x

= 0. =\arctan \left&}x>0\\\arctan \left+\pi &}x<0}y\geq 0\\\arctan \left-\pi &}x<0}y<0\\}&}x=0}y>0\\-}&}x=0}y<0\\}&}x=0}y=0.\end}}

If r is calculated first as above, then this formula for may be stated more simply using the arccosine function:

The equation defining an algebraic curve expressed in polar coordinates is known as a polar equation. In many cases, such an equation can simply be specified by defining r as a function of . The resulting curve then consists of points of the form ,;) and can be regarded as the graph of the polar function r. Note that, in contrast to Cartesian coordinates, the independent variable is the second entry in the ordered pair.

Different forms of symmetry can be deduced from the equation of a polar function r:

• If r = r the curve will be symmetrical about the horizontal ray;
• If r = r it will be symmetric about the vertical ray:
• If r = r it will be rotationally symmetric by clockwise and counterclockwise about the pole.

Because of the circular nature of the polar coordinate system, many curves can be described by a rather simple polar equation, whereas their Cartesian form is much more intricate. Among the best known of these curves are the polar rose, Archimedean spiral, lemniscate, limaçon, and cardioid.

r

The general equation for a circle with a center at (r0,

) \right)}

Watch Along With Our Video To Complete Our Free Translation Worksheet

Watch our free video on how to solve Translations. This video shows how to solve problems that are on our free Translation in Math worksheet that you can get by submitting your email above.

Watch the free Translation in Math video on YouTube here:;Translation in Math

Video Transcript:

This video is about translations in math. You can get the worksheet we use in this video for free by clicking on the link in the description below.

Translation in math refers to when you take a shape or a point on the coordinate grid and you slide it on the coordinate grid. When translating in math your X and your Y coordinates control different ways to translate or slide. The X will control if the figure goes left or right and then the Y will control if it goes down or up. For the figure to go left that means youre going to subtract from the x coordinate, if it was going to go right you have to add to the x coordinate. For it to go down youre going to subtract from the Y and then if its going to go up you will add to the Y.

If you are going to slide this shape, you can slide it right if you add to the X, youll slide it left if you subtract from the X, itll slide up if you add to the Y, and then it will slide down if you subtract from the Y. Most of the time itll be a combination of the change in the x and the y so youll go right and then up or left and then up or left and down. It just all depends on the problem.

Also Check: Exponential Growth And Decay Common Core Algebra 1 Homework Answers

Find Out A General Expression For The Coordinates Of A Point In A Square Based On Certain Distances And An Angle

my problem appears to be a very simple one, but I just can’t seem to figure it out, maybe I am just overlooking something

The problem is defined as the following : I have a square of side L and I have a variable point O inside the square. The distances d1, d2, d3, and d4 are known and the angle between d1 and the horizontal, which I call $\alpha$, is also known. The line segments d1, d3 and d2, d4 make the lines AB and CD respectively, which are perpendicular to each other. My aim is to find the coordinates of the point O when the origin of the 2d plane is the bottom left corner of the square and the X axis is defined by the bottom side of the square, and the Y axis is defined by the left side of the square. In the figure 1, this can be calculated very easily: the coordinate $X=L-d1*cos$ and $Y=L-d4*cos$.

The issue arises when I try and find a general equation to give the coordinates of O. For example in figure 2: $X$ is no longer $L-d1*cos$ but rather is $X=d4*cos$ and $Y$ is no longer $L-d4*cos$ but is $Y=L- d1*sin$. In other words, the expressions for X and Y keep changing based on certain conditions. Ideally, I would want to have a general expression for X and Y regardless of the situation, but I am okay with having a few conditions.

Update: I added another figure to clarify certain doubts.

We are going to introduce a new coordinate system $x’Oy’$ like shown in Fig. 1. If we are able to calculate coordinates of point $P$ in that coordinate systen – we are done because:

In Math The Biggest Question You Will Probably Have Is Mean

In this article well try to describe what this means and how its used in mathematics.

Coordinate is a procedure for translating a set of coordinates. Some examples of coordinate are translating coordinates that are in terms of meters into the ones which are in terms of feet. They comprise translating a single set of coordinates into the following without change, and translating one set of coordinates into a different set of help writing a personal statement coordinates.

Coordinate can be of two types. 1 sort of organize is called in, which stands for the x-direction or the x-axis. The sort of coordinate is y, which stands for its y-axis or the y-direction. So lets discuss these two sorts of coordinate.

With the x and y axes, the coordinate is usually used for instance. The x axis points in the top and the y axis points in the base of the page.

In mathematics coordinate may be utilized to tell the duration of a lineup. Coordinate may also be used to inform the direction that the line is moving, as well as the amount of degrees that it is going around the group, called radians.

Coordinate can be used to measure quantities, paramountessays.com such as pressure, mass, stress, or space. Its possible to use organize to describe the areas of polygons, and the angles between the vertices. This is referred to as surface metric.

The surface of a coordinate space is referred to. What does discriminate imply in this case?

Read Also: What Does Mole Mean In Chemistry

Plotting Points On A Cartesian Plane

A Cartesian is defined by two : the x -axis, which is horizontal, and the y -axis, which is vertical. Using these axes, we can describe any point in the plane using an of numbers.

The Cartesian plane extends infinitely in all directions. To show this, math textbooks usually put arrows at the ends of the axes in their drawings.

The location of a point in the plane is given by its coordinates, a pair of numbers enclosed in parentheses: (

-axis.

Locating A Point On The Coordinate Plane

Now that we are already familiar with the coordinate plane and its parts, let’s discuss how to identify points on a coordinate plane. To locate a point on the coordinate plane, follow the steps given below:

• Step 1: Locate the point.
• Step 2: Find the quadrant by looking at the signs of its X and Y coordinates.
• Step 3: Find the X-coordinate or abscissa of the point by reading the number of units the point is to the right/left of the origin along the X-axis.
• Step 4: Find the Y-coordinate or the ordinate of the point by reading the number of units the point is above/below the origin along the Y-axis.

Let’s look at the coordinate plane examples. Look at the figure shown below.

• Step 1: Observe the blue dot on the coordinate graph.
• Step 2: It is in the second quadrant.
• Step 3: The point is 3 units away from the origin along the negative X-axis.
• Step 4: The point is 2 units away from the origin along the positive Y-axis.

Thus, the point on the graph has coordinates .

Don’t Miss: What Is Cardinal Direction In Geography

Plotting A Point In The Coordinate Plane

In this section, we are going to learn how to plot a point on the coordinate plane. Let’s take the example of point P = . To plot a point in the coordinate plane, follow the steps given below:

• Step 1: Draw two perpendiculars, the X-axis and Y-axis.
• Step 2: Start from the origin. Move 5 units to the right, along the positive X-axis.
• Step 3: Move 6 units up, along the positive Y-axis.
• Step 4: Mark the point of intersection. Mark it as .

Note that P is in the first quadrant. Also, this is known as the positive coordinate plane as the value of both the coordinates for any point in this quadrant will be positive.

Important Points on Coordinate Plane:

• The first quadrant known as the positive coordinates quadrant, is represented by the Roman numeral I.
• The second quadrant is represented by the Roman numeral II.
• The third quadrant is represented by the Roman numeral III.
• The fourth quadrant is represented by the Roman numeral IV.
• The coordinates of any point are enclosed in brackets.

Try to Solve this Challenging Question:

Find out any three points that lie in the positive coordinate plane and for which the abscissa and ordinate are equal and non-negative.

Topics Related to Coordinate Plane

What Is A Coordinate Plane

A coordinate plane is a two-dimensional surface formed by two number lines. It is formed when a horizontal line called the X-axis and a vertical line called the Y-axis intersect at a point called the origin. The numbers on a coordinate grid are used to locate points. A coordinate plane can be used to graph points, lines, and much more. It acts as a map and yields precise directions from one point to another.

Don’t Miss: How To Find Ksp Chemistry

What Does It Mean When A Point Is On The Terminal Side Of An Angle

What does it mean when a point is on the terminal side of an angle? The vertex is always placed at the origin and one ray is always placed on the positive x-axis. This ray is called the initial side of the angle. The other ray is called the terminal side of the angle. The one on the left goes counterclockwise and is defined to be a positive angle.

What does the terminal side of an angle mean?;: a straight line that has been rotated around a point on another line to form an angle measured in a clockwise or counterclockwise direction compare initial side.

What does it mean when a point is on the terminal side?;In this position, the vertex of the angle is on the origin, with a fixed side lying at 3 oclock along the positive x axis. The other side, called the terminal side is the one that can be anywhere and defines the angle.

What does Terminal angle mean?;Positive Angles: Positive angles are angles such that their initial side is the positive x-axis and their terminal side is determined by turning in a counterclockwise direction. Co-Terminal Angles: are angles whose terminal sides fall on the same line.

Read The Short Translation In Math Definition

Translation in Math is when you slide a figure on the Cartesian grid. A Translation in Math can slide a figure left/right or up/down. Translations occur when you add or subtract from either the x or y coordinates. The x coordinate controls if the figures move left or right. The y coordinate controls if the figure moves up or down.

Recommended Reading: What Is Meant By The Process Of Differentiation In Geography

Teaching Quadrant Numbers On A Graph

• ConnectConnect

There are many ways to think fundamentally about the concept of mathematics. One way is to separate the subject into how to write math and how to draw it . A coordinate plane graph lives in the space between writing and drawing mathematics, as the graph can often be described both by written equations and visual shapes.

In the U.S., students in Grades 5 and up typically first learn to perform x– and y-axis graphing on a coordinate plane. Once they are ready for positive and negative integers, often by Grade 6, you can extend graphing to all four quadrants of the coordinate plane.

• Key Standard: Graph points in all four quadrants of the coordinate plane.

How Do You Find An Acute Angle

If the terminal arm is in quadrant 2, do 180 minus the principle angle to find the related acute angle. If the terminal arm is in quadrant 3, do the principle angle minus 180 to find the related acute angle. If the terminal arm is in quadrant 4, do 360 minus the principle angle to find the related acute angle.

Also Check: Geometry Lesson 1.7 Answers

Reading Coordinates On Google Maps

Most GPS devices provide coordinates in the Degrees, Minutes and Seconds format, or most commonly the Decimal Degrees format. The popular Google Maps provides their coordinates in both DMS and DD formats.

The image above shows the location of the Statue of Liberty on Google Maps. The coordinates given for its location are:

40° 41 21.4 N;; 74° 02 40.2 W

This is read as: 40 degrees, 41 minutes, 21.4 seconds north and 74 degrees, 2 minutes, 40.2 seconds west

40.689263; -74.044505

Just to recap, the Decimal Degree coordinates does not have the letters N or S to signify whether the latitude coordinate is above or below the Equator. Neither does it have the letters W nor E to signify whether the longitude coordinate is to the west or east of the Prime Meridian.

This is done through the use of positive and negative numbers. Since the latitude coordinate is positive, the coordinate is above the Equator. Since the longitude coordinate is negative, the coordinate is west of the Prime Meridian.