How To Find The Distance Between Two Points
To find the distance between two points we will use the distance formula:
If you think this is too much effort you can simply use the Distance Calculator from Omni
Calculate The Distance Between Two Points
Were just measuring the distance along each axis, and then using the pythagorean theorem to compute the length of the hypotenuse, which is the imaginary line directly between our two points. It doesnt matter which point is \\) and which is \\). The key idea to take away from this plot is that you only care about the change in x and the change in y. Youll use each of those measurements as the side of a triangle, where the hypotenuse is the distance between the two points.
How to Find the Distance Between Two Points Think of the distance between any two points as a line. The length of this line can be found by using the distance formula: \sqrt^2 + ^2). Take the coordinates of two points you want to find the distance between.
The x-coordinate of the midpoint is half the distance between 45 and 66: 66 45 = 21. Half of 21 is 10½. Add 10½ to 45 to get the midpoints x-coordinate, 55½. The y-coordinate of the midpoint is half the distance between 972 and 191: 972 191 = 781. Half of 781 is 390½. Add 390½ to 191 to get the midpoints y-coordinate, 581½. So the midpoint is .
Distance is an important concept with both theoretical and real-world uses. Calculating distance requires one of two formulas, with the one you use depending on whether youre calculating distance over time or the distance between two points.
Video advice: What is the Distance Formula?
To learn more about Co-ordinate Geometry, enrol in our full course now: https://bit.ly/CoordinateGeometryG10
Faqs On Distance Formula
Any distance formula, as its name suggests, gives the distance . For example, the distance between two points is the length of the line segment connecting them. We use the Pythagoras theorem to derive the formula for distance between two points in a two-dimensional plane which can be extended to find the distance between two points in a three-dimensional plane as well. There are different types of distance formulas in coordinate geometry.
Distance Formula The distance formula is used to determine the distance, d, between two points. If the coordinate
In this free video lesson, you will learn the distance formula and how to use the distance formula to calculate the distance between two points.
The distance of one leg is the difference in the xs. 4-1=3 so that side of the triangle is 3. The distance of the other leg is the difference in the ys. 6-2=4 so that side of the triangle is 4. Now we can use the Pythagorean theorem. The distance formula is actually based off of that:
- Example 1
- Example 2
Video advice: Using Distance Formula to Find Distance Between Two Points!
On this lesson, you will learn how to use the distance formula to find the distance between two points on the coordinate plane!
Don’t Miss: Cca2 Selected Answers
What Is The Formula For Distance In Physics
speedspeedspeedspeed
. Hereof, what is the formula for distance?
The Distance Formula itself is actually derived from the Pythagorean Theorem which is a 2 + b 2 = c 2 + = a2+b2=c2 where c is the longest side of a right triangle and a and b are the other shorter sides .
Secondly, what is the unit for speed? metre per second
Subsequently, one may also ask, what is the formula of displacement in physics?
Introduction to the Displacement and Acceleration EquationIt reads: Displacement equals the original velocity multiplied by time plus one half the acceleration multiplied by the square of time. Here is a sample problem and its solution showing the use of this equation: An object is moving with a velocity of 5.0 m/s.
Why does the distance formula work?
The distance formula is a formula used to find the distance between two distinct points on a plane. The formula was derived from the Pythagorean theorem, which states that for any right triangle, the square of the hypotenuse is equal to the sum of the square of the two legs.
What Is Magnitude Of Force Class 9
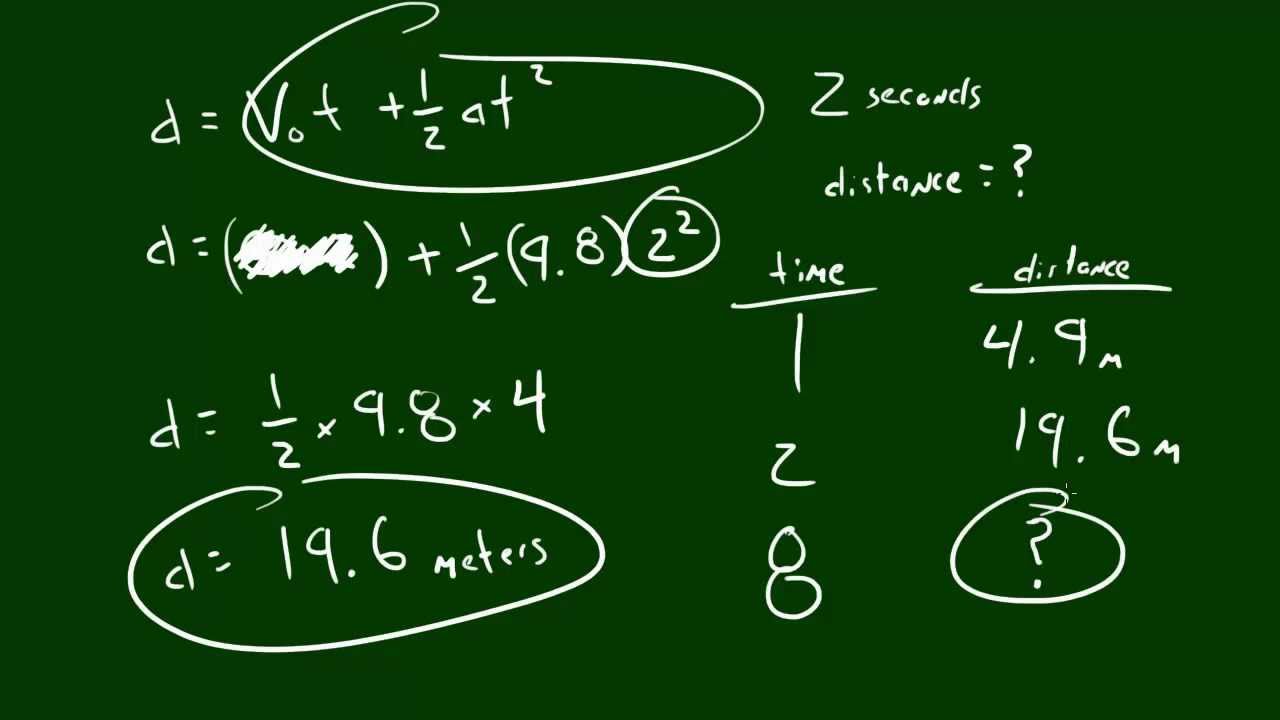
In Physics, the magnitude of force refers to the sum of all the forces that are acting on an object. If all the forces are acting in the same direction, then the magnitude of the force increases. If the forces are acting on an object in different directions, then the magnitude of the force decreases.
Recommended Reading: Answer Key Algebra Nation Section 1 Test Yourself Answers
Distance To A Line And Between 2 Lines
Let’s look at couple examples in 2D space. To calculate the distance between a point and a straight line we could go step by step or we could simply use this ‘handy-dandy’ equation: d = |Ax1 + By1 + C | / where the line is given by Ax+By+C = 0 and the point is defined by .
The only problem here is that a straight line is generally given as y = mx + b so we would need to convert this equation to the previously show form: y = mx + b mx – y + b = 0 so we can see that A = m, B = -1 and C = b. This leaves the previous equation with the following values: d = |mx1 -y1 + b | / .
For the distance between 2 lines, we just need to compute the length of the segment that goes from one to the other and is perpendicular to both. Once again, there is a simple formula to help us: d= |C2-C1|/ if the lines are A1 x+B1 y+C1 = 0 and A2x+B2y+C2 = 0. We can also convert to slope intercept for and obtain: d= |b2-b1|/ for lines y = m1x + b1 and y = m2x + b2.
Notice that both line needs to be parallel since otherwise the would touch at some point and their distance would then be d = 0. That’s the reason the formulas omit most of the subscripts since for parallel lines: A1 = A2 = A and B1 = B2 = B while in slope intercept form parallel lines are those for which m1 = m2 = m
How Is The Power Of The Lens Affected By Its Curvature
The answer to this question is similar to the one described in terms of Power Dependency. The Power of the Lens is the level at which the Lens meets or separates the light source from it. Now, this combination or separation will depend on how much the Lens is curved. A highly curved Lens means that it will have a high angle of separation or separation to give light to the event. Similarly, a slightly curved Lens means that it will have little or no contact to give light. In this way, the Power of the Lens depends on the angle of the Lens.
You May Like: Kuta Software Infinite Algebra 2 Operations With Complex Numbers
What Is The Formula Of Distance And Displacement
formula of distance=speed multiplied by time. formula of displacement=final position-initial position.
What is distance traveled? Distance traveled is the total length of the path traveled between two positions. Distance traveled is not a vector. It has no direction and, thus, no negative sign. For example, the distance the professor walks is 2.0 m 2.0 text 2.
What is distance give two example?
Distance is defined as the amount of space between two things or the state of being far apart. An example of distance is five feet between two tables. An example of distance is the difference between two sides of an issue.
How can you measure distance? Measure distance between points
Solved Example On Distance Formula
Example 1
Suppose a dog runs from one end of the street to another end of the street and the street is 80.0 meters across. Moreover, the takes 16.0 seconds to cross reach the end of the street. Now, calculate the speed of the dog?
Solution:
As we discussed earlier the distance formula can be interchanged to find the speed of the body or object.So, the distance and time is present in the question that is 80.0 m and 16.0 s respectively. Now, put these values in the question
Speed = \
S = \
S = 5.0 m/s
So, the speed of the dog will be 5 m/s.
Example 2
Now, in another situation, a golf cart driver is driving the golf cart that has a maximum speed of 27.0 km/h. Furthermore, the driver drives the car for 10.0 minutes. So, calculate the distance covered by the golf cart with its top speed in 10.0 minutes?
Solution:
For solving this problem first of all we need to convert the speed from km/h to m/s and time from minutes to seconds.Calculating speed
s = 27.0 km/h
s = 27.0 ×\ × \ × \ × \
So, s = 7.50 m/s
Also Check: What Does Capital G Mean In Physics
Why Is Delta Used As A Variable In Math
Tap to check for your leaks. A variable is something that stands in place of a number or set of numbers. Delta can be a variable. It is the 4th letter of Greek alphabet and since early mathematics was much tied to classical Greece, it’s lettering has long been used in mathematics. Why? No good reason, really.
What Is Echo Formula
4/5echoabout it here
Echo. In audio signal processing and acoustics, echo is a reflection of sound that arrives at the listener with a delay after the direct sound. The delay is directly proportional to the distance of the reflecting surface from the source and the listener.
Likewise, what are the uses of Echo? Echoes are used by bats, dolphins and fisherman to detect an object / obstruction. They are also used in SONAR and RADAR to detect an obstacle.
Additionally, what is Echo how is it produced?
Sound Waves and EchoesThis called an echo. The sound waves left your mouth, traveled through the air, hit a hard surface, such as a wall, and then bounced back again, causing you to hear the sound again. An echo is made by sound waves bouncing off a hard surface.
How can you calculate the minimum distance for Echo?
1, we get: d=v*0.1/2 or, d= v*0.05 Now if we are trying to hear echo in air, then v is approximately 343m/s. So the minimum distance required to hear an echo in air is achieved by: d=343*0.05 or, d=17.15 Therefore to hear echo in air at room temperature, the minimum distance is 17.15m.
Recommended Reading: Lewis Dot Structure For Ccl4
How Much Was 10 Cents 1950
Additionally What is distance in physics with example? The distance of an object can be defined as the complete path travelled by an object. For example. if a car travels east for 5 km and takes a turn to travel north for another 8 km, the total distance travelled by car shall be 13 km.
What is distance in physics class 11? Distance is the actual path length traveled by an object in the given interval of time during the motion.
Distances Between Sets And Between A Point And A Set

Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a low Earth orbit, the first tends to be quoted , otherwise, e.g. for the EarthâMoon distance, the latter.
There are two common definitions for the distance between two non-empty subsets of a given metric space:
- One version of distance between two non-empty sets is the infimum of the distances between any two of their respective points, which is the everyday meaning of the word, i.e.
- d . d.}
- This is a symmetric premetric. On a collection of sets of which some touch or overlap each other, it is not “separating”, because the distance between two different but touching or overlapping sets is zero. Also it is not hemimetric, i.e., the triangle inequality does not hold, except in special cases. Therefore only in special cases this distance makes a collection of sets a metric space.
- The Hausdorff distance is the larger of two values, one being the supremum, for a point ranging over one set, of the infimum, for a second point ranging over the other set, of the distance between the points, and the other value being likewise defined but with the roles of the two sets swapped. This distance makes the set of non-empty compact subsets of a metric space itself a metric space.
Also Check: Algebra 1 Eoc Fsa Practice Test No Calculator Portion Answers
What Is The Distance In Physics
Distance is defined to be the magnitude or size of displacement between two positions. Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions. Distance traveled is not a vector.
Finding The Distance Between Two Points
Recommended Reading: Common Core Worksheets 2nd Grade
How To Find The Distance Using Our Distance Calculator
As we have mentioned before, distance can mean many things, which is why we have provided a few different options for you in this calculator. You can calculate the distance between a point and a straight line, the distance between two straight lines , or the distance between points in space. When it comes to calculating the distances between two point, you have the option of doing so in 1, 2, 3, or 4 dimensions. I know, I know, 4 dimensions sounds scary, but you don’t need to use that option. And you can always learn more about it by reading some niceresources and playing around with the calculator. We promise it won’t break the Internet or the universe.
We have also added the possibility for you to define 3 different points in space, from which you will obtain the 3 pairs of distances between them, so, if you have more than two points, this will save you time. The number of dimensions you are working in will determine the number of coordinates that describe a point, which is why, as you increase the number of dimensions, the calculator will ask for more input values.
Even though using the calculator is very straightforward, we still decided to include a step-by-step solution. This way you can get acquainted with the distance formula and how to use it . Now let’s take a look at a practical example: How to find the distance between two points in 2-D.
Examples Using Time Formula
Let us solve some interesting problems using the time formula.
Example 1: A train covered a distance of 120 km at a speed of 60km/hr. Using the time formula calculate the time taken by the train in covering the distance.
Solution:
To find the time taken by the train.Given:Distance covered by a train = 120km Speed of a train = 60 km/hrUsing Formula of Time,= 120/60= 2 hr
Answer: The time taken by the train to cover 120 km at the speed of 60km/hr is 2 hours.
Example 2: A cyclist covers 20 km at a speed of 5km/hr. Use the time formula and find the time taken by the cyclist in covering the distance.
Solution:
To find the time taken by the cyclist.Distance covered by a cyclist = 20 kmSpeed of the cyclist = 5km/hr.Using Formula of Time,= 20/5= 4 hr
Answer: The time taken by the cyclist to cover 20 km at 5km/hr is 4 hours.
Example 3: Using the time formula calculate the time taken by a person in covering a distance of 400 kilometers at speed of 20 kilometers per hour?
Solution:
The formula for time is Distance = 400 kilometers
Answer: Thus the person covered a distance of 400 kilometers in 20 hours.
Also Check: Example Of Density In Human Geography