The Y Intercept From Standard Form
Standard form is y = ax2 + bx + c. When you plug in a zero for x, the only term that remains a non-zero term is c, except when the y intercept is at the origin. So, the logical thing to do, from standard form, is to recognize that c is the y coordinate of the y intercept.
Lets see an example. Consider y = x2 3x + 3. If you plugged in a zero for x, youd get 2 3 + 3, which simplifies to just 3. The y intercept is NOT 3. Intercepts are coordinates, locations on a graph. There are a lot of important coordinates with quadratic equations, so dont confuse yourself. Be sure to write .
The issue with this comes when you see quadratic equations written in Vertex Form. There, the last number you see is NOT the y coordinate of the y intercept at all! Lets see how that works.
How To Find X And Y Intercepts
Consider a straight line equation Ax + By = C.
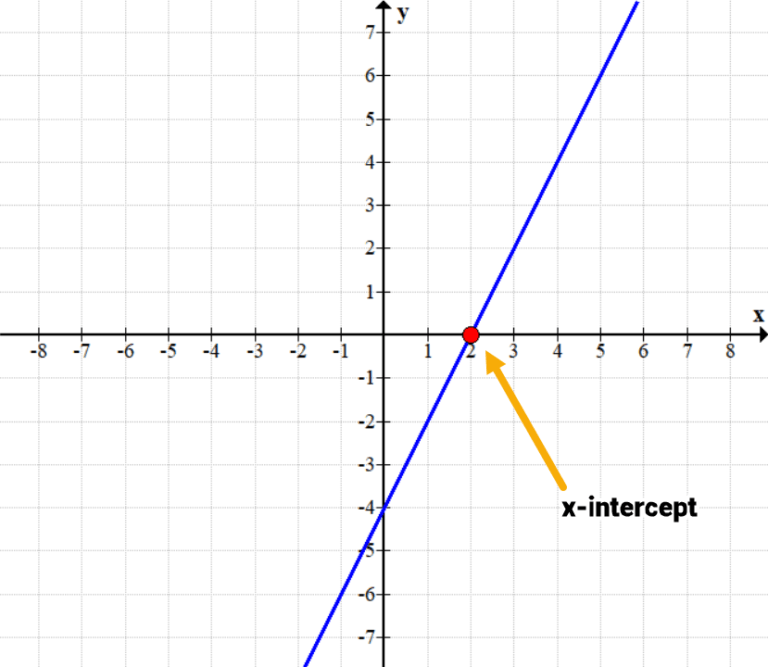
To find the x-intercept, substitute y = 0 and solve for x.
To find the y-intercept, substitute x =0 and solve for y.
Example: Let us assume the straight-line equation 5x +2y =10
To find x-intercept:
Substitute y=0 in the given equation
5x + 2 = 10
The formula of the line formed by the two points is given by:
y-y1/y2-y1 = x-x1/x2-x1
Say, P = and Q = are the two points of the line which cuts the x-axis and y-axis, relative to the origin. Then the formula becomes:
=> y 0 / b 0 = x a/ 0 a
=> y/b = x/-a a/-a
Hence, proved.
How To Find The Y Intercept Of A Quadratic In Standard Form
Standard form is perhaps the most common and the easiest to understand. Simply plug zero in as the value of x in the standard quadratic equation and solve. Here’s an example.
Let’s say your function is y = 5×2 + 11x + 72. Assign “0” as your x value and solve.
y = 52 + 11 + 72 = 72
You would then write the answer in the coordinate form of .
Also Check: Age Word Problems
Examples Of How To Find The X And Y
Example 1: From the graph, describe the x and y-intercepts using point notation.
The graph crosses the x-axis at x= 1 and x= 3, therefore, we can write the x-intercepts as points and .
Similarly, the graph crosses the y-axis at y=3. Its y-intercept can be written as the point .
Example 2: Find the x and y-intercepts of the line y = 2x + 4.
To find the x-intercepts algebraically, we let y=0 in the equation and then solve for values of x. In the same manner, to find for y-intercepts algebraically, we let x=0 in the equation and then solve for y.
Heres the graph to verify that our answers are correct.
Example 3: Find the x and y-intercepts of the quadratic equation y = x2 2x 3.
The graph of this quadratic equation is a parabola. We expect it to have a U shape where it would either open up or down.
To solve for the x-intercept of this problem, you will factor a simple trinomial. Then you set each binomial factor equal to zero and solve for x.
Our solved values for both x and y-intercepts match with the graphical solution.
Example 4: Find the x and y-intercepts of the quadratic equation y = 3x2 + 1.
This is an example where the graph of the equation has a y-intercept but without an x-intercept.
- Lets find the y-intercept first because its extremely easy! Plug in x = 0 then solve for y.
- Now for the x-intercept. Plug in y = 0, and solve for x.
The square root of a negative number is imaginary. This suggests that this equation does not have an x-intercept!
ABOUT
A Guide For How To Find The Y Intercept Of A Line
When Finding the Y-Intercept from a Graph and Table, you are searching for the point of intersection between the equation and the y-axis. When finding the Y-Intercept from a Graph, you should find where the line from the equation crosses the y-axis. The point where the equation crosses the y-axis is the Y-Intercept. When finding the Y-Intercept from a Table, you have to discover the y-value from the table when the x-value is equivalent to zero. When the table has a x-value of zero in it, you just check the y-value. When the table does not have a x-value of zero, you should use the slope to go in reverse to discover the x-value of zero.
Read Also: What Is Figure Ground Perception Psychology
What Is Y On A Graph
Drawing a Coordinate Graph The numbers on a coordinate grid are used to locate points. Each point can be identified by an ordered pair of numbers that is, a number on the x-axis called an x-coordinate, and a number on the y -axis called a y -coordinate.
What Is An Intercept
I have always taught my students that the $y$-intercept of a line is the $y$-coordinate of the point of intersection of a line with the $y$-axis, that is, for the line given by the equation $y=mx+y_0$, the $y$-intercept is $y_0$. I emphasize that that the $y$-intercept is the number$y_0$ and not the point$$.
But I was quite surprised when I recently looked at the Wikipedia and WolframMathWorld entries for $y$-intercept because these define the intercept as a point and not as a number .
Further investigation yielded inconsistencies: the Wikipedia entry for “Line ” states that in the equation $y=mx+b$, “$b$ is the y-intercept of the line” the Wolfram MathWorld entry for “Line” states that “The line with $y$-intercept $b$ and slope $m$ is given by the slope-intercept form $y=mx+b$.
Edit made on February 21, 2021
According to the Dictionary of Analysis, Calculus, and Differential Equations ,
intercept The point where a curve or graph of a function in $\mathbf R^n$ crosses one of theaxes. For the graph of $y=f$ in $\mathbf R^2$, the $y$-intercept is the point $)$ and the $x$-intercepts are the points $)$ such that $f=0$.
Unfortunately, the book does not consistently use that definition.
slope-intercept equation of line An equation of the form $y=mx+b$, for a straight line in $\mathbf R^2$. Here $m$ is the slope of the line and $b$ is the $y$-intercept that is, $y=b$, when $x=0$.
Thus, even though the book defines an intercept as a point, it uses the term to denote a number.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Determining And Interpreting Intercepts From A Graph
An intercept of any function is a point where the graph of the function crosses, or intercepts, the x-axis or y-axis.
Because there are two axes on a coordinate plane, there can be a x-intercept, which is the point where the graph crosses the x-axis , or a y-intercept, which is the point where the graph crosses the y-axis or both.
When the linear function is used to represent a real-world situation, the intercepts have significant meaning in the context of the problem.
Pause and Reflect
How can you distinguish between the x-intercept and the y-intercept from a graph?
Practice
Interpret both the x– and y-intercepts in the relationships shown in the graphs below.
1. The graph shown below represents the number of tickets that a theater must sell in order to generate $350 in revenue from ticket sales.
2. A hiker is hiking down a canyon toward the canyon floor. On the graph below you can see her height above the canyon floor as a function of time.
Can A Parabola Have No Y
All parabolas are vaguely U shaped and they will have a highest or lowest point that is called the vertex. Parabolas may open up or down and may or may not have x -intercepts and they will always have a single y -intercept. The dashed line with each of these parabolas is called the axis of symmetry.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
How To Find The Y Intercept In A Quadratic Equation
Quadratic equations are mathematical functions where one of the x variables is squared, or taken to the second power like this: x2. When these functions are graphed, they create a parabola which looks like a curved “U” shape on the graph. This is why a quadratic equation is sometimes called a parabola equation.
Two important values concerning these mathematical functions are the x-intercept and the y-intercept. The x-intercept indicates where the parabola graph of that function crosses the x axis. There can be one or two x intercepts for a single quadratic equations.
The y-intercept indicates where the parabola crosses the y axis. There is only one y intercept for each quadratic equation.
What Is The Y
The standard form of such an equation is Ax + By + C = 0 or Ax + By = C. When you rearrange this equation to get y by itself on the left side, it takes the form y = mx +b. This is called slope intercept form because m is equal to the slope of the line, and b is the value of y when x = 0, which makes it the y intercept.
Don’t Miss: Geometry Assignment Find The Length Indicated Answer Key
Determining And Interpreting Intercepts From A Table
You can also use a table of values to determine and interpret the intercepts of a function. The graph below represents the relationship between the floor number and the amount of time that Senedra has been in an elevator. Senedra is in an office building in Europe, where the ground floor is labeled “Floor 0” and the next floor up is labeled “Floor 1.”
Copy and paste the table below into your notes. Use the elevator graph above to complete the table. Click on the plus sign to check your answers.
Use your graph and table to answer the following questions.
- What are the coordinates of the y-intercept?
- What does the y-intercept represent in this situation?
- What are the coordinates of the x-intercept?
- What does the x-intercept represent in this situation?
Practice
Interpret both the x– and y-intercepts in the relationships shown in the tables below.
1. The table below shows the distance remaining in a bus trip from Houston to Dallas as a function of time. How far is it in miles from Houston to Dallas? How many hours will the trip take?
| Time in Hours, x |
|---|
y-intercept:
Practice: Slope-Intercept Form
In the problems below, drag the mathematical steps of solving the equation into the correct descending order in each row. Use the completed solutions to look for patterns in how you can determine the x-intercept and y-intercept for a linear equation that is given in slope-intercept form.
Practice: Standard Form
Slope Intercept Form Formula
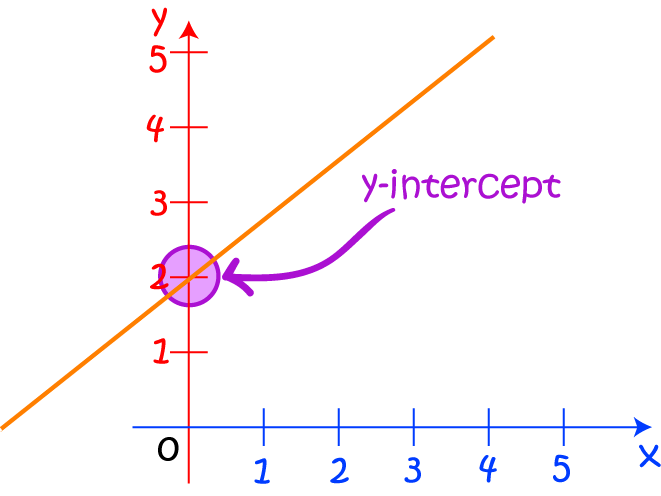
For the equation, y = mx + b, m is the slope of the line that is multiplied by x and b is the y-intercept or we can say the point where the line will cross the vertical y-axis. This is a sensible equation that can also be named as the slope-intercept form. Designing a graph from this equation is easy especially when values are simpler. In this post, we will discuss almost every aspect of the graph and formulas for x and y-intercepts. Also, you would know the real-world application of slope intercepts and how to model the equations in practical terms.
The values used in formula are as follows:m is the slope of the line.b is the y-intercept of the line.
This is not possible to understand graphs your own. You need a teacher who can guide you and lots of practice to reach the conclusion. You should know how graphs are designed when the value of x-variable increases and the value of y-variable increases over time. The concept can be more useful when you consider the same for the real-world problems.
Don’t Miss: Illest Road Trip Of All Time
How To Find The Y Intercept Of A Table Example
Video Explanation Including The Y Intercept In Math Definition
Watch our free video on how to solve Finding Y Intercept. This video shows how to solve problems that are on our free Finding Y Intercept worksheet that you can get by submitting your email above.
Watch the free Finding Y Intercept video on YouTube here: How to find Y Intercept
Video Transcript:
This video is about how to find y-intercept. You can get the worksheet used in this video for free by clicking on the link in the description below.
The first part of our worksheet is about how to find y-intercept from a graph. In order to find the y-intercept by looking at a graph you have to look at where your line crosses the y axis. If we wanted to we could go ahead and label our graph. We know that this is the y axis and we know that this is the x axis. The y axis is always a vertical axis and the x axis is always the horizontal axis. What you are looking for is youre looking for the spot where your line crosses the y axis, youre trying to find exactly where your linear equation will cross the y axis.
If you look at our first example here the line crosses the y axis right here. When y equals 1 that means our y-intercept has to be 1 and thats our solution.
Recommended Reading: Eoc Fsa Practice Test Algebra 2 Calculator Portion
Different Forms Of Quadratic Equations
Quadratic equations come in three general forms. These are the standard form, vertex form and factored form.
Standard form looks like this:
y = ax2 + bx + c where a, b and c are known constants and x and y are variables.
Vertex form looks like this:
y = a2 + c where a, b and c are known constants and x and y are variables.
Factored form looks like this:
y = a where a is a known constant, r1 and r2 are “roots” of the equation , and x and y are variables.
Each of the forms looks drastically different, but the method for finding the y intercept of a quadratic equation is the same despite the various forms.
The Y Intercept From Vertex Form
Vertex form is f = a2 + k. Remember, the x coordinate of the y intercept is always zero. Thats why we plug in a zero for x. Lets see how this work with vertex form.
Since there is always one y intercept, and it is simpler to find than the vertex or x intercepts, it is a good idea to start with it. So, find the y intercept first if youre asked to graph. The next thing youll find is the vertex, which we will discuss in the upcoming section.
Consider making your next Amazon purchase using our Affiliate Link. You get the same prices, service and shipping at no extra cost, but a small portion of your purchase price will go to help maintaining this site!
Recommended Reading: What Is The Molecular Geometry Of Ccl4
The Short Answer To: What Is The Y Intercept
When Finding the Y-Intercept from a Graph and Table you are looking for the point of intersection between the equation and the y-axis. When finding the Y-Intercept from a Graph, all you have to do is find where the line from the equation crosses the y-axis. The point at which the equation crosses the y-axis is the Y-Intercept. When finding the Y-Intercept from a Table, you need to find the y-value from the table when the x-value is equal to zero. If the table already has a x-value of zero in it, then all you need to do is look at the y-value. If the table is missing an x-value of zero, then you must use the rate of change to go backwards or forwards to find the x-value of zero. Always be sure to follow the pattern that is shown in the table.
Common Core Standard: 8.F.B.4
How To Find Y
We have derived the formulas to find the y-intercept of a line where the equation of the straight line is in different forms. In fact, we do not need to apply any of these formulas to find the y-intercept of a straight line. The y-intercept of the polynomial function of the form \ is just its constant term \ \\).
We just substitute x=0 in the equation of the line and solve for y. Then the corresponding y intercept is y or .
| Equation of Line | |
|---|---|
| y=2-3=-3 | -3 |
The y-intercept of a function can be easily found by graphing it using the graphing calculator and locating the point where the graph cuts the y-axis. A function has only one y-intercept because otherwise, it fails the vertical line test. The y– intercept of the second equation of the table is shown in the graph below.
Also Check: Holt Geometry Chapter 7 Test Answer Key
What Is The Y Intercept Of A Quadratic Function
The y-intercept is where the parabola of a function crosses the y axis. Another way to define the y-intercept is the value of y when x is equal to zero.
Because the y intercept is a point on a graph, you’ll usually write it in point/coordinate form. For example, let’s say your y value of the y intercept is 6.5. You would write the y intercept as .